XLA TPU এর ভেক্টর রেজিস্টারের দ্বি-মাত্রিক প্রকৃতির কারণে বিভিন্ন ধরণের টাইল-ভিত্তিক ফর্ম্যাট ব্যবহার করে।
টাইল্ড ফর্ম্যাট
একটি টাইল্ড ফর্ম্যাট একটি আকৃতিকে টাইলস (সাধারণত 1D বা 2D) এ ভেঙে দেয়। টাইলস মেমোরিতে মেজর থেকে মাইনর ক্রমে (সারি মেজর লেআউট) সাজানো থাকে। একটি টাইলের মধ্যে, উপাদানগুলি মেজর থেকে মাইনর ক্রমেও সাজানো থাকে।
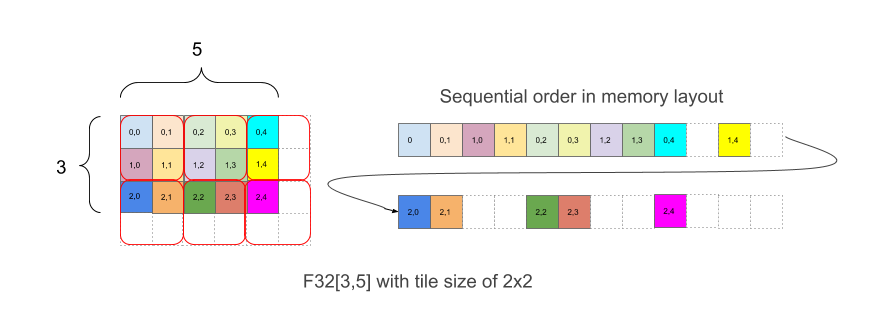
চিত্র ১
চিত্র ১-এ দেখানো হয়েছে কিভাবে একটি অ্যারে F32[3,5] মেমরিতে 2x2 টাইলিং সহ বিন্যস্ত করা হয়েছে। এই লেআউট সহ একটি আকৃতি F32[3,5]{1,0:T(2,2)} হিসাবে লেখা হয়, যেখানে 1,0 মাত্রার ভৌত ক্রম (লেআউটে minor_to_major ক্ষেত্র) এর সাথে সম্পর্কিত, যখন কোলনের পরে (2,2) 2x2 টাইলিং দ্বারা ভৌত মাত্রার টাইলিং নির্দেশ করে।
স্বজ্ঞাতভাবে, আকৃতিটি ঢেকে রাখার জন্য টাইলস বিছিয়ে দেওয়া হয় এবং তারপরে প্রতিটি টাইলের মধ্যে, উপাদানগুলি টাইলিং ছাড়াই বিছিয়ে দেওয়া হয়, যেমন উপরের উদাহরণে, যেখানে উদাহরণের ডান অংশটি মেমরিতে লেআউটটি দেখায়, যার মধ্যে সাদা প্যাডিং উপাদানগুলিও রয়েছে যা সম্পূর্ণ 2x2 টাইলস রাখার জন্য যোগ করা হয় যদিও মূল অ্যারের সীমানা সমান নয়।
প্যাডিংয়ের অতিরিক্ত উপাদানগুলিতে কোনও নির্দিষ্ট মান থাকা প্রয়োজন হয় না।
আকৃতি এবং টাইলের ভিত্তিতে টাইলিং করার জন্য রৈখিক সূচক সূত্র
টাইলিং ছাড়াই, d=(d n , d n-1 , ... , d 1 ) অ্যারে সীমানা সহ একটি অ্যারেতে (d1 হল সবচেয়ে গৌণ মাত্রা) একটি উপাদান e=(e n , e n-1 , ... , e 1 ) অবস্থানে মেজর থেকে গৌণ ক্রম অনুসারে সাজানো হয়:
রৈখিক_সূচক(ঙ, ঘ)
= রৈখিক_সূচক((e n , e n-1 , ..., e 1 ), (d n , d n-1 , ..., d 1 ))
= e n d n-1 ...d 1 + e n-1 d n-2 ...d 1 + ... + e 1
এই নথিতে স্বরলিপির সরলতার জন্য আমরা ধরে নিচ্ছি যে একটি টাইলের অ্যারের মতো একই সংখ্যক মাত্রা রয়েছে। XLA-এর টাইলিং বাস্তবায়নে, প্রাথমিক সর্বাধিক-প্রধান মাত্রাগুলিকে অপরিবর্তিত রেখে এবং কেবলমাত্র সবচেয়ে ছোট মাত্রাগুলিতে টাইলিং প্রয়োগ করে এটি কম মাত্রা সহ টাইলিংগুলিতে সাধারণীকরণ করা হয়েছে, যাতে নির্দিষ্ট করা টাইলিংটি টাইলিং করা আকৃতির ভৌত মাত্রার একটি প্রত্যয় উল্লেখ করে।
যখন আকারের টাইলিং (t n , t n-1 , ..., t 1 ) ব্যবহার করা হয়, তখন সূচক (e n , e n-1 , ..., e 1 ) সহ অ্যারের একটি উপাদান চূড়ান্ত বিন্যাসে এই অবস্থানে ম্যাপ করা হয়:
লিনিয়ার_ইনডেক্স_উইথ_টাইল(e, d, t)
= linear_index((⌊e/t⌋, e mod t), (⌈d/t⌉, t)) (পাটিগণিত হল উপাদান অনুসারে, (a,b) হল সংযোজন)
= লিনিয়ার_ইনডেক্স((⌊ e n /t n ⌋, ..., ⌊e 1 /t 1 ⌋, e n mod t n , ..., e 1 mod t 1 ), (⌈d n /t n ⌉, ..., ⌈d 1 /t 1 ⌉, t n , t n-1 , ..., t 1 ))
= রৈখিক_সূচক((⌊e n /t n ⌋, ... , ⌊e 1 /t 1 ⌋), (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉))∙t n t n-1 ...t 1 + রৈখিক_সূচক((e n mod t n , ... , e 1 mod t 1 ), (t n , t n-1 , ... , t 1 ))
লেআউটটিকে দুটি অংশ হিসেবে ভাবা যেতে পারে: (⌊e n /t n ⌋, ... , ⌊e 1 /t 1 ⌋), যা আকারের (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉) টাইলগুলির একটি অ্যারের একটি টাইল সূচকের সাথে সঙ্গতিপূর্ণ, এবং (en n mod t n , ... , e 1 mod t 1 ), যা একটি অভ্যন্তরীণ-টাইল সূচকের সাথে সঙ্গতিপূর্ণ। সিল ফাংশনটি ⌈d i /t i ⌉ এ প্রদর্শিত হয় কারণ যদি টাইলগুলি বৃহত্তর অ্যারের সীমা অতিক্রম করে, তাহলে চিত্র 1 এর মতো প্যাডিং সন্নিবেশ করা হয়। টাইলগুলির মধ্যে থাকা টাইল এবং উপাদানগুলি উভয়ই টাইলিং ছাড়াই পুনরাবৃত্তভাবে সাজানো হয়েছে।
চিত্র ১-এর উদাহরণের জন্য, (২,৩) উপাদানের টাইল সূচক (১,১) এবং (১,১,০,১) এর সম্মিলিত স্থানাঙ্ক ভেক্টরের জন্য অভ্যন্তরীণ টাইল সূচক (০,১) রয়েছে। টাইল সূচকগুলির সীমা (২,৩) রয়েছে এবং (২,৩,২,২) এর সম্মিলিত ভেক্টরের জন্য টাইল নিজেই (২,২)। লজিক্যাল আকারে সূচক (২,৩) সহ উপাদানের টাইল সহ রৈখিক সূচক হল
লিনিয়ার_ইনডেক্স_উইথ_টাইল((২,৩), (৩,৫), (২,২))
= রৈখিক_সূচক((১,১,০,১), (২,৩,২,২))
= রৈখিক_সূচক((১,১), (২,৩)) ∙ ২ ∙ ২ + রৈখিক_সূচক((০,১), (২,২))
= (১ ∙ ৩ + ১) ∙ ২ ∙ ২ + (০ ∙ ২ + ১)
= ১৭।
\[ LinearIndexWithTile((2,3), (3,5), (2,2)) \\ = LinearIndex((1,1,0,1), (2,3,2,2)) \\ = LinearIndex((1,1), (2,3)) \cdot 2 \cdot 2 + LinearIndex((0,1), (2,2)) \\ = (1 \cdot 3 + 1) \cdot 2 \cdot 2 + (0 \cdot 2 + 1) \\ = 17 \]
প্যাড-রিশেপ-ট্রান্সপোজ হিসাবে টাইলিং
টাইলিং-ভিত্তিক লেআউট নিম্নরূপ কাজ করে:
মাত্রার একটি অ্যারে বিবেচনা করুন (d n , d n-1 , ..., d1) (d1 হল সবচেয়ে গৌণ মাত্রা)। যখন এটি আকারের টাইলিং (t n , t n-1 , ..., t 1 ) (t 1 হল সবচেয়ে গৌণ মাত্রা) দিয়ে সাজানো হয়, তখন সেই টাইলিংকে প্যাড-রিশেপ-ট্রান্সপোজের পরিপ্রেক্ষিতে নিম্নলিখিত উপায়ে বর্ণনা করা যেতে পারে।
- অ্যারেটি (⌈d n /t n ⌉∙t n , ... , ⌈d 1 /t 1 ⌉∙t 1 ) এ প্যাড করা হয়েছে।
- প্রতিটি মাত্রা i কে (⌈d i /t i ⌉, t i ) এ বিভক্ত করা হয়েছে, অর্থাৎ অ্যারেটিকে পুনরায় আকার দেওয়া হয়েছে
(⌈d n /t n ⌉, t n , ... , ⌈d 1 /t 1 ⌉, t 1 )।
এই রিশেপে নিজে থেকে কোনও ভৌত বিন্যাস পরিবর্তন হয় না, তাই এই রিশেপটি একটি বিটকাস্ট। যদি কেউ স্পষ্টভাবে টাইলিং সম্পর্কে চিন্তা না করে থাকেন, তাহলে এই রিশেপটি প্যাডেড আকৃতির মতো একই সংখ্যক উপাদান সহ যেকোনো আকৃতি প্রকাশ করতে পারে - এখানে উদাহরণটি হল কীভাবে একটি টাইলকে এইভাবে প্রকাশ করা যায়। - একটি স্থানান্তর ঘটে যখন t n , ..., t 1 কে সবচেয়ে গৌণ মাত্রায় স্থানান্তরিত করা হয় এবং তাদের আপেক্ষিক ক্রম বজায় রাখা হয়, যাতে সর্বাধিক বৃহৎ থেকে সর্বাধিক গৌণ মাত্রার ক্রম হয়
(⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉, t n , ... , t 1 )।
চূড়ান্ত আকৃতিতে উপসর্গ আছে
(⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉), যা প্রতিটি মাত্রায় টাইলের সংখ্যা বর্ণনা করে। অ্যারের একটি উপাদান (e n , ... , e 1 ) চূড়ান্ত আকারে এই উপাদানের সাথে ম্যাপ করা হয়:
(⌊e n /t n ⌋, ... , ⌊e 0 /t 0 ⌋, e n mod t n , ... , e 1 mod t 1 )। এটা সহজেই দেখা যায় যে উপাদানটির রৈখিক সূচক উপরের সূত্রটি প্রত্যাশিতভাবে অনুসরণ করে।
বারবার টাইলিং
XLA এর টাইলিং বারবার প্রয়োগ করলে এটি আরও নমনীয় হয়ে ওঠে।
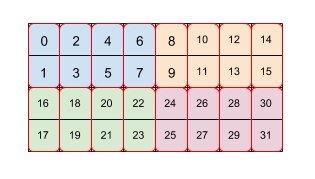
চিত্র ২
চিত্র ২ দেখায় কিভাবে ৪x৮ আকারের একটি অ্যারে দুটি স্তরের টাইলিং (প্রথম ২x৪ তারপর ২x১) দ্বারা টাইল করা হয়। আমরা এই পুনরাবৃত্ত টাইলিংকে (২,৪)(২,১) হিসাবে উপস্থাপন করি। প্রতিটি রঙ একটি ২x৪ টাইল নির্দেশ করে এবং প্রতিটি লাল বর্ডার বাক্স একটি ২x১ টাইল। সংখ্যাগুলি টাইলযুক্ত বিন্যাসে সেই উপাদানের স্মৃতিতে রৈখিক সূচক নির্দেশ করে। এই বিন্যাসটি TPU-তে BF16-এর জন্য ব্যবহৃত বিন্যাসের সাথে মেলে, তবে প্রাথমিক টাইলটি বড়, অর্থাৎ টাইলিংটি (8,128)(2,1), যেখানে ২x১ দ্বারা দ্বিতীয় টাইলিং এর উদ্দেশ্য হল দুটি ১৬-বিট মান একত্রিত করে একটি ৩২-বিট মান তৈরি করা যা একটি TPU এর স্থাপত্যের সাথে সামঞ্জস্যপূর্ণ।
মনে রাখবেন যে একটি দ্বিতীয় বা পরবর্তী টাইল উভয় মাইনর-ইন-টাইল ডাইমেনশনকেই নির্দেশ করতে পারে, যা কেবল টাইলের মধ্যে ডেটা পুনর্বিন্যাস করে, যেমনটি এই উদাহরণে (8,128)(2,1) এর ক্ষেত্রে দেখা গেছে, তবে এটি পূর্ববর্তী টাইলিং থেকে প্রধান ক্রস-টাইল ডাইমেনশনকেও নির্দেশ করতে পারে।
টাইলস ব্যবহার করে মাত্রা একত্রিত করা
XLA-এর টাইলিং মাত্রা একত্রিত করাকেও সমর্থন করে। উদাহরণস্বরূপ, এটি F32[2,7,8,11,10]{4,3,2,1,0}-এর মাত্রাগুলিকে F32[112,110]{1,0}-এর সাথে একত্রিত করতে পারে এবং প্রথমে (2,3) দিয়ে টাইলিং করতে পারে। ব্যবহৃত টাইলটি হল (∗,∗,2,∗,3)। এখানে একটি টাইলের একটি তারকাচিহ্ন বোঝায় যে সেই মাত্রাটি নেওয়া এবং পরবর্তী আরও গৌণ মাত্রার সাথে এটিকে একত্রিত করা। একাধিক সংলগ্ন মাত্রা একসাথে একটি মাত্রায় অন্তর্ভুক্ত করা যেতে পারে। একটি সাবসামড ডাইমেনশন টাইলের সেই মাত্রায় -1 এর একটি টাইলের মান দ্বারা প্রতিনিধিত্ব করা হয়, যা অন্যথায় একটি টাইলে মাত্রা আকার হিসাবে বৈধ নয়।
আরও স্পষ্ট করে বলতে গেলে, যদি টাইলের একটি তারকাচিহ্নের মাধ্যমে আকৃতির মাত্রা i বাদ দেওয়া হয়, তাহলে টাইলিং এর পূর্ববর্তী সংজ্ঞা প্রয়োগ করার আগে, টাইল করা আকৃতি এবং টাইল ভেক্টর উভয় থেকে সেই মাত্রাটি সরিয়ে ফেলা হয়, এবং আকৃতির মাত্রা i-1 এর অ্যারে বাউন্ড d i-1 থেকে d i d i-1 পর্যন্ত বৃদ্ধি করা হয়। টাইল ভেক্টরের প্রতিটি তারকাচিহ্নের জন্য এই ধাপটি পুনরাবৃত্তি করা হয়।
টাইলিং ফর্ম্যাটের উদাহরণ
এই বিভাগে জনপ্রিয় XLA ফর্ম্যাটের উদাহরণ দেখানো হয়েছে।
- আনলিটেড ফর্ম্যাট - TPU তে না থাকা বেশিরভাগ অ্যারে একটি আনলিটেড রৈখিক ফর্ম্যাট ব্যবহার করে, যেমন C++।
- TPU টাইল ফর্ম্যাট - XLA/TPU তে সবচেয়ে সাধারণ ফর্ম্যাট হল
8x128দ্বারা টাইলিং, যা একটি TPU তে 32-বিট8x128ভেক্টর রেজিস্টারের সাথে মেলে। - TPU ছোট টাইল ফর্ম্যাট (যা "কম্প্যাক্ট ২য় মাইনর লেআউট" নামেও পরিচিত) - যখন দ্বিতীয় সবচেয়ে ছোট মাত্রার আকার ১ বা ২ হয়, তখন XLA/TPU এর পরিবর্তে
2x128টাইল ব্যবহার করে মেমরি বাঁচান কারণ2x128টাইল8x128টাইল থেকে ছোট। যখন দ্বিতীয় সবচেয়ে ছোট মাত্রার আকার 3 বা 4 হয়, তখন XLA/TPU টাইল4x128টাইল ব্যবহার করে। - TPU 16 বিট টাইল ফর্ম্যাট - যখন অ্যারে এলিমেন্ট টাইপ BF16 হয়, তখন আমরা সাধারণত (8,128)(2,1) ব্যবহার করি। দ্বিতীয় স্তরের টাইলিং তথাকথিত BF16 প্যাকিং করে। উপরের চিত্র 2 দেখুন, একটি জোড় সারি থেকে একটি উপাদান এবং একটি বিজোড় সারি থেকে একটি উপাদান একসাথে সাজানো হয়েছে এবং একটি 32-বিট এলিমেন্টে রাখা হয়েছে। এই ফর্ম্যাটটি ব্যবহার করা হয় কারণ TPU গুলি 32 বিট মান নিয়ে কাজ করে এবং সবচেয়ে ছোট মাত্রার তুলনায় দ্বিতীয় সবচেয়ে ছোট মাত্রা জুড়ে ডেটা স্থানান্তর করা অনেক বেশি দক্ষ, তাই একই কলাম থেকে 32 বিট পেতে দুটি 16 বিট মান সংগ্রহ করা একই সারি থেকে দুটি 16 বিট মান নেওয়ার চেয়ে অনেক বেশি কার্যকর।
- TPU 8 বিট টাইল ফর্ম্যাট - এখানে ফর্ম্যাটটি 16 বিট ফর্ম্যাটের সাথে খুব মিল, পার্থক্য হল আমাদের 32 বিট পেতে কেবল দুটির পরিবর্তে 4 টি উপাদান একত্রিত করতে হবে, তাই টাইলিংটি হয়ে যায়
(8,128)(4,1)। - TPU ১ বিট টাইল ফর্ম্যাট - TPU গুলি বর্তমানে একটি বুলিয়ান মানের জন্য ১ বাইট ব্যবহার করে, অর্থাৎ PRED এলিমেন্ট টাইপের বাইটে আকার ১।
(32,128)(32,1)দ্বারা টাইলিং ব্যবহার করা এবং প্রতি এলিমেন্টে মাত্র ১ বিট ব্যবহার করা কম অপচয় হবে।

