XLA TPU использует различные форматы на основе плиток из-за двумерной природы своих векторных регистров.
Плиточные форматы
Плиточный формат разбивает фигуру на плитки (обычно одномерные или двумерные). Плитки располагаются в памяти в порядке от старшего к младшему (построчная компоновка). Элементы внутри плитки также располагаются в порядке от старшего к младшему.
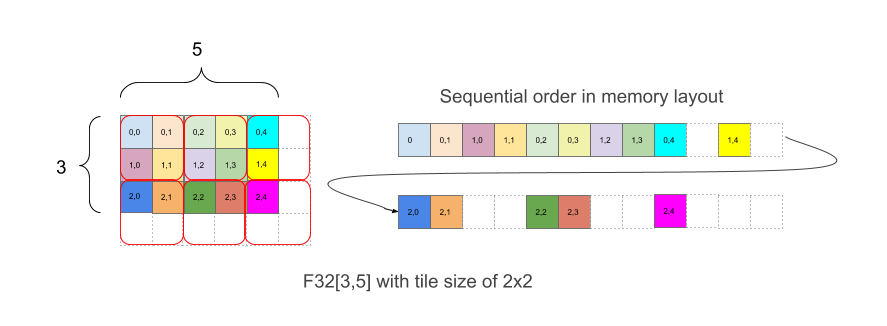
Рисунок 1
На рисунке 1 показано, как массив F32[3,5] размещён в памяти плиткой 2x2. Форма с такой разметкой записывается как F32[3,5]{1,0:T(2,2)}, где 1,0 относится к физическому порядку измерений (поле minor_to_major в Layout), а (2,2) после двоеточия указывает на разбиение физических измерений плиткой 2x2.
Интуитивно понятно, что плитки выкладываются так, чтобы покрыть фигуру, а затем внутри каждой плитки элементы выкладываются без заполнения, как в примере выше, где правая часть примера показывает макет в памяти, включая белые элементы заполнения, которые добавляются для того, чтобы получить полные плитки 2x2, даже если исходные границы массива неровные.
Дополнительные элементы в заполнении не обязательно должны содержать какое-либо конкретное значение.
Формулы линейного индекса для замощения по заданной форме и плитке
Без разбиения на блоки элемент e=( en , e n-1 , ..., e 1 ) в массиве с границами массива d=(d n , d n-1 , ..., d 1 ) (d1 — наименьшее измерение) размещается в порядке от большего к меньшему в позиции:
линейный_индекс(e, d)
= linear_index(( en , en-1 , ..., e1 ), ( dn , dn-1 , ..., d1 ))
= енд н-1 ...д 1 + ен -1 д н -2 ...д 1 + ... + е 1
Для простоты обозначений в этом документе мы предполагаем, что плитка имеет то же количество измерений, что и массив. В реализации тайлинга в XLA это обобщено для тайлингов с меньшим количеством измерений: начальные самые большие измерения остаются неизменными, а тайлинг применяется только к самым малым измерениям, так что указанный тайлинг содержит суффикс физических измерений разбиваемой фигуры.
При использовании мозаики размером (t n , t n-1 , ... , t 1 ) элемент в массиве с индексами (e n , e n-1 , ... , e 1 ) сопоставляется с этой позицией в окончательном макете:
linear_index_with_tile(e, d, t)
= linear_index((⌊e/t⌋, e mod t), (⌈d/t⌉, t)) (арифметика поэлементная, (a,b) — конкатенация)
= linear_index((⌊e n /t n ⌋, ... , ⌊e 1 /t 1 ⌋, e n mod t n , ... , e 1 mod t 1 ), (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉, t n , t n-1 , ... , t 1 ))
= линейный_индекс((⌊e n /t n ⌋, ... , ⌊e 1 /t 1 ⌋), (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉))∙t n t n-1 ...t 1 + линейный_индекс(( en mod t n , ... , e 1 mod t 1 ), (t n , t n-1 , ... , t 1 ))
Макет можно представить как состоящий из двух частей: (⌊e n /t n ⌋, ... , ⌊e 1 /t 1 ⌋), что соответствует индексу плитки в массиве плиток размером (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉), и ( en mod t n , ... , e 1 mod t 1 ), что соответствует индексу внутри плитки. Функция ceil появляется в ⌈d i /t i ⌉, потому что если плитки выходят за границы большего массива, вставляется отступ, как показано на рисунке 1. Как плитки, так и элементы внутри плиток выкладываются рекурсивно без заполнения.
В примере на рисунке 1 элемент (2,3) имеет индекс тайла (1,1) и индекс внутри тайла (0,1) для объединённого вектора координат (1,1,0,1). Индексы тайлов имеют границы (2,3), а сам тайл имеет границу (2,2) для объединённого вектора (2,3,2,2). Линейный индекс с тайлом для элемента с индексом (2,3) в логической форме равен
linear_index_with_tile((2,3), (3,5), (2,2))
= линейный_индекс((1,1,0,1), (2,3,2,2))
= линейный_индекс((1,1), (2,3)) ∙ 2 ∙ 2 + линейный_индекс((0,1), (2,2))
= (1 ∙ 3 + 1) ∙ 2 ∙ 2 + (0 ∙ 2 + 1)
= 17.
\[ LinearIndexWithTile((2,3), (3,5), (2,2)) \\ = LinearIndex((1,1,0,1), (2,3,2,2)) \\ = LinearIndex((1,1), (2,3)) \cdot 2 \cdot 2 + LinearIndex((0,1), (2,2)) \\ = (1 \cdot 3 + 1) \cdot 2 \cdot 2 + (0 \cdot 2 + 1) \\ = 17 \]
Тайлинг как pad-reshape-transpose
Макет на основе тайлинга работает следующим образом:
Рассмотрим массив размерностей (d n , d n-1 , ... , d1) (d1 — наименьшая размерность). Разбитый на плитки размером (t n , t n-1 , ... , t 1 ) (t 1 — наименьшая размерность), этот массив можно описать в терминах pad-reshape-transpose следующим образом.
- Массив дополняется до (⌈d n /t n ⌉∙t n , ... , ⌈d 1 /t 1 ⌉∙t 1 ).
- Каждое измерение i разбивается на (⌈d i /t i ⌉, t i ), т.е. массив преобразуется в
(⌈d n /t n ⌉, t n , ... , ⌈d 1 /t 1 ⌉, t 1 ).
В этом преобразовании нет никаких физических изменений в макете, поэтому оно представляет собой биткаст. Если речь не идёт о тайлинге, то это преобразование может представлять любую фигуру с тем же количеством элементов, что и у формы с отступами. Приведённый здесь пример показывает, как представить тайл таким образом. - Транспонирование происходит путем перемещения t n , ... , t 1 к самым младшим измерениям с сохранением их относительного порядка, так что порядок измерений от самых больших к самым младшим становится
(⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉, t n , ... , t 1 ).
Окончательная форма имеет префикс
(⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉), что описывает количество плиток в каждом измерении. Элемент массива ( en , ... , e 1 ) сопоставляется этому элементу в итоговой форме:
(⌊e n /t n ⌋, ... , ⌊e 0 /t 0 ⌋, en mod t n , ... , e 1 mod t 1 ). Легко видеть, что линейный индекс элемента следует формуле выше, как и ожидалось.
Повторяющаяся укладка плитки
Мозаика XLA становится еще более гибкой, если применять ее повторно.
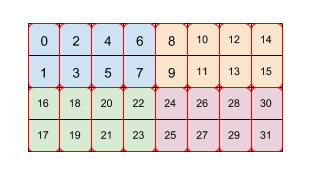
Рисунок 2
На рисунке 2 показано, как массив размером 4x8 разбивается на два уровня (сначала 2x4, затем 2x1). Мы представляем эту повторяющуюся разбивку как (2,4)(2,1). Каждый цвет обозначает плитку 2x4, а каждый красный рамочный блок — плитку 2x1. Числа указывают линейный индекс в памяти этого элемента в формате разбивки. Этот формат совпадает с форматом, используемым для BF16 на TPU, за исключением того, что начальная плитка больше, а именно разбивка имеет вид (8,128)(2,1), где цель второй разбивки на плитки 2x1 — объединить два 16-битных значения в одно 32-битное значение способом, соответствующим архитектуре TPU.
Обратите внимание, что вторая или последующая плитка может ссылаться как на второстепенные измерения внутри плитки, которые просто переупорядочивают данные внутри плитки, как в этом примере с (8,128)(2,1), так и на основные межплиточные измерения из предыдущей плитки.
Объединение размеров с помощью плиток
Тайлы XLA также поддерживают комбинирование измерений. Например, измерения из F32[2,7,8,11,10]{4,3,2,1,0} можно объединить в F32[112,110]{1,0}, а затем наложить на него тайл (2,3). Используемый тайл — (∗,∗,2,∗,3). Звездочка в тайле означает, что это измерение объединяется со следующим, более мелким, измерением. Несколько смежных измерений могут быть объединены в одно измерение. Объединенное измерение представлено значением тайла -1 в этом измерении тайла, что в противном случае недопустимо в тайле как размер измерения.
Точнее, если измерение i фигуры исключается с помощью звёздочки в плитке, то перед применением предыдущего определения тайлинга это измерение удаляется как из тайловой фигуры, так и из вектора тайла, а измерение i-1 фигуры увеличивает свою границу массива с d i-1 до d i d i-1 . Этот шаг повторяется для каждой звёздочки в векторе тайла.
Примеры форматов тайлинга
В этом разделе представлены примеры популярных форматов XLA.
- Необработанный формат . Большинство массивов, отсутствующих в TPU, используют необработанный линейный формат, такой же, как, например, в C++.
- Формат плитки TPU . Наиболее распространенным форматом в XLA/TPU является плитка размером
8x128, что соответствует 32-битным векторным регистрам8x128на TPU. - Формат плиток TPU Small (также известный как «Компактная 2-я второстепенная раскладка») — если второй по величине размер равен 1 или 2, XLA/TPU использует плитки размером
2x128для экономии памяти, поскольку плитка2x128меньше, чем плитка8x128. Если второй по величине размер равен 3 или 4, XLA/TPU использует плитки размером4x128. - Формат тайлов TPU 16 бит — если тип элемента массива — BF16, мы обычно используем тайлы (8,128)(2,1). Второй уровень тайлинга реализует так называемую упаковку BF16. См. рисунок 2 выше, один элемент из чётной строки и один элемент из нечётной строки размещаются вместе и помещаются в один 32-битный элемент. Этот формат используется, поскольку TPU изначально работают с 32-битными значениями, и гораздо эффективнее перемещать данные по второму младшему измерению, чем по самому младшему. Поэтому сбор двух 16-битных значений для получения 32 бит из одного столбца гораздо эффективнее, чем более очевидным способом — извлечение двух 16-битных значений из одной строки.
- Формат плитки TPU 8 бит - этот формат очень похож на 16 бит, разница лишь в том, что нам нужно собрать вместе 4 элемента, чтобы получить 32 бита, а не только два, поэтому плитка становится
(8,128)(4,1). - 1-битный формат тайла TPU — в настоящее время TPU используют 1 байт для одного логического значения, т.е. размер в байтах типа элемента PRED равен 1. Менее расточительным было бы использовать тайл по
(32,128)(32,1)и использовать только 1 бит на элемент.

