รูปที่ 1
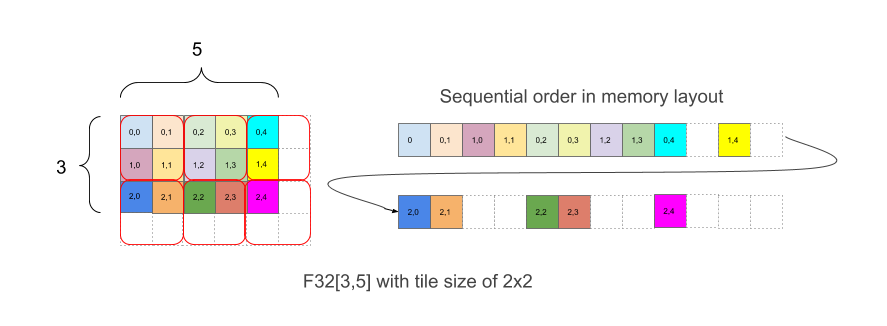
รูปที่ 1 แสดงการจัดเรียงอาร์เรย์ F32[3,5] ในหน่วยความจำที่มีการเรียงชิดกันขนาด 2x2 รูปร่างที่มีเลย์เอาต์นี้จะเขียนเป็น F32[3,5]{1,0:T(2,2)} โดยที่ 1,0 เกี่ยวข้องกับ
ลำดับทางกายภาพของขนาด (ช่อง minor_to_major ในเลย์เอาต์) ขณะที่ (2,2)
หลังจากเครื่องหมายโคลอนหมายถึงการเรียงต่อกันของขนาดจริงด้วยไทล์ 2x2
โดยปกติจะมีการวางชิ้นส่วนไว้เพื่อบดบังรูปร่าง จากนั้นภายในแต่ละไทล์จะมีการวางองค์ประกอบโดยไม่มีการเรียงต่อกันเหมือนในตัวอย่างด้านบนโดยที่ส่วนขวาของตัวอย่างแสดงเลย์เอาต์ในหน่วยความจำ ซึ่งรวมถึงองค์ประกอบระยะห่างจากขอบสีขาวที่เพิ่มเข้ามาเพื่อให้ชิ้นส่วนขนาด 2x2 สมบูรณ์ แม้ว่าขอบเขตของอาร์เรย์เดิมจะไม่เท่ากันก็ตาม
คุณไม่จำเป็นต้องใส่ค่าเฉพาะใดๆ ในองค์ประกอบเพิ่มเติมในระยะห่างจากขอบ
สูตรดัชนีเชิงเส้นสำหรับการเรียงต่อกันของรูปร่างและชิ้นส่วน
หากไม่มีการเรียงต่อกัน องค์ประกอบ e=(en, en-1, ... , e1) ในอาร์เรย์ที่มีขอบเขตของอาร์เรย์ d=(dn, dn-1, ... , d1) (d1 คือมิติข้อมูลรองลงมา) จะมีการจัดรูปแบบตามอันดับย่อยที่สุดในตำแหน่งต่อไปนี้
linear_index(e, d)
= เชิงเส้นดัชนี((en, en-1, ... , e1),
(dn, dn-1, ... , d1))
= endn-1...d1 +n-1...1 +n-1 ...n-1)
= en dn-1...d1 +n-1 n-1
เพื่อให้อ่านง่ายขึ้นในเอกสารนี้ เราถือว่าชิ้นส่วนมีจำนวนมิติข้อมูลเท่ากับอาร์เรย์ ในการใช้งานการเรียงต่อของ XLA โดยทั่วไปแล้วจะหมายถึงการไทล์ที่มีขนาดน้อยกว่าโดยปล่อยให้ขนาดส่วนใหญ่เริ่มต้นไว้ตามเดิม และนำไปใช้กับขนาดที่มีขนาดเล็กที่สุดเท่านั้น เพื่อให้ไทล์ที่ระบุกล่าวถึงส่วนต่อท้ายของขนาดรูปร่างที่แบ่งชิ้นส่วน
เมื่อใช้การเรียงตัวของขนาด (tn, tn-1, ... , t1) องค์ประกอบในอาร์เรย์ที่มีดัชนี (en, en-1, ... , e1) จะจับคู่ที่ตำแหน่งนี้ในเลย์เอาต์สุดท้าย
⋌1,nn(1)n,n,n
ซึ่งเลย์เอาต์จะมี 2 ส่วน ดังนี้ (⌊en/tn⌋, ... , ⌊e1/t1⌋) ซึ่งสอดคล้องกับดัชนีไทล์ในอาร์เรย์ของชิ้นส่วนขนาด (⌈dn/tn⌉, ....1, ฟังก์ชัน Ceil จะปรากฏใน ⌈di/ti⌉ เนื่องจากหากไทล์ทับขอบเขตของอาร์เรย์ที่ใหญ่กว่า ระบบจะแทรกระยะห่างจากขอบดังที่แสดงในรูปที่ 1 ทั้งชิ้นส่วนและองค์ประกอบภายในชิ้นส่วน จะจัดวางซ้ำโดยไม่มีการเรียงต่อกัน
สำหรับตัวอย่างในรูปที่ 1 องค์ประกอบ (2,3) มีดัชนีไทล์ (1,1) และดัชนีภายในไทล์ (0,1) สำหรับเวกเตอร์พิกัดแบบรวมเป็น (1,1,0,1) ดัชนีไทล์มีขอบเขต (2,3) และตัวไทล์เองคือ (2,2) สำหรับเวกเตอร์รวมกันของ (2,3,2,2) จากนั้นดัชนีเชิงเส้นที่มีไทล์สำหรับองค์ประกอบที่มีดัชนี (2,3) ในรูปร่างเชิงตรรกะ
เชิงเส้น_ดัชนี_ไทล์((2,3), (3,5), (2,2))
= เชิงเส้น_ดัชนี((1,1,0,1), (2,3,2,2))
= เชิงเส้น_ดัชนี(2,2))
= เชิงเส้น_ดัชนี((1,1,0,1), (2,3,2,2))
= เชิงเส้น_ดัชนี((1,1), (2,3)) × (2,3))
การเรียงต่อกันแบบการเปลี่ยนรูปร่างแผ่น
เลย์เอาต์แบบต่อไทล์มีการทำงานดังนี้
พิจารณาอาร์เรย์ของมิติข้อมูล (dn, dn-1, ... , d1) (d1 เป็นมิติข้อมูลน้อยที่สุด) เมื่อวางชิ้นส่วนขนาด (tn, tn-1, ... , t1) (t1 คือขนาดย่อยที่สุด) การเรียงต่อกันสามารถอธิบายในรูปของการสับเปลี่ยนรูปร่างแผ่นได้ดังต่อไปนี้
- ระบบจะเพิ่มอาร์เรย์เป็น (⌈dn/tn⌉ จึงทำให้n, ... , ⌈d1/t1⌉ t1)
- มิติข้อมูลแต่ละรายการ i จะแบ่งเป็น (⌈di/ti⌉,
ti) นั่นคือ อาร์เรย์ปรับรูปเป็น
(⌈dn/tn⌉, tn, ... , ⌈d1/t1⌉, t1)
ไม่มีการเปลี่ยนแปลงเลย์เอาต์ทางกายภาพในการปรับรูปร่างนี้ การปรับรูปร่างนี้จึงเป็นการใส่บิตแคสต์ หากไม่ได้นึกถึงการเรียงต่อกันอย่างชัดเจน การปรับรูปร่างนี้สามารถแสดงรูปร่างใดก็ได้ที่มีจำนวนองค์ประกอบเท่ากับรูปร่างที่มีการเสริมกัน ตัวอย่างนี้คือวิธีแสดงชิ้นส่วนในลักษณะนี้ - การสลับฉากจะเกิดขึ้นโดยเลื่อนn, ... , t1 ไปยังมิติข้อมูลย่อยที่สุดขณะรักษาลำดับที่เกี่ยวข้องไว้ เพื่อให้ลำดับของมิติข้อมูลจากสำคัญที่สุดไปจนถึงย่อยส่วนใหญ่กลายเป็น
(⌈dn/tn⌉, ... , ⌈d1/t1,n,
รูปร่างสุดท้ายจะมีคํานําหน้า
(⌈dn/tn⌉, ... ,
⌈d1/t1⌉) ซึ่งอธิบายจํานวนชิ้นส่วนในแต่ละ
มิติข้อมูล องค์ประกอบในอาร์เรย์ (en, ... , e1) ได้รับการจับคู่กับองค์ประกอบนี้ในรูปร่างสุดท้ายแล้ว:
(⌊en/tn⌋, ... ,
⌊e0/t0⌋, en mod tn, ... ,
e1 สังเกตได้ง่ายๆ ว่าดัชนีเชิงเส้นขององค์ประกอบเป็นไปตามสูตรด้านบนตามที่คาดไว้
การปูกระเบื้องซ้ำ
การปูกระเบื้องของ XLA จะยืดหยุ่นมากขึ้นเมื่อนำมาใช้ซ้ำๆ
รูปที่ 2
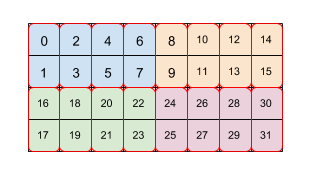
รูปที่ 2 แสดงการเรียงไทล์ขนาด 4x8 ของอาร์เรย์ 2 ระดับ (2x4 แรกตามด้วย 2x1) เราแสดงการเรียงต่อกันซ้ำนี้เป็น (2,4)(2,1) แต่ละสีหมายถึงไทล์ขนาด 2x4 และขอบสีแดงแต่ละกล่องคือชิ้นส่วนขนาด 2x1 ตัวเลขจะระบุดัชนีเชิงเส้นในหน่วยความจำขององค์ประกอบดังกล่าวในรูปแบบไทล์ รูปแบบนี้ตรงกับรูปแบบที่ใช้สำหรับ BF16 บน TPU เว้นแต่ว่าไทล์เริ่มต้นที่ใหญ่กว่า กล่าวคือไทล์ที่ 2 คือ (8,128)(2,1) โดยที่วัตถุประสงค์ของไทล์ที่ 2 คูณ 2x1 คือการรวบรวมค่า 16 บิต 2 ค่าเข้าด้วยกันเพื่อสร้างค่า 32 บิต 1 รายการที่สอดคล้องกับสถาปัตยกรรมของ TPU
โปรดทราบว่าการ์ดที่ 2 หรือไทล์ที่ 2 อาจหมายถึงทั้งมิติข้อมูลภายในไทล์ย่อย ซึ่งเพียงแค่จัดเรียงข้อมูลใหม่ภายในไทล์ ตามที่แสดงในตัวอย่างนี้คือ (8,128)(2,1) แต่ก็อ้างอิงถึงมิติข้อมูลแบบครอสไทล์หลักจากการเรียงต่อกันก่อนหน้าได้เช่นกัน
การรวมมิติข้อมูลโดยใช้ชิ้นส่วนข้อมูล
การแยกไทล์ของ XLA ยังรองรับการรวมมิติข้อมูลด้วย เช่น อาจรวมมิติข้อมูลใน F32[2,7,8,11,10]{4,3,2,1,0} เป็น F32[112,110]{1,0} ก่อนนำไปต่อกับ (2,3) ไทล์ที่ใช้คือ (Congratulations, \r,2,ใช้ไม่ได้,3) นี่เป็นเครื่องหมายดอกจันในไทล์ที่บ่งบอกว่ามีการใช้มิติข้อมูลนั้นและนำไปรวมกับมิติข้อมูลที่รองลงมา มิติข้อมูลที่อยู่ติดกันหลายรายการสามารถรวมอยู่ในมิติข้อมูลเดียว มิติข้อมูลย่อยจะแสดงด้วยค่าไทล์เป็น -1 ในมิติข้อมูลดังกล่าวของชิ้นส่วนดังกล่าว ซึ่งไม่มีในไทล์ที่เป็นขนาดมิติข้อมูล
กล่าวคือ หากมิติข้อมูล i ของรูปร่างถูกตัดออกผ่านเครื่องหมายดอกจันในชิ้นส่วน ก่อนที่จะมีการใช้คำจำกัดความก่อนหน้าของการเรียงต่อ มิติข้อมูลดังกล่าวจะถูกลบออกจากทั้งรูปร่างที่แบ่งชิ้นส่วนและเวกเตอร์ของชิ้นส่วน และมิติข้อมูล i-1 ของรูปร่างมีขอบเขตอาร์เรย์เพิ่มขึ้นจาก di-1 เป็น didi-1 ขั้นตอนนี้จะเล่นซ้ำสำหรับเครื่องหมายดอกจันแต่ละเครื่องหมายใน เวกเตอร์ของไทล์
