平铺布局

图 1

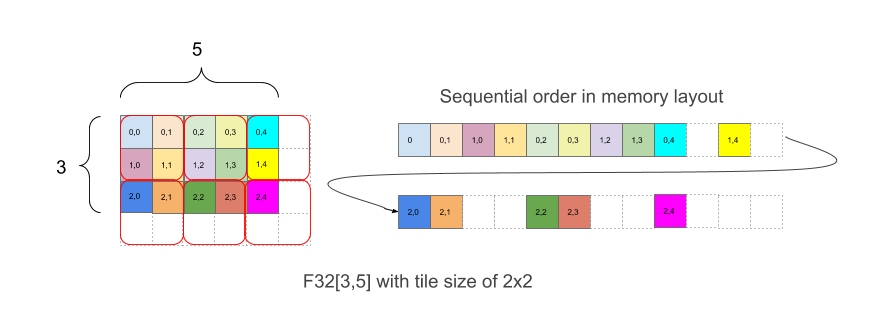
图 1 显示了如何使用 2x2 平铺在内存中布局 F32[3,5] 数组。采用此布局的形状编写为 F32[3,5]{1,0:T(2,2)}，其中 1,0 代表尺寸的物理顺序（布局中的 minor_to_major 字段），而冒号后面的 (2,2) 表示以 2x2 图块平铺物理尺寸。

直观地说，平铺的布局是覆盖形状，然后在每个图块中，元素在布局时不会平铺，如上例所示。在上例中，示例的右侧部分显示了内存中的布局，包括为了拥有完整的 2x2 图块而添加的白色内边距元素，尽管原始数组边界并不均匀。

内边距中的额外元素无需包含任何特定值。

给定形状和图块的平铺线性索引公式

在没有平铺的情况下，数组边界为 d=(d_n, d_n-1, ... , d₁) 的数组中的元素 e=(e_n, e_n-1, ... , e₁)（d1 是最次要的维度）在以下位置按主要顺序排列：

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ +_n-1 +_...dn-2

为简单起见，在本文档中，我们假设功能块与数组具有相同的维度数。在 XLA 的平铺实现中，这泛用于维度较少的平铺，具体做法是保持初始最主要维度不变，并仅将平铺应用于最小尺寸，这样指定的平铺操作会提及正在平铺的形状的物理尺寸后缀。

使用大小为 t_n、t_n-1、...、t₁ 的平铺图片时，数组中具有索引（e_n、e_n-1、...、e₁）的元素会映射到最终布局中的此位置：

n_index_with_tile(e, d1 / mod 1 ) <sub>n


n</sub>

该布局可以视为由两部分组成：(🚌?e_n/t_n🎈?, ... , Increasee₁/t₁ಠ)，它对应一个大小为 (allocated_n/t_n↩, ..., gclsrcd₁/t₁之间的差异) 和 mod (e ..._n mod ..._n) 中的图块索引。ceil 函数出现在;">d_i/t_iDATASET 中，因为如果图块超出较大数组的边界，系统会插入填充，如图 1 所示。功能块中的图块和元素均以递归方式进行布局，而不是平铺。

对于图 1 中的示例，对于 (1,1,0,1) 的组合坐标矢量，元素 (2,3) 具有图块索引 (1,1) 和图块内索引 (0,1)。对于 (2,3,2,2) 的组合矢量，图块索引具有边界 (2,3)，而图块本身为 (2,2)。然后，逻辑形状中具有索引 (2,3) 的元素平铺的线性索引为

平铺为衬垫重塑转置

基于平铺的布局的运作方式如下：
假设有一个维度数组（d_n、d_n-1、...、d1），d1 是最小的维度。当以大小（t_n、t_n-1、...、t₁）（t₁ 是最次要维度）进行布局时，可以通过以下方式根据“pad-reshape-transpose”（填充变形转置）对平铺进行描述。

1. 该数组已填充到 (d_n/t_n↩•t_n, ... () , appropriated₁/t₁与您联系 t₁)。
2. 每个维度 i 被拆分为“深度”/ti“t”，即“t_i”数组，即数组被重新调整为“
   ”（“NUMBEROFd_n/t_n↩, t_n, ..., }{/d₁/t₁↩, t₁”）。
   此重塑本身并没有物理布局更改，因此此重塑属于 bitcast。如果未明确想到图块，这种重塑可以表达与填充形状具有相同数量元素的任何形状 - 此处的示例展示了如何以这种方式表示图块。
3. 将 t_n、...、t₁ 移到最次要维度，同时保持其相对顺序，这样就会发生转置。因此，维度从最主要维度到最小维度的顺序变为
   （过去 t_n/t_n甚至可以...、要修改的 t₁/t₁提高、t_n、...、t₁）。

最终形状的前缀为
(🙌?d_n/t_n联邦, ... , appropriated₁/t₁')}>，表示每个维度的图块数量。数组中的某个元素（e_n、...、e₁）以最终形状映射到此元素：
( News e_n/t_n🛈?, ... , ₽₀/t₀扩展, e_n mod t_n, ... , e₁ mod t₁)。很容易看出，元素的线性索引符合上述公式预期。

重复平铺

通过反复应用，XLA 的平铺图片变得更加灵活。

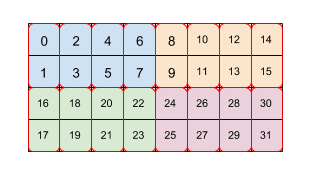
图 2

图 2 显示了如何将大小为 4x8 的数组按两个平铺级别（先是 2x4，然后是 2x1）平铺。我们将这种重复的平铺表示为 (2,4)(2,1)。每种颜色表示一个 2x4 图块，每个红色边框框都是一个 2x1 图块。数字表示平铺格式该元素在内存中的线性索引。此格式与 TPU 上用于 BF16 的格式相符，不同之处在于初始图块较大，即平铺为 (8,128)(2,1)，其中通过 2x1 平铺的第二个平铺的目的是将两个 16 位值汇集在一起，形成一个 32 位值，以便与 TPU 的架构保持一致。

请注意，第二个或更晚的图块可以指代图块内的次要维度，这仅会重新排列图块内的数据（如本例中为 (8,128)(2,1)），但也可以引用之前图块的主要跨图块维度。

使用图块合并尺寸

XLA 的平铺功能还支持组合维度。例如，它可以先将 F32[2,7,8,11,10]{4,3,2,1,0} 中的维度合并到 F32[112,110]{1,0}，然后再将其与 (2,3) 平铺。使用的图块为 (†,\{,2,\{,3)。在这里，功能块中的星号表示采用该维度并将其与下一个次要维度结合起来。多个相邻的维度可组合为一个维度。子维度由图块维度中图块值为 -1 的图块值表示，而该维度在图块中作为尺寸大小无效。

更确切地说，如果通过图块中的星号消除形状的维度 i，那么在应用平铺的先前定义之前，系统会从正在平铺的形状和图块矢量中移除该维度，并且形状的维度 i-1 的数组边界从 d_i-1 增加到 d_id_i-1。系统会对图块矢量中的每个星号重复此步骤。