الانتشار

نظرة عامة

يستخدم انتشار التجزئة عمليات التجزئة التي يحدّدها المستخدم لاستنتاج عمليات التجزئة غير المحدّدة للمصفوفات (أو سمة محدّدة من المصفوفات). وينتقل من خلال تدفق البيانات (سلاسل الاستخدام والتعريف) لرسم البياني الحسابي في كلا الاتجاهين إلى أن يتم الوصول إلى نقطة ثابتة، أي أنّه لا يمكن تغيير التجزئة بدون التراجع عن قرارات التجزئة السابقة.

يمكن تقسيم عملية النشر إلى خطوات. تتضمّن كل خطوة الاطّلاع على عملية معيّنة ونشرها بين مصفوفات (المُعامِلات والنتائج)، استنادًا إلى خصائص تلك العملية. على سبيل المثال، في دالة matmul، سننشر بين السمة غير المتعاقدة لأيٍّ من lhs أو rhs ل السمة المقابلة للنتيجة، أو بين السمة المتعاقدة لـ lhs وrhs.

تحدّد خصائص العملية الصلة بين السمات المقابلة في مدخلاتها ومخرجاتها، ويمكن تجميعها على أنّها قاعدة تقسيم لكلّ عملية.

في حال عدم حلّ التعارض، ستؤدي خطوة النشر إلى نشر أكبر عدد ممكن من القيم مع تجاهل المحاور المتعارضة، ويُشار إلى ذلك باسم المحاور (الأطول) المتوافقة مع تقسيم البيانات الرئيسي.

التصميم التفصيلي

التدرّج الهرمي لحلّ النزاعات

نضع استراتيجيات متعدّدة لحلّ النزاعات في تسلسل هرمي:

1. الأولويات التي يحدّدها المستخدم: في مقالة تمثيل التجزئة، شرحنا كيفية ربط الأولويات بتجزئة السمات للسماح بالتقسيم المتصاعد للبرنامج، مثل إجراء توازٍ بين الدفعات -> megatron -> تجزئة ZeRO. ويتم تحقيق ذلك من خلال تطبيق النشر في التكرارات. في المحاولةi، ننشر جميع تقسيمات السمات التي لها الأولوية<=i، ونغيّر كل العناصر الأخرى. نحرص أيضًا على أنّ عملية النشر لن تلغي عمليات تقسيم البيانات التي حدّدها المستخدم والتي لها أولوية أقل (>i)، حتى إذا تم تجاهلها أثناء النُسخ السابقة.
2. الأولويات المستندة إلى العمليات: ننشر عمليات التقسيم استنادًا إلى نوع المعالجة. تحظى عمليات "النقل المباشر" (مثل العمليات على مستوى العنصر وإعادة الشكل) بأعلى أولوية، في حين تحظى العمليات التي تتضمن تحويل الشكل (مثل dot وreduce) بأولوية أقل.
3. الانتشار السريع: انشر عمليات التقسيم باستخدام استراتيجية قوية. تنشر الاستراتيجية الأساسية عمليات تقسيم البيانات بدون تعارضات فقط، بينما تحلّ الاستراتيجية الهجومية التعارضات. يمكن أن يؤدي رفع مستوى الشدّة إلى تقليل مساحة الذاكرة التي يشغلها التطبيق، ولكن على حساب التواصل المحتمل.
4. النشر الأساسي: وهي أدنى استراتيجية للنشر في الهرم المشار إليه، ولا تُجري أي عملية حلّ للصراع، بل تنشر بدلاً من ذلك محاور متوافقة بين جميع المُعامِلات والنتائج.

يمكن تفسير هذا التسلسل الهرمي على أنّه حلقات for متداخلة. على سبيل المثال، لكل أولوية مستخدم، يتم تطبيق عملية نشر كاملة لأولوية التشغيل.

قاعدة تقسيم العمليات

تُقدّم قاعدة التجزئة نموذجًا مجردًا لكل عملية توفّر للخوارزمية الفعلية للنشر المعلومات التي تحتاجها لنشر التجزئات من المُعامِلات إلى النتائج أو على مستوى المُعامِلات، وما إلى ذلك، بدون الحاجة إلى التفكير في أنواع عمليات معيّنة وسمات هذه العمليات. ويعني ذلك في الأساس استبعاد المنطق الخاص بالعملية وتوفير تمثيل مشترَك (بنية البيانات) لجميع العمليات بغرض النشر فقط. في أبسط شكل لها، توفّر هذه الدالة فقط:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

تسمح لنا القاعدة بكتابة خوارزمية النشر مرة واحدة فقط بطريقة عامة تستند إلى بنية البيانات هذه (OpShardingRule)، بدلاً من تكرار أجزاء رمز مشابهة في العديد من العمليات، ما يقلل بشكل كبير من احتمالية حدوث أخطاء أو سلوك غير متسق في جميع العمليات.

لنعد إلى مثال matmul.

يمكن كتابة ترميز يلخّص المعلومات المطلوبة أثناء الانتشار، أي العلاقات بين السمات، في شكل رمز einsum:

(i, k), (k, j) -> (i, j)

في ترميز البيانات هذا، يتمّ ربط كلّ سمة بعامل واحد.

كيفية استخدام التوسيع لهذا الربط: إذا تم تجزئة سمة عامل حسابي/نتيجة على طول محور، سيبحث التوسيع عن عامل هذه السمة في هذا الربط، ويجزئ عوامل حسابية/نتائج أخرى على طول السمة الخاصة بها بالعامل نفسه، و (وفقًا للمناقشة السابقة حول النسخ) قد ينسخ أيضًا عوامل حسابية/نتائج أخرى لا تحتوي على هذا العامل على طول هذا المحور.

العوامل المركبة: توسيع نطاق تطبيق القاعدة على عمليات إعادة التنسيق

في العديد من العمليات، مثل matmul، ما عليك سوى ربط كل سمة بمتغيّر واحد . ومع ذلك، لا يكفي ذلك لإعادة التشكيل.

تدمج عملية إعادة التنسيق التالية سمتَين في سمة واحدة:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

تتطابق السمتَان 0 و1 من الإدخال مع السمة 0 من المخرجات. لنفترض أنّنا نبدأ بتقديم عوامل للمدخل:

(i,j,k) : i=2, j=4, k=32

يمكنك ملاحظة أنّه إذا أردنا استخدام العوامل نفسها في الإخراج، سنحتاج إلى سمة واحدة للإشارة إلى عوامل متعدّدة:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

يمكن إجراء الإجراء نفسه إذا كانت إعادة التنسيق ستؤدي إلى تقسيم سمة:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

يتكون سمة الحجم 8 هنا بشكل أساسي من العوامل 2 و4، لهذا السبب نسمي العوامل (i,j,k) عوامل.

يمكن أن تعمل هذه العوامل أيضًا في الحالات التي لا تتوفّر فيها سمة كاملة تتوافق مع أحد العوامل:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

يوضّح هذا المثال أيضًا سبب الحاجة إلى تخزين أحجام العوامل، لأنّه لا يمكننا استنتاجها بسهولة من الأبعاد المقابلة.

خوارزمية النشر الأساسية

نشر عمليات التجزئة على طول العوامل

في Shardy، لدينا التسلسل الهرمي للمتسلسلات الرباعية الأبعاد والسمات والعوامل. وهي تمثل البيانات على مستويات مختلفة. العامل هو سمة فرعية. وهو تسلسل هرمي داخلي يُستخدَم في نشر التجزئة. قد ترتبط كل سمة بعامل واحد أو أكثر. يتم تحديد التعيين بين السمة والعامل من خلال OpShardingRule.

تنشر Shardy محاور التجزئة على طول العوامل بدلاً من السمات. لتنفيذ ذلك، لدينا ثلاث خطوات كما هو موضّح في الشكل أدناه.

1. تغيير DimSharding في المشروع إلى FactorSharding
2. نشر محاور التجزئة في مساحة FactorSharding
3. توقع FactorSharding المعدَّل للحصول على DimSharding المعدَّل

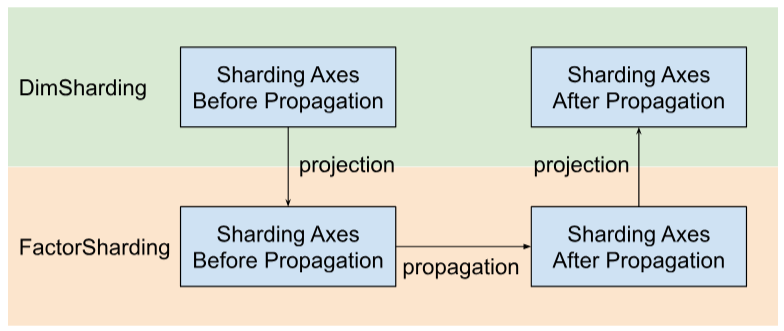
عرض مرئي لانتشار التجزئة على طول العوامل

سنستخدم الجدول التالي لعرض مشكلة انتشار التجزئة وآليتها.

	F0	F1	F2	المحاور التي تم تكرارها صراحةً
T0
T1
T2

• يمثّل كل عمود عاملاً. يشير F0 إلى العامل الذي يحمل الفهرس 0. ونقوم بنشر عمليات التقسيم على طول العوامل (الأعمدة).
• يمثّل كل صف مصفوفة كثيفة. يشير T0 إلى مصفوفة السلاسل الزمنية التي لها الفهرس 0. مصفوفات Tensor هي جميع المُعامِلات والنتائج المُدرَجة في عملية معيّنة. لا يمكن أن تتداخل المحاور في صف. لا يمكن استخدام محور (أو محور فرعي) لتقسيم كثافة واحدة متعدّدة مرات. إذا تم تكرار محور بشكل صريح، لا يمكننا استخدامه لمحاولة تقسيم المصفوفة.

وبالتالي، تمثّل كل خلية تقسيمًا للعوامل. يمكن أن يكون هناك عامل غير متوفّر في مكونات التوتر الجزئية. يمكنك الاطّلاع على الجدول أدناه.C = dot(A, B) تشير الخلايا التي تحتوي على N إلى أنّ العامل ليس في المتجه. على سبيل المثال، يكون F2 في T1 وT2، ولكن ليس في T0.

C = dot(A, B)	F0 Batching dim	F1 مستوى التعتيم غير المتغير	F2 تعتيم غير متقلّص	F3 تعتيم متضائل	المحاور التي تم تكرارها بشكل صريح
T0 = A			لا
T1 = B		لا
T2 = C				لا

جمع محاور التجزئة ونشرها

سنستخدم مثالاً بسيطًا موضحًا أدناه لعرض عملية النشر.

	F0	F1	F2	المحاور التي تم تكرارها صراحةً
T0	"a"		"f"
T1	"a", "b"	"ج"، "د"	"g"
T2		"ج"، "هـ"

الخطوة 1: ابحث عن المحاور التي تريد نشرها على طول كل عامل (المعروفة أيضًا باسم محاور التجزئة الرئيسية (الأطول) المتوافقة). في هذا المثال، ننشر ["a", "b"] على طول F0، وننشر ["c"] على طول F1، ولا ننشر أيّ قيمة على طول F2.

الخطوة 2: وسِّع تقسيمات العوامل للحصول على النتيجة التالية.

	F0	F1	F2	المحاور التي تم تكرارها صراحةً
T0	"أ"، "ب"	"c"	"f"
T1	"a", "b"	"ج"، "د"	"g"
T2	"a", "b"	"ج"، "هـ"