דף זה תורגם על ידי Cloud Translation API.

התפשטות
קל לארגן דפים בעזרת אוספים אפשר לשמור ולסווג תוכן על סמך ההעדפות שלך.

סקירה כללית

בהפצה של חלוקה למקטעים, המערכת משתמשת בחלוקות למקטעים שהמשתמשים ציינו כדי להסיק את החלוקות למקטעים של הטנזורים (או של מאפיין ספציפי של הטנזורים) שלא צוינו. הוא חוצה את זרימת הנתונים (שרשראות של הגדרות שימוש) של תרשים החישוב בשני הכיוונים עד שמגיעים לנקודה קבועה, כלומר, כבר אי אפשר לשנות את החלוקה לחלקים בלי לבטל את ההחלטות הקודמות לגבי חלוקה לחלקים.

אפשר לפרק את ההעברה לשלבים. כל שלב כולל בדיקה של פעולה ספציפית והעברה בין טינסורים (אופרטנדים ותוצאות), על סמך המאפיינים של הפעולה. לדוגמה, אם מדובר ב-matmul, נפיץ בין המאפיין שאינו מתכווץ של lhs או של rhs למאפיין התואם של התוצאה, או בין המאפיין המתכווץ של lhs ושל rhs.

המאפיינים של פעולה קובעים את הקשר בין המאפיינים התואמים בקלט ובפלט שלה, וניתן להכליל אותם ככלל חלוקה (sharding) לכל פעולה.

בלי פתרון התנגשויות, שלב ההעברה (propagation) פשוט יפרס כמה שיותר נתונים תוך התעלמות מהצירים שנמצאים בהתנגשות. אנחנו מתייחסים לכך בתור צירי הפיצול הראשיים (הארוכים ביותר) התואמים.

תכנון מפורט

היררכיית פתרון התנגשויות

אנחנו משלבים כמה אסטרטגיות לפתרון סכסוכים בהיררכיה:

עדיפויות מוגדרות על ידי משתמש. במאמר Sharding Representation, תיארנו איך אפשר לצרף תעדוף לפי חלוקה של מאפיינים כדי לאפשר חלוקה מצטברת של התוכנית, למשל, ביצוע מקביליות באצווה –>‏ megatron –>‏ חלוקה לפי ZeRO. כדי לעשות זאת, אנחנו מחילים את ההעברה (propagation) בחזרות (iterations) – בחזרה i אנחנו מעבירים את כל חלוקות המאפיינים שיש להן עדיפות <=i ומתעלים מכל שאר החלוקות. אנחנו גם מוודאים שההפצה לא תשנה חלוקות (shards) מוגדרות על ידי משתמשים עם עדיפות נמוכה יותר (>i), גם אם התעלמו מהן במהלך איטרציות קודמות.
עדיפויות מבוססות-פעולה. אנחנו מפיצים את החלוקה לחלקים על סמך סוג הפעולה. לפעולות 'מעבר' (למשל, פעולות לפי רכיבים ושינוי צורה) יש את העדיפות הגבוהה ביותר, ולפעולות עם טרנספורמציה של צורה (למשל, dot ו-reduce) יש עדיפות נמוכה יותר.
העברה אגרסיבית להפיץ את החלוקה לפלחים באמצעות אסטרטגיה אגרסיבית. האסטרטגיה הבסיסית מפיצה רק חלוקות ללא התנגשויות, ואילו האסטרטגיה האגרסיבית פותרת את ההתנגשויות. רמת אגרסיביות גבוהה יותר יכולה לצמצם את טביעת הרגל של הזיכרון, אבל על חשבון תקשורת פוטנציאלית.
העברה בסיסית זוהי אסטרטגיית ההעברה הנמוכה ביותר בהיררכיה, שלא מבצעת פתרון של התנגשויות, ובמקום זאת מעבירה צירים שתואמים לכל המשתנים והתוצאות.

היררכיית ההעברה, שמציגה 4 סטאקים, מלמטה למעלה, עם התוויות הבאות: Basic Propagation,‏ Aggressive Propagation,‏ Operation Priority Propagation ו-User Priority Propagation.

אפשר לפרש את ההיררכיה הזו כמחזורים בתצוגת עץ. לדוגמה, לכל עדיפות משתמש מוחל העברה מלאה של עדיפות הפעולה.

כלל חלוקה של פעולות

כלל הפיצול מאפשר ליצור הפשטה של כל פעולה, שמספקת לאלגוריתם ההעברה בפועל את המידע הדרוש להעברת הפיצולים מאופרטורים לתוצאות או בין אופרטורים, בלי צורך להסיק מסקנות לגבי סוגי פעולות ספציפיים והמאפיינים שלהם. בעיקרון, מדובר בהוצאה של הלוגיקה הספציפית של הפעולה ומתן ייצוג משותף (מבנה נתונים) לכל הפעולות למטרות העברה בלבד. בצורתה הפשוטה ביותר, היא מספקת רק את הפונקציה הזו:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

הכלל מאפשר לנו לכתוב את אלגוריתם ההפצה רק פעם אחת באופן כללי שמבוסס על מבנה הנתונים הזה (OpShardingRule), במקום לשכפל קטעי קוד דומים במספר רב של פעולות, וכך לצמצם באופן משמעותי את האפשרות לבאגים או להתנהגות לא עקבית בין הפעולות.

נחזור לדוגמה של matmul.

אפשר לכתוב קידוד שמכיל את המידע הנדרש במהלך ההעברה, כלומר היחסים בין המאפיינים, בצורת סימון einsum:

(i, k), (k, j) -> (i, j)

בקידוד הזה, כל מאפיין ממופה לגורם יחיד.

איך ההעברה משתמשת במיפוי הזה: אם מאפיין של אופרטור/תוצאה מחולק לפלחים לאורך ציר, ההעברה תבדוק את הגורם של המאפיין הזה במיפוי הזה, ותחלק לפלחים אופרטורים/תוצאות אחרים לאורך המאפיין המתאים שלהם עם אותו גורם – ועשויה גם לשכפל אופרטורים/תוצאות אחרים שאין להם את הגורם הזה לאורך הציר הזה (בהתאם לדיון הקודם על שכפול).

גורמים מורכבים: הרחבת הכלל לשינוי צורת הנתונים

בפעולות רבות, למשל matmul, צריך למפות כל מאפיין רק לגורם אחד. עם זאת, הוא לא מספיק לשינוי הצורה.

הפונקציה הבאה לשינוי הצורה משלבת שני מאפיינים למאפיין אחד:

%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

כאן, גם המאפיין 0 וגם המאפיין 1 של הקלט תואמים למאפיין 0 של הפלט. נניח שמתחילים על ידי מתן גורמים לקלט:

(i,j,k) : i=2, j=4, k=32

אפשר לראות שאם רוצים להשתמש באותם גורמים בפלט, צריך מאפיין אחד שיפנה לכמה גורמים:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

אפשר לעשות את אותו הדבר אם שינוי הצורה גורם לפיצול של מאפיין:

%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>

כאן,

((ij), k) -> (i,j,k) : i=2, j=4, k=32

המאפיין בגודל 8 מורכב בעיקר מהגורמים 2 ו-4, ולכן אנחנו קוראים לגורמים האלה גורמי (i,j,k).

הגורמים האלה יכולים לפעול גם במקרים שבהם אין מאפיין מלא שתואם לאחד מהגורמים:

%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

הדוגמה הזו מדגישה גם למה אנחנו צריכים לאחסן את גורמי הגודל – כי אי אפשר להסיק אותם בקלות מהמאפיינים המתאימים.

אלגוריתם העברה ליבה

העברת חלוקות לפי גורמים

ב-Shardy יש היררכיה של טינסורים, מאפיינים וגורמים. הם מייצגים נתונים ברמות שונות. גורם הוא מאפיין משני. זוהי היררכיה פנימית שמשמשת להפצה של חלוקה לקטעים. כל מאפיין יכול להתאים לגורם אחד או יותר. המיפוי בין המאפיין לגורם מוגדר על ידי OpShardingRule.

סכימה שמציגה את אלגוריתם ההפצה של Shardy.

Shardy מעביר את צירי הפיצול לפי גורמים במקום לפי מאפיינים. כדי לעשות זאת, יש לנו שלושה שלבים, כפי שמוצג באיור הבא:

פרויקט DimSharding עד FactorSharding
הפיכת צירי חלוקה לזמינים במרחב של FactorSharding
מקרינים את FactorSharding המעודכן כדי לקבל את DimSharding המעודכן

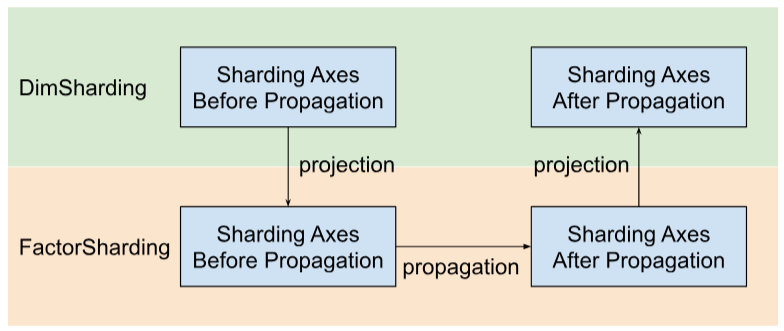
סכימה שמראה את ההפצה של חלוקה לקטעים ב-FactorSharding וב-DimSharding.

תצוגה חזותית של ההפצה של חלוקה לקטעים לפי גורמים

נשתמש בטבלה הבאה כדי להמחיש את הבעיה ואת האלגוריתם של ההפצה באמצעות חלוקה לקטעים.

	F0	F1	F2	צירים שמתבצעת להם רפליקה באופן מפורש
T0
T1
T2

כל עמודה מייצגת גורם. F0 הוא הגורם עם האינדקס 0. אנחנו מפיצים את החלוקה לגורמים (עמודות).
כל שורה מייצגת טינסור. T0 מתייחס לטרנספורמר עם האינדקס 0. טינסורים הם כל המשתנים והתוצאות שקשורים לפעולה ספציפית. הצירים בשורה לא יכולים לחפוף. אי אפשר להשתמש בציר (או בציר משנה) כדי לפצל טינסור אחד פעמים רבות. אם ציר מסוים מוכפל באופן מפורש, אי אפשר להשתמש בו כדי לפצל את הטנזור.

לכן, כל תא מייצג חלוקה של גורם. יכול להיות שגורם חסר בטנסורים חלקיים. בטבלה שבהמשך מופיע הערך של C = dot(A, B). התאים שמכילים את הערך N מצביעים על כך שהגורם לא נמצא בטנסור. לדוגמה, F2 נמצא ב-T1 וב-T2, אבל לא ב-T0.

`C = dot(A, B)`	מאפיין F1 ללא חוזה	F2 Non-contracting dim	F3 Contracting dim
T0 = A		לא
T1 = B	לא
T2 = C			לא

איסוף והפצה של צירי חלוקה

כדי להמחיש את ההעברה, נשתמש בדוגמה פשוטה שמופיעה בהמשך.

	F0	F1	F2
T0	‎"a"‎		‎"f"‎
T1	"a",‏ "b"	'c',‏ 'd'	'g'
T2		'c',‏ 'e'

שלב 1. חיפוש צירים להעברה לאורך כל גורם (כלומר, צירי הפיצול הראשיים (הארוכים ביותר) שתואמים). בדוגמה הזו, אנחנו מעבירים את ["a", "b"] לאורך F0, מעבירים את ["c"] לאורך F1 ולא מעבירים דבר לאורך F2.

שלב 2. מרחיבים את חלוקות הגורמים כדי לקבל את התוצאה הבאה.

	F0	F1	F2
T0	'a', ‏ 'b'	"c"	‎"f"‎
T1	"a",‏ "b"	'c',‏ 'd'	'g'
T2	"a", "b"	'c',‏ 'e'

פעולות של זרימת נתונים

התיאור של שלב ההפצה שלמעלה רלוונטי לרוב הפעולות. עם זאת, יש מקרים שבהם כלל חלוקה לא מתאים. במקרים כאלה, Shardy מגדיר אופרטורים של זרימת נתונים.

קצה של זרימת נתונים של פעולה X מסוימת מגדיר גשר בין קבוצה של מקורות לבין קבוצה של יעדים, כך שכל המקורות והיעדים צריכים להיות מחולקים לפלחים באותו אופן. דוגמאות לפעולות כאלה הן stablehlo::OptimizationBarrierOp,‏ stablehlo::WhileOp, ‏ stablehlo::CaseOp וגם sdy::ManualComputationOp. בסופו של דבר, כל פעולה שמטמיעה את ShardableDataFlowOpInterface נחשבת לפעולה של תעבורת נתונים.

לפעולה יכולים להיות כמה צמתים של זרימת נתונים שמקבילים זה לזה. לדוגמה:

    y_0, ..., y_n = while (x_0, ..., x_n)
                    ((pred_arg_0,... , pred_arg_n) { ... })
                    ((body_arg_0,..., body_arg_n) {
                    ...
                    return return_value_0, ..., return_value_n
                    })

לפעולה הזו של 'בזמן ש' יש n צמתים של זרימת נתונים: הצומת ה-i של זרימת הנתונים הוא בין המקורות x_i, ‏ return_value_i לבין היעדים y_i, ‏ pred_arg_i, ‏ body_arg_i.

Shardy יפיץ את החלוקה לחלקים בין כל המקורות והיעדים של קצה של תהליך העברת נתונים, כאילו מדובר בפעולה רגילה שבה המקורות משמשים כאופרטורים והיעדים משמשים כתוצאות, ויש זהות sdy.op_sharding_rule. כלומר, העברה קדימה היא מהמקורות ליעדים, והעברה אחורה היא מהיעדים למקורות.

המשתמש צריך להטמיע כמה שיטות שמתארות איך לקבל את המקורות והיעדים של כל קצוות זרימת הנתונים דרך הבעלים שלהם, וגם איך לקבל ולהגדיר את החלוקות של הבעלים של הקצוות. הבעלים הוא יעד שצוין על ידי המשתמש של קצה זרימת הנתונים שמשמש את ההפצה של Shardy. המשתמש יכול לבחור אותו באופן שרירותי, אבל הוא צריך להיות סטטי.

לדוגמה, בהתאם להגדרה הבאה של custom_op:

  y_1, ..., y_n = custom_op (x_1, ..., x_n)
                  ((body_arg_1,..., body_arg_n) {
                    ...
                    return return_value_1, ..., return_value_n
                  })

ל-custom_op יש שני סוגים של צמתים של זרימת נתונים: n צמתים בין return_value_i (מקורות) ל-y_i (יעדים), ו-n צמתים בין x_i (מקורות) ל-body_arg_i (יעדים). במקרה כזה, בעלי הקצוות הם אותם יעדים.

התפשטות קל לארגן דפים בעזרת אוספים אפשר לשמור ולסווג תוכן על סמך ההעדפות שלך.