Penerapan

Ringkasan

Penyebaran sharding menggunakan sharding yang ditentukan pengguna untuk menyimpulkan sharding tensor yang tidak ditentukan (atau dimensi tensor tertentu). Algoritma ini melintasi alur data (rantai use-def) dari grafik komputasi di kedua arah hingga titik tetap tercapai, yaitu, sharding tidak dapat lagi berubah tanpa mengurungkan keputusan sharding sebelumnya.

Penyebaran dapat diuraikan menjadi beberapa langkah. Setiap langkah melibatkan melihat operasi tertentu dan menyebarkan antara tensor (operand dan hasil), berdasarkan karakteristik operasi tersebut. Dengan mengambil matmul sebagai contoh, kita akan menyebarkan antara dimensi non-kontrak dari lhs atau rhs ke dimensi hasil yang sesuai, atau antara dimensi kontrak dari lhs dan rhs.

Karakteristik operasi menentukan koneksi antara dimensi yang sesuai dalam input dan outputnya, dan dapat diringkas sebagai aturan sharding per operasi.

Tanpa resolusi konflik, langkah penyebaran hanya akan menyebarkan sebanyak mungkin sambil mengabaikan sumbu yang bertentangan; kami menyebutnya sebagai sumbu sharding utama (terpanjang) yang kompatibel.

Desain Terperinci

Hierarki resolusi konflik

Kita menyusun beberapa strategi resolusi konflik dalam hierarki:

1. Prioritas yang ditentukan pengguna. Dalam Perwakilan Sharding, kami menjelaskan cara prioritas dapat dilampirkan ke sharding dimensi untuk memungkinkan partisi progresif program, misalnya, melakukan paralelisme batch -> megatron -> sharding ZeRO. Hal ini dicapai dengan menerapkan propagasi dalam iterasi - pada iterasi i, kita akan menyebarkan semua sharding dimensi yang memiliki prioritas <=i dan mengabaikan semua yang lain. Kami juga memastikan bahwa propagasi tidak akan mengganti sharding yang ditentukan pengguna dengan prioritas yang lebih rendah (>i), meskipun diabaikan selama iterasi sebelumnya.
2. Prioritas berbasis operasi. Kami menyebarkan sharding, berdasarkan jenis operasi. Operasi “pass-through” (misalnya, operasi per elemen dan pembentukan ulang) memiliki prioritas tertinggi, sedangkan operasi dengan transformasi bentuk (misalnya, titik dan kurangi) memiliki prioritas yang lebih rendah.
3. Penyebaran yang agresif. Memperluas sharding dengan strategi agresif. Strategi dasar hanya menyebarkan sharding tanpa konflik, sedangkan strategi agresif menyelesaikan konflik. Agresivitas yang lebih tinggi dapat mengurangi jejak memori dengan mengorbankan potensi komunikasi.
4. Penyebaran Dasar. Ini adalah strategi propagasi terendah dalam hierarki, yang tidak melakukan resolusi konflik apa pun, dan sebagai gantinya menyebarkan sumbu yang kompatibel di antara semua operand dan hasil.

Hierarki ini dapat ditafsirkan sebagai loop for bertingkat. Misalnya, untuk setiap prioritas pengguna, propagasi prioritas op penuh diterapkan.

Aturan sharding operasi

Aturan sharding memperkenalkan abstraksi dari setiap operasi yang menyediakan algoritme penyebaran sebenarnya dengan informasi yang diperlukan untuk menyebarkan sharding dari operand ke hasil atau di seluruh operand, dll., tanpa harus membuat alasan tentang jenis operasi tertentu dan atributnya. Hal ini pada dasarnya memfaktorkan logika khusus op dan memberikan representasi bersama (struktur data) untuk semua op hanya untuk tujuan penyebaran. Dalam bentuk paling sederhana, fungsi ini hanya menyediakan fungsi ini:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

Aturan ini memungkinkan kita menulis algoritma penyebaran hanya sekali dengan cara umum yang didasarkan pada struktur data ini (OpShardingRule), bukan mereplikasi bagian kode yang serupa di banyak operasi, sehingga sangat mengurangi kemungkinan bug atau perilaku yang tidak konsisten di seluruh operasi.

Mari kita kembali ke contoh matmul.

Encoding yang mengenkapsulasi informasi yang diperlukan selama propagasi, yaitu hubungan antardimensi, dapat ditulis dalam bentuk notasi einsum:

(i, k), (k, j) -> (i, j)

Dalam encoding ini, setiap dimensi dipetakan ke satu faktor.

Cara penyebaran menggunakan pemetaan ini: Jika dimensi operand/hasil di-shard di sepanjang sumbu, penyebaran akan mencari faktor dimensi tersebut dalam pemetaan ini, dan me-shard operand/hasil lain di sepanjang dimensi masing-masing dengan faktor yang sama – dan (tunduk pada diskusi sebelumnya tentang replikasi) mungkin juga mereplikasi operand/hasil lain yang tidak memiliki faktor tersebut di sepanjang sumbu tersebut.

Faktor gabungan: memperluas aturan untuk pembentukan ulang

Dalam banyak operasi, misalnya, matmul, kita hanya perlu memetakan setiap dimensi ke satu faktor. Namun, ini tidak cukup untuk mengubah bentuk.

Pembentukan ulang berikut menggabungkan dua dimensi menjadi satu:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

Di sini, dimensi 0 dan 1 input sesuai dengan dimensi 0 output. Misalnya, kita mulai dengan memberikan faktor ke input:

(i,j,k) : i=2, j=4, k=32

Anda dapat melihat bahwa jika ingin menggunakan faktor yang sama untuk output, kita akan memerlukan satu dimensi untuk mereferensikan beberapa faktor:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

Hal yang sama dapat dilakukan jika pembentukan ulang akan memisahkan dimensi:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

Dimensi ukuran 8 di sini pada dasarnya terdiri dari faktor 2 dan 4, yang menjadi alasan kami menyebut faktor (i,j,k).

Faktor ini juga dapat berfungsi jika tidak ada dimensi lengkap yang sesuai dengan salah satu faktor:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Contoh ini juga menekankan alasan kita perlu menyimpan ukuran faktor - karena kita tidak dapat dengan mudah menyimpulkannya dari dimensi yang sesuai.

Algoritma Penyebaran Inti

Memperluas sharding berdasarkan faktor

Di Shardy, kita memiliki hierarki tensor, dimensi, dan faktor. Model tersebut mewakili data di berbagai tingkat. Faktor adalah sub-dimensi. Ini adalah hierarki internal yang digunakan dalam propagasi sharding. Setiap dimensi dapat sesuai dengan satu atau beberapa faktor. Pemetaan antara dimensi dan faktor ditentukan oleh OpShardingRule.

Shardy menyebarkan sumbu sharding di sepanjang faktor, bukan dimensi. Untuk melakukannya, kita memiliki tiga langkah seperti yang ditunjukkan pada gambar di bawah ini

1. Memindahkan DimSharding Project ke FactorSharding
2. Memperluas sumbu sharding di ruang FactorSharding
3. Proyeksikan FactorSharding yang diperbarui untuk mendapatkan DimSharding yang diperbarui

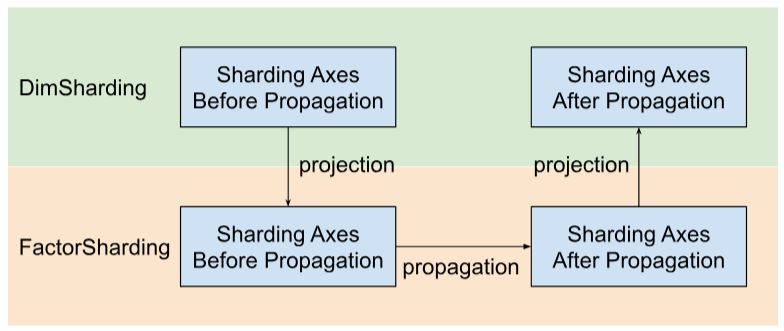
Visualisasi Penyebaran Sharding Menurut Faktor

Kita akan menggunakan tabel berikut untuk memvisualisasikan masalah dan algoritma penyebaran sharding.

	F0	F1	F2	Sumbu yang direplikasi secara eksplisit
T0
T1
T2

• Setiap kolom mewakili faktor. F0 berarti faktor dengan indeks 0. Kami memperluas sharding di sepanjang faktor (kolom).
• Setiap baris mewakili tensor. T0 mengacu pada tensor dengan indeks 0. Tensor adalah semua operand dan hasil yang terlibat untuk operasi tertentu. Sumbu dalam baris tidak boleh tumpang tindih. Sumbu (atau sub-sumbu) tidak dapat digunakan untuk mempartisi satu tensor beberapa kali. Jika sumbu direplikasi secara eksplisit, kita tidak dapat menggunakannya untuk mempartisi tensor.

Dengan demikian, setiap sel mewakili sharding faktor. Faktor dapat tidak ada dalam tensor sebagian. Tabel untuk C = dot(A, B) ada di bawah. Sel yang berisi N menyiratkan bahwa faktor tidak ada dalam tensor. Misalnya, F2 ada di T1 dan T2, tetapi tidak ada di T0.

C = dot(A, B)	Redup Pengelompokan F0	F1 Redup non-kontraksi	F2 Redup non-kontraksi	F3 Kontrak redup	Sumbu yang direplikasi secara eksplisit
T0 = A			T
T1 = B		T
T2 = C				T

Mengumpulkan dan menyebarkan sumbu sharding

Kita menggunakan contoh sederhana yang ditampilkan di bawah untuk memvisualisasikan propagasi.

	F0	F1	F2	Sumbu yang direplikasi secara eksplisit
T0	"a"		"f"
T1	"a", "b"	"c", "d"	"g"
T2		"c", "e"

Langkah 1. Temukan sumbu untuk disebarkan di sepanjang setiap faktor (alias sumbu sharding utama (terpanjang) yang kompatibel). Untuk contoh ini, kita menyebarkan ["a", "b"] di sepanjang F0, menyebarkan ["c"] di sepanjang F1, dan tidak menyebarkan apa pun di sepanjang F2.

Langkah 2. Luaskan sharding faktor untuk mendapatkan hasil berikut.

	F0	F1	F2	Sumbu yang direplikasi secara eksplisit
T0	"a", "b"	"c"	"f"
T1	"a", "b"	"c", "d"	"g"
T2	"a", "b"	"c", "e"