Truyền tải

Tổng quan

Quá trình phân đoạn truyền tải sử dụng các phân đoạn do người dùng chỉ định để suy luận các phân đoạn chưa chỉ định của tensor (hoặc phương diện cụ thể của tensor). Phương thức này sẽ di chuyển qua luồng dữ liệu (chuỗi use-def) của biểu đồ tính toán theo cả hai hướng cho đến khi đạt đến một điểm cố định, tức là không thể phân đoạn nữa mà không huỷ các quyết định phân đoạn trước đó.

Bạn có thể phân ly quá trình truyền tải thành các bước. Mỗi bước bao gồm việc xem xét một toán tử cụ thể và truyền tải giữa các tensor (toán hạng và kết quả), dựa trên các đặc điểm của toán tử đó. Lấy matmul làm ví dụ, chúng ta sẽ truyền giữa kích thước không co rút của lhs hoặc rhs đến kích thước tương ứng của kết quả, hoặc giữa kích thước co rút của lhs và rhs.

Các đặc điểm của một toán tử xác định mối liên kết giữa các phương diện tương ứng trong dữ liệu đầu vào và đầu ra của toán tử đó, đồng thời có thể được trừu tượng hoá dưới dạng một quy tắc phân đoạn cho mỗi toán tử.

Nếu không có tính năng phân giải xung đột, một bước truyền tải sẽ chỉ truyền tải nhiều nhất có thể trong khi bỏ qua các trục xung đột; chúng tôi gọi đây là trục phân đoạn chính tương thích (dài nhất).

Thiết kế chi tiết

Hệ phân cấp giải quyết xung đột

Chúng ta sẽ soạn nhiều chiến lược giải quyết xung đột theo hệ phân cấp:

1. Mức độ ưu tiên do người dùng xác định. Trong phần Đại diện phân đoạn, chúng tôi đã mô tả cách đính kèm các mức độ ưu tiên vào các phân đoạn kích thước để cho phép phân vùng tăng dần của chương trình, ví dụ: thực hiện song song hàng loạt -> megatron -> phân đoạn ZeRO. Điều này được thực hiện bằng cách áp dụng tính năng truyền trong các vòng lặp – tại vòng lặp i, chúng ta truyền tất cả các phân đoạn thứ nguyên có mức độ ưu tiên <=i và bỏ qua tất cả các phân đoạn khác. Chúng tôi cũng đảm bảo rằng quá trình truyền tải sẽ không ghi đè các phân đoạn do người dùng xác định có mức độ ưu tiên thấp hơn (>i), ngay cả khi các phân đoạn đó bị bỏ qua trong các lần lặp lại trước đó.
2. Mức độ ưu tiên dựa trên hoạt động. Chúng tôi sẽ truyền tải các phân đoạn dựa trên loại thao tác. Các thao tác "chuyển tiếp" (ví dụ: thao tác theo phần tử và định hình lại) có mức độ ưu tiên cao nhất, trong khi các thao tác có phép biến đổi hình dạng (ví dụ: dấu chấm và giảm) có mức độ ưu tiên thấp hơn.
3. Phát tán mạnh mẽ. Truyền tải các phân đoạn bằng chiến lược tích cực. Chiến lược cơ bản chỉ truyền bá các phân đoạn không có xung đột, trong khi chiến lược tích cực sẽ giải quyết xung đột. Độ tích cực cao hơn có thể làm giảm mức sử dụng bộ nhớ nhưng sẽ làm giảm khả năng giao tiếp tiềm năng.
4. Phát tán cơ bản. Đây là chiến lược truyền tải thấp nhất trong hệ phân cấp, không giải quyết xung đột nào và thay vào đó, truyền tải các trục tương thích giữa tất cả toán hạng và kết quả.

Hệ phân cấp này có thể được hiểu là các vòng lặp for lồng nhau. Ví dụ: đối với mỗi mức độ ưu tiên của người dùng, hệ thống sẽ áp dụng việc truyền mức độ ưu tiên hoạt động đầy đủ.

Quy tắc phân đoạn hoạt động

Quy tắc phân đoạn giới thiệu một bản tóm tắt về mọi thao tác cung cấp cho thuật toán truyền tải thực tế thông tin cần thiết để truyền tải các phân đoạn từ toán hạng đến kết quả hoặc trên các toán hạng, v.v. mà không cần phải suy luận về các loại thao tác cụ thể và thuộc tính của các thao tác đó. Về cơ bản, việc này là phân tích logic dành riêng cho toán tử và cung cấp một bản trình bày dùng chung (cấu trúc dữ liệu) cho tất cả các toán tử chỉ nhằm mục đích truyền tải. Ở dạng đơn giản nhất, lớp này chỉ cung cấp hàm sau:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

Quy tắc này cho phép chúng ta chỉ viết thuật toán truyền tải một lần theo cách chung dựa trên cấu trúc dữ liệu này (OpShardingRule), thay vì sao chép các đoạn mã tương tự trên nhiều thao tác, giúp giảm đáng kể khả năng xảy ra lỗi hoặc hành vi không nhất quán trên các thao tác.

Hãy quay lại ví dụ về matmul.

Bạn có thể viết một mã hoá đóng gói thông tin cần thiết trong quá trình truyền tải (tức là các mối quan hệ giữa các phương diện) ở dạng ký hiệu einsum:

(i, k), (k, j) -> (i, j)

Trong quá trình mã hoá này, mỗi phương diện được liên kết với một yếu tố duy nhất.

Cách quá trình nhân rộng sử dụng ánh xạ này: Nếu một phương diện của toán hạng/kết quả được phân đoạn dọc theo một trục, thì quá trình nhân rộng sẽ tra cứu hệ số của phương diện đó trong ánh xạ này và phân đoạn các toán hạng/kết quả khác dọc theo phương diện tương ứng của chúng bằng cùng một hệ số – và (theo nội dung thảo luận trước đó về tính năng sao chép) cũng có thể sao chép các toán hạng/kết quả khác không có hệ số đó dọc theo trục đó.

Các hệ số phức hợp: mở rộng quy tắc cho việc định hình lại

Trong nhiều toán tử, ví dụ: matmul, chúng ta chỉ cần ánh xạ mỗi phương diện đến một hệ số duy nhất. Tuy nhiên, điều này là chưa đủ đối với việc định hình lại.

Hàm định hình lại sau đây hợp nhất hai phương diện thành một:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

Ở đây, cả phương diện 0 và 1 của dữ liệu đầu vào đều tương ứng với phương diện 0 của dữ liệu đầu ra. Giả sử chúng ta bắt đầu bằng cách cung cấp các hệ số cho dữ liệu đầu vào:

(i,j,k) : i=2, j=4, k=32

Bạn có thể thấy rằng nếu muốn sử dụng cùng một yếu tố cho kết quả, chúng ta sẽ cần một phương diện duy nhất để tham chiếu nhiều yếu tố:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

Bạn cũng có thể thực hiện tương tự nếu việc định hình lại là để tách một phương diện:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

Phương diện kích thước 8 ở đây về cơ bản bao gồm các hệ số 2 và 4, đó là lý do chúng ta gọi các hệ số này là hệ số (i,j,k).

Các yếu tố này cũng có thể hoạt động trong trường hợp không có phương diện đầy đủ tương ứng với một trong các yếu tố:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Ví dụ này cũng nhấn mạnh lý do chúng ta cần lưu trữ kích thước hệ số – vì chúng ta không thể dễ dàng suy ra các kích thước đó từ các kích thước tương ứng.

Thuật toán truyền dẫn lõi

Truyền tải các phân đoạn theo các yếu tố

Trong Shardy, chúng ta có hệ phân cấp tensor, phương diện và hệ số. Các chỉ số này đại diện cho dữ liệu ở các cấp độ khác nhau. Yếu tố là một phương diện phụ. Đây là một hệ phân cấp nội bộ dùng trong việc truyền tải phân đoạn. Mỗi phương diện có thể tương ứng với một hoặc nhiều yếu tố. Việc ánh xạ giữa phương diện và hệ số được xác định bởi OpShardingRule.

Shardy truyền tải các trục phân đoạn theo các yếu tố thay vì các phương diện. Để làm điều đó, chúng ta có 3 bước như minh hoạ trong hình bên dưới

1. Dự án DimSharding thành FactorSharding
2. Truyền các trục phân đoạn trong không gian của FactorSharding
3. Dự án FactorSharding đã cập nhật để nhận DimSharding đã cập nhật

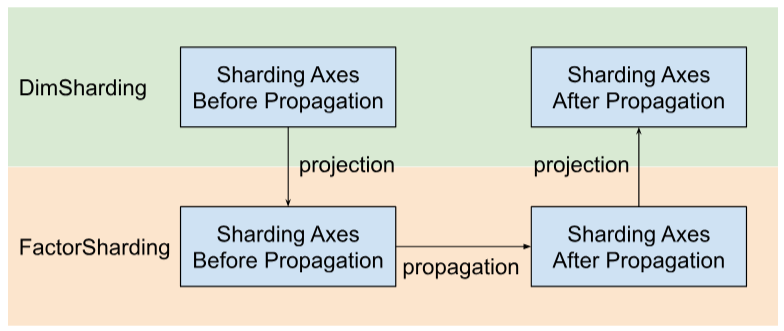
Hình ảnh minh hoạ việc truyền tải phân đoạn theo các yếu tố

Chúng ta sẽ sử dụng bảng sau để minh hoạ thuật toán và vấn đề truyền tải phân đoạn.

	F0	F1	F2	Trục được sao chép rõ ràng
T0
T1
T2

• Mỗi cột đại diện cho một yếu tố. F0 có nghĩa là hệ số có chỉ mục 0. Chúng ta sẽ phân tán theo các yếu tố (cột).
• Mỗi hàng đại diện cho một tensor. T0 đề cập đến tensor có chỉ mục 0. Tensor là tất cả các toán hạng và kết quả liên quan đến một phép toán cụ thể. Các trục trong một hàng không được chồng chéo nhau. Không thể sử dụng một trục (hoặc trục phụ) để phân vùng một tensor nhiều lần. Nếu một trục được sao chép một cách rõ ràng, chúng ta không thể sử dụng trục đó để phân vùng tensor.

Do đó, mỗi ô đại diện cho một phân đoạn hệ số. Một hệ số có thể bị thiếu trong các tensor một phần. Dưới đây là bảng cho C = dot(A, B). Các ô chứa N cho biết rằng hệ số này không có trong tensor. Ví dụ: F2 nằm trong T1 và T2, nhưng không nằm trong T0.

C = dot(A, B)	F0 Tối theo lô	F1 Tắt sáng không co lại	F2 Tắt sáng không co lại	F3 Hiệu ứng làm mờ khi thu nhỏ	Trục được sao chép rõ ràng
T0 = A			Không
T1 = B		Không
T2 = C				Không

Thu thập và truyền tải các trục phân đoạn

Chúng ta sử dụng một ví dụ đơn giản như bên dưới để minh hoạ quá trình truyền tin.

	F0	F1	F2	Trục được sao chép rõ ràng
T0	"a"		"f"
T1	"a", "b"	"c", "d"	"g"
T2		"c", "e"

Bước 1. Tìm các trục để truyền tải dọc theo từng yếu tố (còn gọi là trục phân đoạn chính (dài nhất) tương thích). Trong ví dụ này, chúng ta truyền ["a", "b"] dọc theo F0, truyền ["c"] dọc theo F1 và không truyền gì dọc theo F2.

Bước 2. Mở rộng các phân đoạn theo hệ số để có được kết quả sau.

	F0	F1	F2	Trục được sao chép rõ ràng
T0	"a", "b"	"c"	"f"
T1	"a", "b"	"c", "d"	"g"
T2	"a", "b"	"c", "e"