總覽
區塊傳播會使用使用者指定的區塊,推斷未指定的張量區塊 (或張量的特定維度)。它會在兩個方向上遍歷運算圖的資料流程 (使用定義鏈結),直到達到固定點為止,也就是說,如果不撤銷先前的區隔決策,區隔就無法再變更。
傳播作業可分解為多個步驟。每個步驟都會根據該運算的特性,查看特定運算並在張量 (運算元和結果) 之間傳播。以 matmul 為例,我們會在左側或右側的非收縮維度之間,傳播至結果的對應維度,或是在左側和右側的收縮維度之間。
運算的特性會決定輸入和輸出內容中相應維度的連結,並可抽象化為每個運算的分割規則。
如果沒有衝突解析,傳播步驟會盡可能傳播,同時忽略衝突的軸線;我們稱之為 (最長) 相容的主要區隔軸。
縝密設計
衝突解決階層
我們在階層中組合多種衝突解決策略:
- 使用者定義的優先順序。在「分割表示法」一文中,我們說明瞭如何將優先順序附加至維度分割作業,以便逐步分割程式,例如執行批次並行處理 -> megatron -> ZeRO 分割作業。這可透過在迭代中套用傳播方式達成,在迭代
i時,我們會傳播所有具有優先順序<=i的維度分割,並忽略所有其他維度分割。我們也確保傳播不會覆寫使用者定義的較低優先順序 (>i) 分割作業,即使在先前迭代期間忽略這些作業也一樣。 - 以作業為依據的優先順序。我們會根據作業類型傳播分割作業。「傳遞」作業 (例如元素作業和重塑) 的優先順序最高,而形狀轉換作業 (例如 dot 和 reduce) 的優先順序較低。
- 積極傳播。使用積極策略來傳播分割作業。基本策略只會傳播沒有衝突的切割,而積極策略則會解決衝突。更積極的做法雖然可以減少記憶體占用空間,但可能會影響潛在的通訊。
- 基本傳播方式。這是階層中最低層級的傳播策略,不會進行任何衝突解決,而是在所有運算元與結果之間傳播相容的軸。

這個階層可解讀為巢狀的 for 迴圈。例如,針對每個使用者優先順序,會套用完整的作業優先順序傳播。
作業分割規則
分割規則會引入每個運算的抽象概念,為實際傳播演算法提供所需資訊,以便從運算元傳播分割作業至結果,或跨運算元傳播,而無須考量特定運算類型及其屬性。這項操作本質上是將特定操作的邏輯分離,並為所有操作提供共用表示法 (資料結構),僅供傳播用途。在最簡單的形式中,它只提供以下函式:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
這項規則可讓我們以基於此資料結構 (OpShardingRule) 的一般方式編寫傳播演算法,而非在許多作業中複製類似的程式碼片段,大幅降低作業中發生錯誤或行為不一致的可能性。
讓我們回到 matmul 範例。
將在傳播期間所需的資訊 (也就是維度之間的關係) 封裝在編碼中,可以使用 einsum 符號的形式編寫:
(i, k), (k, j) -> (i, j)
在這個編碼中,每個維度都會對應至單一因素。
傳播如何使用此對應:如果運算元/結果的維度沿著軸分割,傳播作業會在這個對應中查詢該維度的因數,並以相同因數沿著各自的維度分割其他運算元/結果,並且 (依據先前討論的複製作業) 可能也會沿著該軸複製其他沒有該因數的運算元/結果。
複合因子:擴充重塑規則
在許多運算中 (例如 matmul),我們只需要將每個維度對應至單一因數。不過,這對重塑而言是不夠的。
以下重塑作業會將兩個維度合併為一個:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
在此情況下,輸入內容的維度 0 和 1 都對應至輸出內容的維度 0。假設我們先為輸入內容提供因數:
(i,j,k) : i=2, j=4, k=32
您可以看到,如果我們想在輸出內容中使用相同的因素,就需要單一維度來參照多個因素:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
如果重塑是用來分割維度,也可以執行相同的操作:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
請注意,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
這裡的 8 大小維度基本上由 2 和 4 因數組成,因此我們將這些因數稱為 (i,j,k) 因數。
這些因素也適用於沒有任何完整維度對應至其中一個因素的情況:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
這個範例也強調為何我們需要儲存因數大小,因為我們無法輕易從對應的尺寸推斷出這些值。
核心傳播演算法
沿著因數傳播分割
Shardy 中包含張量、維度和因子的階層。代表不同層級的資料。因子是子維度。這是用於區塊傳播作業的內部階層。每個維度可能對應一或多個因素。維度和因子之間的對應是由 OpShardingRule 定義。

Shardy 會沿著因數 (而非維度) 傳播區塊切割軸。如要執行這項操作,我們有三個步驟,如下圖所示:
DimSharding專案至FactorSharding- 在
FactorSharding的空間中散發區塊處理軸 - 投射更新後的
FactorSharding,以取得更新後的DimSharding
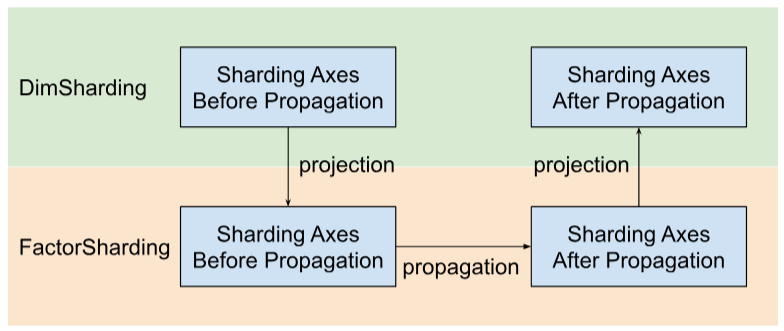
以圖表呈現沿著因素傳播的分割區
我們將使用下表來呈現分割區傳播問題和演算法。
| F0 | F1 | F2 | 明確複製的軸 | |
|---|---|---|---|---|
| T0 | ||||
| T1 | ||||
| T2 |
- 每個欄代表一個因素。F0 代表索引為 0 的因子。我們會沿著因數 (欄) 傳播分割作業。
- 每列代表一個張量。T0 是索引為 0 的張量。張量是特定運算涉及的所有運算元和結果。資料列中的軸不得重疊。一個軸 (或子軸) 無法用於多次分割單一張張量。如果明確複製軸,我們就無法使用該軸分割張量。
因此,每個儲存格都代表一個因數分割。部分張量中可能會缺少因子。C = dot(A, B) 的資料表如下所示。含有 N 的儲存格表示因數不在張量中。例如,F2 位於 T1 和 T2,但不在 T0 中。
C = dot(A, B) |
F0 批次處理暗淡 | F1 非契約式維度 | F2 非收縮型區間 | F3 合約 dim | 明確複製的軸 |
|---|---|---|---|---|---|
| T0 = A | 否 | ||||
| T1 = B | 否 | ||||
| T2 = C | 否 |
收集及傳播區塊劃分軸
我們會使用下列簡單的範例,以視覺化方式呈現傳播情形。
| F0 | F1 | F2 | 明確複製的軸 | |
|---|---|---|---|---|
| T0 | 「a」 | 「f」 | ||
| T1 | 「a」和「b」 | 「c」和「d」 | 「g」 | |
| T2 | 「c」和「e」 |
步驟 1:找出沿著每個因素傳播的軸 (又稱為 (最長) 相容的主要區隔軸)。在本例中,我們會沿著 F0 傳播 ["a", "b"]、沿著 F1 傳播 ["c"],並沿著 F2 傳播空值。
步驟 2:展開因子切割,即可取得下列結果。
| F0 | F1 | F2 | 明確複製的軸 | |
|---|---|---|---|---|
| T0 | 「a」, "b" | "c" | 「f」 | |
| T1 | 「a」和「b」 | 「c」和「d」 | 「g」 | |
| T2 | "a", "b" | 「c」和「e」 |
資料流作業
上述傳播步驟說明適用於大多數作業。不過,在某些情況下,分割規則可能不適用。在這些情況下,Shardy 會定義資料流作業。
某個 op X 的資料流邊緣會在一系列來源和一系列目標之間定義橋接,以便所有來源和目標都以相同方式分割。這類作業的例子包括 stablehlo::OptimizationBarrierOp、stablehlo::WhileOp、stablehlo::CaseOp 和 sdy::ManualComputationOp。最終,任何實作 ShardableDataFlowOpInterface 的作業都會視為資料流作業。
一個運算可擁有多個彼此垂直的資料流邊緣。例如:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
這個 while 運算子有 n 資料流動邊緣:第 i 個資料流動邊緣位於來源 x_i、return_value_i 和目標 y_i、pred_arg_i、body_arg_i 之間。
Shardy 會在資料流程邊緣的所有來源和目標之間傳播分割作業,就好像是使用來源做為運算元,目標做為結果,以及身分 sdy.op_sharding_rule 的一般運算一樣。也就是說,正向傳播是從來源傳播到目標,而反向傳播則是從目標傳播到來源。
使用者必須實作多種方法,說明如何透過擁有者取得每個資料流邊緣的來源和目標,以及如何取得及設定邊緣擁有者的分割區。擁有者是 Shardy 傳播機制所使用的資料流邊緣的使用者指定目標。使用者可以任意選擇,但必須是靜態值。
舉例來說,假設 custom_op 的定義如下:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
這個 custom_op 有兩種資料流邊緣類型:return_value_i (來源) 和 y_i (目標) 之間的 n 邊緣,以及 x_i (來源) 和 body_arg_i (目標) 之間的 n 邊緣。在這種情況下,邊緣擁有者與目標相同。
