タイル表示レイアウト

図 1

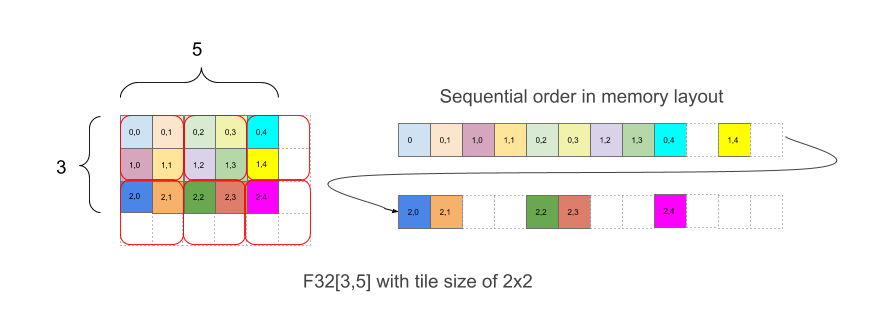
図 1 は、配列 F32[3,5] が 2x2 のタイリングでメモリにレイアウトされる方法を示しています。このレイアウトのシェイプは F32[3,5]{1,0:T(2,2)} として記述されます。1,0 は寸法の物理的な順序（レイアウトの minor_to_major フィールド）、コロンの後の (2,2) は、2x2 タイルによる物理寸法のタイル状を示します。

直感的には、形状を覆うようにタイルが配置され、上の例のように各タイル内に要素がタイルなしでレイアウトされます。この例の右側は、メモリ内のレイアウトを示しています。元の配列境界が平らでない場合でも、完全な 2x2 タイルになるように追加される白いパディング要素が含まれています。

パディング内の追加要素に特定の値を含める必要はありません。

形状とタイルを指定してタイリングするための線形インデックスの式

タイリングなしの場合、配列境界 d=(d_n, d_n-1, ... , d₁)（d1 は最も小さい次元）を持つ配列内の要素 e=(e_n, e_n-1, ... , e₁) は、位置にメジャーからマイナーの順に配置されます。

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + e_n-1

このドキュメントでは、表記をわかりやすくするために、タイルの次元数が配列と同じであると仮定しています。XLA のタイリングの実装では、これは、最初の最大のディメンションを変更せずにタイリングを最もマイナーなディメンションのみに適用することで、ディメンションの少ないタイリングに一般化されます。これにより、指定されたタイリングに、タイルされるシェイプの物理ディメンションの接尾辞が付加されます。

サイズ（t_n、t_n-1、...、t₁）のタイリングを使用すると、インデックス（e_n、e_n-1、...、e₁）を持つ配列内の要素が、最終的なレイアウトの次の位置にマッピングされます。

linear_index_with_tile(e, d, t) _{n - 1, n - 1, n - 1, n - 1, n - 1 - 1 - 1 / n 1 - 1 n 1 / t 1 n 1 - 1 n 1 / t 1 n 1 - 1 t 1 / t 1nnnnnnnnn}

レイアウトは、次の 2 つの部分を持つと考えることができます。(⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋)。これは、サイズのタイルの配列の Tile インデックスに対応します: (Ұd_n/t_n, ... , Ұd₁/t₁ に対応)ceil 関数は 📊?d_i/t_i の形で現れます。なぜなら、タイルがより大きな配列の境界を越えると、図 1 のようにパディングが挿入されるからです。タイルとタイル内の要素はどちらも、タイリングなしで再帰的に配置されます。

図 1 の例では、要素 (2,3) にはタイル インデックス (1,1) と、結合された座標ベクトル (1,1,0,1) のタイル内インデックス (0,1) があります。タイル インデックスの境界は (2,3) で、タイル自体は (2,3,2,2) の結合ベクトルに対して (2,2) です。論理シェイプでインデックス（2,3）を持つ要素のタイルの線形インデックスは次のようになります。

linear_index_with_tile((2,3), (3,5), (2,2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index((1,1), (2,3)) ∙ 2 ∙ 2 + linear_index((0,1) + 1 ∙ 2 = 1)、(2,2)

pad-reshape-transpose としてのタイリング

タイリングベースのレイアウトは次のように動作します。
ディメンションの配列（d_n、d_n-1、...、d1）（d1 は最もマイナーなディメンション）について考えてみましょう。サイズ（t_n、t_n-1、...、t₁）（t₁ が最小の寸法）のタイリングでレイアウトされている場合、そのタイリングは、次のようにパッドの形状変更と転置の観点から説明できます。

1. 配列は、（approvedd_n/t_ntroubleshooting∙t_n, ... , 📊?d₁/t₁Э∙t₁）にパディングされています。
2. 各次元 i は (SELECTEDd_i/ti↘, t_i) のように分割されます。つまり、配列は
   (Ұd_n/t_nᐧ, t_n, ... , タイプ:d₁/t₁Ұ, t₁) に再形成されます。
   この形状変更自体には物理的なレイアウト変更がないため、この形状変更時はビットキャストです。タイルについて明示的に考えていない場合、この形状変更により、パディングされたシェイプと同じ数の要素を持つ任意のシェイプを表現できます。この例は、この方法でタイルを表現する方法を示しています。
3. 転置は、t_n、...、t₁ を、相対的な順序を保ちながら最も小さいディメンションに移動すると、
   になります（Эd_n/t_n↘, ... 、 Цd₁/t₁、t_n、...、t_1）。

最終的な形状には接頭辞
（CameraXd_n/t_n↘, ... , Ұd₁/t₁↘）が付きます。これは、各ディメンション内のタイルの数を表します。配列内の要素（e_n, ... , e₁）は、最終的なシェイプで次の要素にマッピングされます。
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁)。要素の線形インデックスが期待どおり上記の式に従うことは簡単に確認できます。

反復タイル

XLA のタイリングは、繰り返し適用することで、さらに柔軟になります。

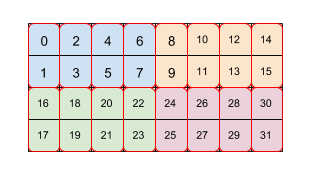
図 2

図 2 は、サイズ 4x8 の配列が 2 つのレベルのタイリング（最初の 2x4、次に 2x1）でタイルされる様子を示しています。この繰り返しのタイリングを (2,4)(2,1) と表現します。それぞれの色は 2x4 のタイルを表し、赤い枠線ボックスは 2x1 のタイルを表します。数値は、タイル形式のその要素のメモリ内の線形インデックスを示します。この形式は、TPU の BF16 に使用される形式と一致しますが、初期タイルの方が大きい、つまり（8,128）（2,1）のタイリングです。2 x 1 で 2 つ目のタイリングの目的は、TPU のアーキテクチャに合わせて 2 つの 16 ビット値を収集して 1 つの 32 ビット値を形成することです。

2 番目以降のタイルは、この例の (8,128)(2,1) のようにタイル内のデータを再配置するだけのマイナー タイル内ディメンションの両方を参照できますが、前のタイルの主要なクロスタイル ディメンションを参照することもできます。

タイルを使用してディメンションを組み合わせる

XLA のタイリングでは、ディメンションの結合もサポートされています。たとえば、F32[2,7,8,11,10]{4,3,2,1,0} のディメンションを F32[112,110]{1,0} に結合してから、(2,3) と並べることができます。使用されるタイルは (∗,∗,2,∗,3) です。ここでのタイルのアスタリスクは、そのディメンションを取得し、次のマイナー ディメンションと組み合わせることを意味します。隣接する複数のディメンションを 1 つのディメンションにまとめることができます。包含ディメンションは、タイルのそのディメンションのタイル値 -1 で表されます。それ以外の場合、ディメンション サイズとしてタイルで有効になりません。

正確には、シェイプのディメンション i がタイルのアスタリスクによって除去されている場合、以前のタイリングの定義が適用される前に、そのディメンションはタイルされるシェイプとタイル ベクトルの両方から削除され、シェイプの次元 i-1 の配列境界は d_i-1 から d_id_i-1 に増加します。この手順は、タイルベクトルのアスタリスクごとに繰り返されます。