Diseño de mosaico

Figura 1

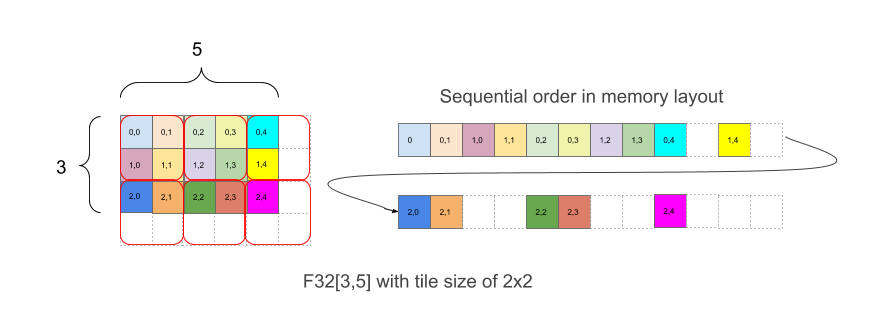
La Figura 1 muestra cómo un array F32[3,5] se distribuye en la memoria con mosaicos de 2x2. Una forma con este diseño se escribe como F32[3,5]{1,0:T(2,2)}, donde 1,0 se relaciona con el orden físico de las dimensiones (campo minor_to_major en el diseño), mientras que (2,2) después de los dos puntos indica la distribución de las dimensiones físicas con un mosaico de 2 × 2.

De manera intuitiva, las tarjetas se disponen para cubrir la forma y, dentro de cada tarjeta, se disponen los elementos sin mosaicos, como en el ejemplo anterior, donde la parte derecha del ejemplo muestra el diseño en la memoria, incluidos los elementos de padding blanco que se agregan para tener mosaicos completos de 2 x 2, aunque los límites originales del array no sean uniformes.

No es necesario que los elementos adicionales en el padding contengan ningún valor en particular.

Fórmulas de índice lineal para mosaicos a partir de una forma y un mosaico

Sin mosaicos, un elemento e=(e_n, e_n-1, ... , e₁) en un array con límites de array d=(d_n, d_n-1, ... , d₁) (d1 es la dimensión más secundaria) se dispone de mayor a menor en la posición:

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1... d₁ +_n-1... +_n-1

Para simplificar la notación en este documento, suponemos que una tarjeta tiene la misma cantidad de dimensiones que el array. En la implementación de mosaicos de XLA, esto se generaliza para crear mosaicos con menos dimensiones. Para ello, se dejan las dimensiones iniciales más importantes sin modificar y se aplican únicamente en las más pequeñas, de modo que la tarjeta que se especifica mencione un sufijo de las dimensiones físicas de la forma que se está mostrando.

Cuando se usan mosaicos de tamaño (t_n, t_n-1, ... , t₁), un elemento del array con índices (e_n, e_n-1, ..., e₁) se asigna a esta posición en el diseño final:

_n

Se puede considerar que el diseño tiene dos partes: (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋), que corresponde a un índice de mosaicos en un array de mosaicos de tamaño (⌈d_{n/tn⌉, ... , ⌈d}⌉ La función ceil aparece en ⌈d_i/t_i⌉ porque si los mosaicos superan los límites del array más grande, el padding se inserta como en la Figura 1. Tanto las tarjetas como los elementos dentro de las tarjetas se disponen de forma recursiva sin mosaicos.

Para el ejemplo de la Figura 1, el elemento (2,3) tiene un índice de mosaico (1,1) y un índice dentro del mosaico (0,1) para un vector de coordenadas combinado de (1,1,0,1). Los índices de tarjetas tienen límites (2,3) y la propia tarjeta es (2,2) para un vector combinado de (2,3,2,2). Entonces, se procesa el índice lineal con mosaico del elemento con índice (2,3) en la forma lógica.

linear_index_with_tile((2,3), (3,5), (2,2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index(1,1), (2,3)) ∙ 2 ∙ 2 + lineal_index((0,1)

Mosaico como pad-reshape-transpose

El diseño basado en mosaicos funciona de la siguiente manera:
Considera un array de dimensiones (d_n, d_n-1, ... , d1) (d1 es la dimensión más secundaria). Cuando se presenta con mosaicos de tamaño (t_n, t_n-1, ... , t₁) (t₁ es la dimensión más pequeña), esa representación se puede describir en términos de pad-reforma-transposición de la siguiente manera.

1. El array se rellena a (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁).
2. Cada dimensión i se divide en (⌈d_i/ti⌉, t_i), es decir, el array cambia de forma a
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁).
   No hay ningún cambio de diseño físico en esta reforma por sí sola, por lo que se trata de una predicción de bits. Si no se piensa explícitamente en una tarjeta, este cambio de forma podría expresar cualquier forma con la misma cantidad de elementos que la forma con padding. El ejemplo aquí es cómo expresar una tarjeta de esta manera.
3. Una transposición se produce moviendo t_n, ... , t₁ a las dimensiones más secundarias mientras se mantiene su orden relativo, de modo que el orden de las dimensiones de la mayor a la más secundaria pasa a ser
   (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉, t_n).

La forma final tiene el prefijo
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉), que describe la cantidad de mosaicos de cada dimensión. Un elemento del array (e_n, ... , e₁) se asigna a este elemento en la forma final:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , mod1)._{1 Es fácil ver que el índice lineal del elemento sigue la fórmula anterior, como se esperaba.}

Mosaicos repetidos

Los mosaicos de XLA se vuelven aún más flexibles si se aplican repetidamente.

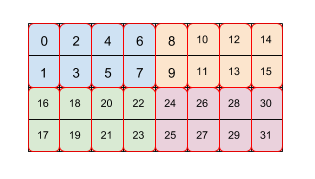
Figura 2

En la Figura 2, se muestra cómo un array de tamaño 4 × 8 está representado en mosaico por dos niveles de mosaicos (primero 2 × 4 y, luego, 2 × 1). Representamos este mosaico repetido como (2,4)(2,1). Cada color indica una tarjeta de 2 × 4 y cada cuadro de borde rojo es un mosaico de 2 × 1. Los números indican el índice lineal en la memoria de ese elemento en el formato en mosaico. Este formato coincide con el formato usado para BF16 en la TPU, con la excepción de que la tarjeta inicial es más grande, es decir, la mosaico es (8,128)(2,1), donde el propósito de la segunda representación en mosaico de 2x1 es recopilar dos valores de 16 bits para formar un valor de 32 bits de forma que se alinee con la arquitectura de una TPU.

Ten en cuenta que una segunda tarjeta o una posterior puede hacer referencia a las dimensiones menores dentro de la tarjeta, que solo reorganizan los datos dentro de ella, como en este ejemplo con (8,128)(2,1), pero también puede hacer referencia a las dimensiones principales de tarjetas cruzadas de la tarjeta anterior.

Cómo combinar dimensiones mediante mosaicos

La mosaicos de XLA también admite la combinación de dimensiones. Por ejemplo, puede combinar las dimensiones de F32[2,7,8,11,10]{4,3,2,1,0} en F32[112,110]{1,0} antes de usarla en mosaico con (2,3). El mosaico utilizado es (∗,∗,2,∗,3). En este caso, un asterisco en una tarjeta implica tomar esa dimensión y combinarla con la siguiente dimensión más secundaria. Se pueden sumar varias dimensiones adyacentes en una sola dimensión. Una dimensión reducida se representa con un valor de -1 en esa dimensión, que, de lo contrario, no es válida en una tarjeta como tamaño de dimensión.

Más precisamente, si se elimina la dimensión i de la forma mediante un asterisco en la tarjeta, antes de que se aplique la definición anterior de mosaico, esa dimensión se quita tanto de la forma en mosaico como del vector de mosaico, y lo que fue una dimensión i-1 de la forma aumentará su límite de array de d_i-1 a d_id_i-1. Este paso se repite para cada asterisco en el vector de mosaicos.