टाइल वाला लेआउट

पहली इमेज

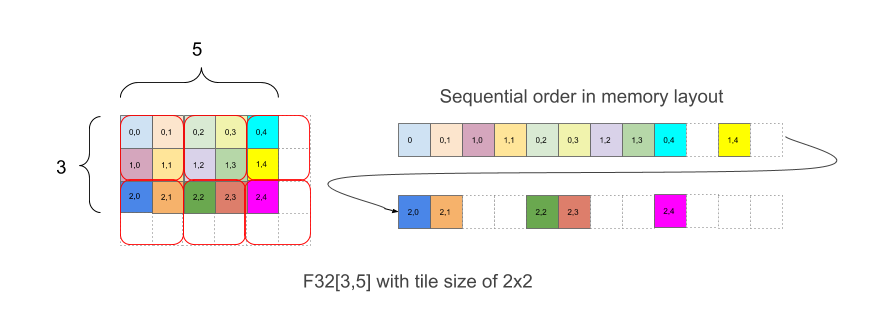
पहली इमेज में दिखाया गया है कि 2x2 टाइलिंग के साथ, मेमोरी में F32[3,5] अरै को कैसे रखा जाता है. इस लेआउट का एक आकार F32[3,5]{1,0:T(2,2)} के रूप में लिखा गया है, जिसमें 1,0 डाइमेंशन के फ़िज़िकल ऑर्डर से जुड़ा है (लेआउट में minor_to_major फ़ील्ड) और (2,2) कोलन के बाद 2x2 टाइल से फ़िज़िकल डाइमेंशन की टाइलिंग की जानकारी मिलती है.

आकार को ढंकने के बाद हर टाइल में टाइलें बिछाई जाती हैं, फिर एलिमेंट बिना टाइल के बिछाए जाते हैं, जैसा कि ऊपर दिए गए उदाहरण में किया गया है, जहां उदाहरण के दाएं हिस्से में लेआउट, मेमोरी में दिखता है. इसमें सफ़ेद पैडिंग एलिमेंट शामिल हैं, जिन्हें 2x2 टाइल को पूरा करने के लिए जोड़ा जाता है, भले ही मूल अरे की सीमाएं समान न हों.

पैडिंग में मौजूद अतिरिक्त एलिमेंट में कोई खास वैल्यू शामिल करना ज़रूरी नहीं है.

आकार और टाइल के आधार पर टाइल लगाने के लिए, लीनियर इंडेक्स फ़ॉर्मूला

टाइलिंग के बिना, d=(d_n, d_n-1, ... , d₁) (d1 सबसे छोटा डाइमेंशन) कैटगरी में मौजूद अरे में, एलिमेंट e=(e_n, e_n-1, ... , e₁) को उस पोज़िशन पर मेजर से लेकर माइनर ऑर्डर तक तय किया जाता है:

Linear_index(e, d)
= Linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ +_{dn-1 +d-1}

इस दस्तावेज़ में नोटेशन की आसानी के लिए, हम यह मान लेते हैं कि टाइल में उतने ही डाइमेंशन हैं जितने अरे हैं. एक्सएलए में टाइलिंग को लागू करने में, इसे सामान्य तौर पर कम डाइमेंशन वाली टाइलिंग के लिए इस्तेमाल किया जाता है. ऐसा करने के लिए, सबसे मुख्य डाइमेंशन में कोई बदलाव नहीं किया जाता है. साथ ही, सबसे माइनर डाइमेंशन पर टाइल लागू की जाती हैं, ताकि बताई गई टाइल, टाइल किए जा रहे आकार के फ़िज़िकल डाइमेंशन का सफ़िक्स बना सके.

जब साइज़ (t _n, t_n-1, ... , t₁) का इस्तेमाल किया जाता है, तो इंडेक्स (e_n, e_n-1, ... , e₁) वाली कलेक्शन में मौजूद किसी एलिमेंट को फ़ाइनल लेआउट में इस पोज़िशन पर मैप किया जाता है:

LINEar_index_with_ile(e, d, n ∌ रहता_टाइल(e, d, ⋌⌋1) n- दोबारा,_{emod फ़ॉर्मैट, फ़ॉर्मैट फ़ॉर्मैट, ियन ⌋ दोबारा,
= Linear_index(⌊e/t⌋, e mod t), (⌈d/t⌉, t)) (अरिथमेटिक इसका एलिमेंट एलिमेंट वाइस, (a,b) है स्ट्रिंगn}

लेआउट के दो हिस्सों को समझा जा सकता है: (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋), जो साइज़ की कलेक्शन वाली कैटगरी के टाइल इंडेक्स के मुताबिक होते हैं (⌈d_n/t_nमोद_nऔर ... , /_{t1 ⌋, ... , ⌊e1/t1⌋), इंडेक्स n/tnविकेड nss सील फ़ंक्शन इस तरह का दिखता है ⌈di/ti⌉ क्योंकि अगर टाइल बड़ी रेंज की सीमाओं को पार कर जाती हैं, तो पैडिंग (जगह) को पहली इमेज में शामिल किया जाता है. टाइल के अंदर की टाइल और एलिमेंट, दोनों को टाइल किए बिना बार-बार बनाया जाता है.}

इमेज 1 के उदाहरण के लिए, (1,1,0,1) के कंबाइंड कोऑर्डिनेट वेक्टर के लिए, एलिमेंट (2,3) में टाइल इंडेक्स (1,1) और इन-टाइल इंडेक्स (0,1) है. टाइल इंडेक्स में (2,3,2,2) के कंबाइंड वेक्टर के लिए बाउंड (2,3) और टाइल (2,2) हैं. लॉजिकल आकार में इंडेक्स (2,3) वाले एलिमेंट के लिए टाइल वाला लीनियर इंडेक्स फिर होगा

PUBLISHER linear_index_with_till((2,3), (3,5), (2,2))
= Linear_index((1,1,0,1), (2,3,2,2))
= लीनियर_इंडेक्स(1,1), (2,3)) 2 2 + लीनियर_इंडेक्स ((0,1) ) (2, 2),

पैड के आकार को ट्रांसपोज़ करने की तरह टाइलिंग

टाइल पर आधारित लेआउट इस तरह काम करता है:
डाइमेंशन की रेंज चुनें (d_n, d_n-1, ... , d1) (d1 सबसे छोटा डाइमेंशन है). जब यह साइज़ (t_n, t_n-1, ... , t₁) (t₁ सबसे छोटा डाइमेंशन होता है) की टाइलिंग के साथ बनाया जाता है, तो उस टाइलिंग के बारे में पैड के आकार में बदलाव करके, इस तरीके से बताया जा सकता है.

1. अरे को (⌈d_n/t_n⌉t_n, ... , ⌈d₁/t₁⌉換t₁) में जोड़ा जाता है.
2. हर डाइमेंशन i को (⌈d_i/ti⌉, t_i) में बांटा जाता है, यानी अरे को बदलकर
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁) किया जाता है.
   इस बदलाव में, इनके लेआउट में अपने-आप कोई बदलाव नहीं होता है. इसलिए, यह बदलाव एक बिटकास्ट होता है. अगर किसी टाइलिंग के बारे में साफ़ तौर पर नहीं बताया जा रहा है, तो यह बदलाव किसी भी आकार को उतने ही एलिमेंट के साथ दिखा सकता है जितने पैड किए गए आकार में किया गया है - उदाहरण में, टाइल को इस तरह से दिखाने का तरीका बताया गया है.
3. ट्रांसपोज़ करने के लिए, t_n, ... , t₁ को सबसे नाबालिक डाइमेंशन पर ले जाकर, सबसे छोटा डाइमेंशन तय किया जाता है. इससे सबसे ज़्यादा डाइमेंशन से लेकर सबसे माइनर तक के डाइमेंशन का क्रम
   (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌈, ... t_{) हो जाता है.}

आखिरी आकार में
प्रीफ़िक्स
होता है (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉), जो हर डाइमेंशन में टाइल की संख्या के बारे में बताता है. अरे में किसी एलिमेंट (e_n, ... , e₁) को इस एलिमेंट के साथ फ़ाइनल आकार में मैप किया जाता है:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁). यह देखना आसान है कि एलिमेंट का लीनियर इंडेक्स, ऊपर दिए गए फ़ॉर्मूला के हिसाब से काम करता है.

बार-बार टाइल लगाने की सुविधा

एक्सएलए की टाइलिंग, बार-बार लागू करने से और भी ज़्यादा सुविधाजनक हो जाती है.

दूसरी इमेज

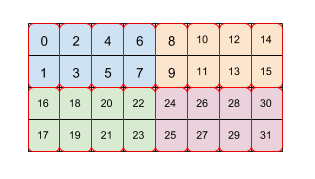
दूसरी इमेज में दिखाया गया है कि 4x8 साइज़ के अरे को टाइलिंग के दो लेवल (पहले 2x4 फिर 2x1) से कैसे टाइल किया जाता है. हम दोहराए गए इस टाइलिंग को (2,4)(2,1) के तौर पर दिखाते हैं. हर रंग 2x4 टाइल का संकेत देता है और हर लाल बॉर्डर बॉक्स 2x1 टाइल के तौर पर होता है. ये नंबर, टाइल वाले फ़ॉर्मैट में उस एलिमेंट की मेमोरी में मौजूद लीनियर इंडेक्स को दिखाते हैं. यह फ़ॉर्मैट, TPU पर BF16 के लिए इस्तेमाल किए गए फ़ॉर्मैट से मेल खाता है. हालांकि, इसकी शुरुआती टाइल बड़ी है (8,128) (2,1). इसमें टाइलिंग (8,128)(2,1) है, जहां 2x1 की मदद से दूसरी टाइलिंग का मकसद 32-बिट की दो वैल्यू को इस तरह इकट्ठा करना है कि वह TPU के आर्किटेक्चर के मुताबिक हो.

ध्यान दें कि दूसरी या बाद वाली टाइल, माइनर इन-टाइल डाइमेंशन का हवाला दे सकती है, जो टाइल के अंदर सिर्फ़ डेटा को फिर से व्यवस्थित करता है, जैसा कि इस उदाहरण में (8,128)(2,1) के साथ किया गया है. हालांकि, यह पहले वाली टाइल के मुख्य क्रॉस-टाइल डाइमेंशन का भी हवाला दे सकता है.

टाइल का इस्तेमाल करके डाइमेंशन जोड़ना

एक्सएलए की टाइलिंग, डाइमेंशन को भी मिलाने की सुविधा के साथ काम करती है. उदाहरण के लिए, यह F32[2,7,8,11,10]{4,3,2,1,0} में मौजूद डाइमेंशन को F32[112,110]{1,0} में जोड़कर (2,3) पर टाइल कर सकता है. इस टाइल का इस्तेमाल किया गया है (∗,∗,2,∗,3). यहां टाइल में तारे के निशान का मतलब है उस डाइमेंशन को लेकर उसे अगले छोटे डाइमेंशन के साथ जोड़ना. पास-पास मौजूद कई डाइमेंशन को एक डाइमेंशन में शामिल किया जा सकता है. टाइल के उस डाइमेंशन में शामिल डाइमेंशन को टाइल की वैल्यू -1 से दिखाया जाता है, जो किसी टाइल में डाइमेंशन साइज़ के तौर पर मान्य नहीं है.

ज़्यादा सटीक तौर पर, अगर टाइल में से तारे के निशान के ज़रिए आकार i को हटाया जाता है, तो टाइलिंग की पिछली परिभाषा लागू करने से पहले, वह डाइमेंशन टाइल किए जा रहे आकार और टाइल वेक्टर, दोनों से हटा दिया जाता है और आकार के डाइमेंशन i-1 की अरे की सीमा d_i-1 से d_id_i-1 तक बढ़ जाती है. टाइल वेक्टर में मौजूद हर तारे के निशान के लिए, यह चरण दोहराया जाता है.