타일 레이아웃

그림 1

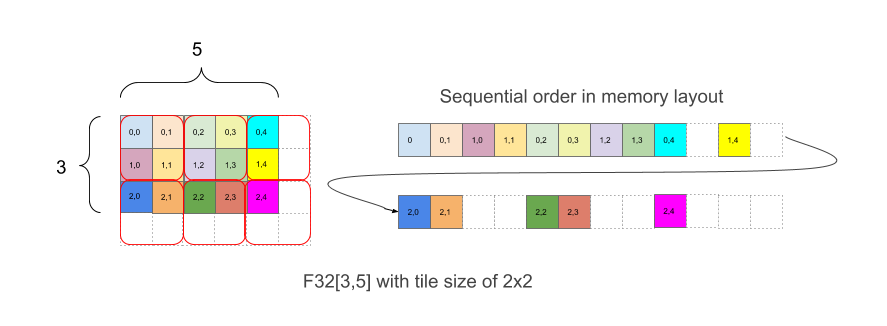
그림 1은 배열 F32[3,5] 가 2x2 타일로 메모리에 배치되는 방식을 보여줍니다. 이 레이아웃의 도형은 F32[3,5]{1,0:T(2,2)}로 작성됩니다. 여기서 1,0은 차원의 물리적 순서 (레이아웃의 minor_to_major 필드)와 관련이 있는 반면 콜론 뒤의 (2,2)는 2x2 타일의 실제 크기 타일링을 나타냅니다.

직관적으로 타일은 도형을 덮도록 배치된 다음 각 타일 내에 타일 없이 배치됩니다. 위의 예에서와 같이 예의 오른쪽 부분에는 메모리의 레이아웃이 표시됩니다. 여기에는 원래 배열 경계가 짝수가 아니더라도 2x2 타일을 완성하기 위해 추가된 흰색 패딩 요소가 포함됩니다.

패딩의 추가 요소는 특정 값을 포함할 필요가 없습니다.

주어진 도형과 타일에 대한 타일 지정을 위한 선형 색인 수식

타일링을 사용하지 않으면 배열 경계가 d=(d_n, d_n-1, ... , d₁)인 배열의 요소 e=(e_n, e_n-1, ... , e₁) (d1이 가장 작은 차원임)이 위치에서 큰 순서로 표시됩니다.

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + _{n-1...d1 +n-2 ...}

이 문서에서는 편의를 위해 타일의 차원 수가 배열과 동일하다고 가정합니다. XLA의 타일 구현에서는 초기의 가장 큰 치수를 변경하지 않고 타일은 가장 작은 치수에만 적용하여 더 적은 크기의 타일로 일반화됩니다. 따라서 지정된 타일은 타일링되는 도형의 실제 치수의 접미사를 언급합니다.

크기 타일링 (t_n, t_n-1, ... , t₁)을 사용하면 색인이 있는 배열의 요소 (e_n, e_n-1, ... , e₁)가 최종 레이아웃에서 다음 위치에 매핑됩니다.

을


_n

레이아웃은 _{(⌊en/tn⌋, ... , ⌊e1/t1⌋) 두 부분으로 구성되며, 이는 a} ceil 함수는 ⌈d_i/t_i⌉에 표시됩니다. 타일이 더 큰 배열의 경계를 초과하면 그림 1과 같이 패딩이 삽입되기 때문입니다. 카드 내의 카드와 요소는 모두 타일 없이 재귀적으로 배치됩니다.

그림 1의 예에서 요소 (2,3)에는 (1,1,0,1)의 결합된 좌표 벡터를 나타내는 타일 색인 (1,1)과 타일 내 색인 (0,1)이 있습니다. 카드 색인에는 경계 (2,3)가 있고 카드 자체는 (2,3,2,2)의 결합된 벡터의 경우 (2,2)입니다. 그러면 논리 도형에서 색인 (2,3)이 있는 요소의 타일이 있는 선형 색인은 다음과 같습니다.

linear_index_with_tile((2,3), (3,5), (2,2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index((1,1), (2,3)) ∙ 2 2 ∙ 2 + linear_index((0,1) ∙ 2 ∙ (1, 1) ∙
∙ (2, 1) ∙ (2, 2)

패드-형태-트랜스포즈로 타일링

타일 기반 레이아웃은 다음과 같이 작동합니다.
차원 배열 (d_n, d_n-1, ... , d1)을 고려합니다(d1이 가장 작은 차원임). 타일이 크기(t_n, t_n-1, ... , t₁) (t₁이 최하위 차원임)의 타일로 배치되면 다음과 같이 패드의 형태 변경-전치에 관해 설명할 수 있습니다.

1. 배열은 (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁)에 패딩됩니다.
2. 각 차원 i는 (⌈d_i/ti⌉, t_i)로 나뉩니다. 즉, 배열의 형태가
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁)로 변경됩니다.
   이 재구성 자체에는 실제 레이아웃이 변경되지 않으므로 이 재구성은 비트캐스트입니다. 명시적으로 타일을 생각하지 않는 경우 이 재구성에서는 패딩 처리된 도형과 동일한 수의 요소를 가진 도형을 표현할 수 있습니다. 다음 예는 이러한 방식으로 카드를 표현하는 방법을 보여줍니다.
3. 전치는 t_n, ... , t₁을 가장 작은 차원으로 이동하면서 상대적인 순서를 유지하여 가장 장음에서 가장 작은 차원으로 가는 순서를
   가 되도록 합니다. (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉, t _{..., tn)}

최종 도형에는 각 치수의 타일 수를 나타내는
접두사 (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉)가 있습니다. 배열의 요소 (e_n, ... , e₁)는 최종 모양에서 이 요소에 매핑됩니다.
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁). 요소의 선형 색인이 위 수식을 예상대로 따르는 것을 쉽게 확인할 수 있습니다.

반복되는 타일

XLA의 타일은 반복적으로 적용하면 더욱 유연해집니다.

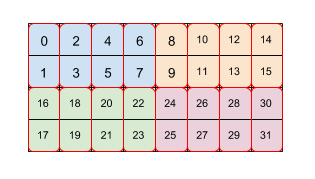
그림 2

그림 2는 4x8 크기의 배열이 2가지 수준의 타일 (처음 2x4, 2x1)으로 어떻게 타일링되는지를 보여줍니다. 이 반복되는 타일식은 (2,4)(2,1)로 표현됩니다. 각 색상은 2x4 타일을 나타내고 각 빨간색 테두리 상자는 2x1 타일입니다. 숫자는 해당 요소의 메모리에 있는 선형 색인을 타일 형식으로 나타냅니다. 이 형식은 TPU의 BF16에 사용된 형식과 일치합니다. 단, 초기 타일이 더 큰 경우, 즉 타일링은 (8,128)(2,1)이며, 여기서 2x1 타일링의 목적은 16비트 값 2개를 함께 수집하여 TPU의 아키텍처와 일치하는 방식으로 1개의 32비트 값을 형성하는 것입니다.

두 번째 이상의 타일은 이 예에서 (8,128)(2,1)와 같이 타일 내에서 데이터를 재정렬하는 보조 타일 크기를 모두 참조할 수 있지만, 이전 타일링의 주요 교차 타일 크기를 참조할 수도 있습니다.

타일을 사용하여 측정기준 결합

XLA의 타일은 치수 결합도 지원합니다. 예를 들어 F32[2,7,8,11,10]{4,3,2,1,0}의 차원을 (2,3)과 타일로 배치하기 전에 먼저 F32[112,110]{1,0}으로 결합할 수 있습니다. 사용된 타일은 (**, 열람,2,참고,3)입니다. 여기서 카드의 별표는 해당 차원을 가져와 다음 보조 차원과 결합하는 것을 의미합니다. 인접한 여러 차원을 하나의 차원으로 함께 포함할 수 있습니다. 포함되는 치수는 타일의 해당 치수에서 -1로 표시되며, 이는 다른 경우 타일에서 치수 크기로 유효하지 않습니다.

더 정확하게는, 타일의 별표를 통해 도형의 차원 i가 제거되면 타일링의 이전 정의가 적용되기 전에 타일로 지정된 도형과 타일 벡터 모두에서 차원이 삭제되며, 도형의 차원 i-1은 배열 경계가 d_i-1에서 d_id_i-1로 증가합니다. 이 단계는 타일 벡터의 각 별표에 대해 반복됩니다.