並排版面配置

圖 1

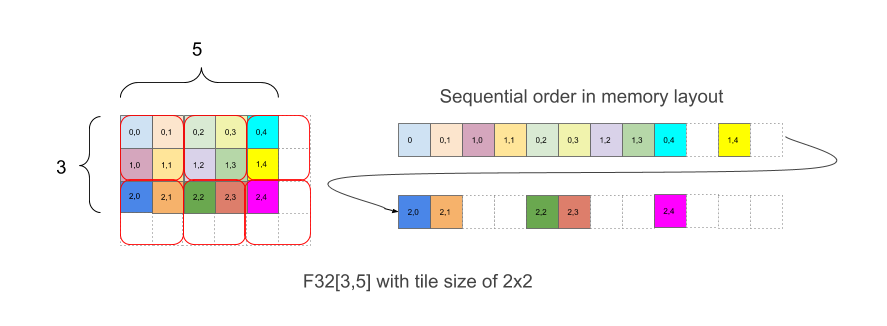
圖 1 顯示陣列 F32[3,5] 如何透過 2x2 圖塊在記憶體中配置。這個版面配置的形狀會以 F32[3,5]{1,0:T(2,2)} 寫成，其中 1,0 與實際維度順序 (Layout 中的 minor_to_major 欄位) 相關，而冒號後 (2,2) 表示實際尺寸的傾斜度為 2x2 圖塊。

直覺上，圖塊會遮住形狀，然後在每個資訊方塊內，元素會在沒有傾斜設定的情況下排出。如上例所示，範例的右側部分在記憶體中顯示版面配置，包括為了達到完整 2x2 圖塊而新增的白色邊框間距元素 (即使原本的陣列邊界並非平均)。

邊框間距中的額外元素不一定要包含任何特定值。

針對特定形狀和圖塊傾斜的線性索引公式

在沒有傾斜設定的情況下，如果陣列中的元素 e=(e_n、e_n-1、...、e₁) 位於陣列範圍 d=(d_n, d_n-1, ... , d₁) 的陣列中，就會被主要維度排放 (d1 是最小的次要順序)：

Linear_index(e, d)
= Linear_index((e_n, e_n-1, ... , e₁)、(d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + d_n-1

為了簡化本文件中的記號，我們假設資訊方塊的維度數量與陣列相同。在 XLA 的圖塊實作中，這樣做一般化為保持維度較少的圖塊，也就是保持初始最主要維度維持不變，並且只將傾斜角度套用至最微維度，這樣指定的傾斜角度就會提及要圖塊的實體維度後置字串。

使用大小的傾斜度 (t_n、t_n-1、... 、 t₁) 時，陣列中的元素 (e_n、e_n-1、...、e₁) 會對應至最終版面配置中的這個位置：

_n

版面配置可分為兩個部分：_nCil 函式會出現在 帳單帳戶 - 全家_i資訊方塊內的資訊方塊和元素都會以遞迴方式顯示，而非並排顯示。

以圖 1 的例子來說，元素 (2,3) 具有圖塊索引 (1,1) 和圖塊內索引 (0,1)，組合的座標向量為 (1,1,0,1)。圖塊索引設有邊界 (2、3)，而圖塊本身為 (2,2) 的合併向量 (2,3,2,2)。含有圖塊的線性索引，在邏輯形狀中為索引 (2,3) 的元素

Linear_index_with_tile((2,3)、(3,5)、(2,2))
= 線性_索引((1,1,0,1), (2,3,2,2))
= 線性_index((1,1), (2,3)) ∙ ·
+ 2 + 線性_index((0,1))

以紙牌換取

傾斜式版面配置的運作方式如下：
請考慮維度陣列 (d_n、d_n-1......、d1) (d1 是最小的維度)。當這包括 _n、t_n-1、... 、t₁) (₁ 是最次要的尺寸) 繪製時，您可以按照以下方式說明立體重新塑形的傾斜角度。

1. 陣列的填充值會增加為 (帳單帳戶)_n
2. 每個維度我都會拆分為 (帳單帳戶) 的 COd_i/ti♦、t_i；也就是說，陣列的重新形狀為
   (總部_n/t_n刻 t_n, ... 的關聯性₁/t₁/t₁)。
   這個重組本身沒有任何實體版面配置變更，因此這個重形是一個位元。如果其中人員未明確想到傾斜角度，此重新形狀可以表示任何與已填充形狀的元素數量相同的任何形狀。這裡的範例是以這種方式表示圖塊。
3. 轉置指的是：將 t_n、... 、t₁ 移至最小尺寸並保留其相對順序，使由最主要到最微小的尺寸排序變為
   (不會影響最主要到最次要的尺寸順序為
   (不會影響)_n/t_n, ... , twd₁/t₁, t_n, 1... ... ... ...

最後一個形狀的前置字元為
(上有大_n/t_n金錢、... , 耳號₁/t₁棋)，說明瞭每個維度中的圖塊數量。陣列中的元素 (e_n、...、e₁) 會對應至最終形狀中的以下元素：
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁)。您可以輕易看到元素的線性索引遵循上述公式。

重複圖塊

XLA 的傾斜角度功能會重複套用，變得更加靈活。

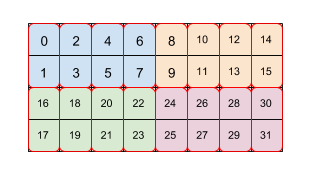
圖 2

圖 2 顯示如何以兩個傾斜層級 (前 2x4 再 2x1) 並排顯示 4x8 大小的陣列。我們所呈現的重複傾斜角度為 (2,4)(2,1)。每個顏色都代表 2x4 的圖塊，每個紅色邊框方塊則為 2x1 的圖塊。這些數字代表圖塊格式記憶體中的線性索引。這種格式符合 TPU 上 BF16 所用的格式，但初始圖塊尺寸較大 (亦即傾斜角度為 (8,128)(2,1)；第二個 2x1 的傾斜度目標則是收集兩個 32 位元值，並依照 TPU 的架構形成一個 32 位元值。

請注意，第二或較晚的資訊方塊可以同時參照圖塊內部維度，這些維度只會重新排列資訊方塊內的資料，如本例使用 (8,128)(2,1) 所示，但也可以參照先前圖塊的主要跨圖塊維度。

使用資訊方塊合併維度

XLA 的傾斜功能也支援合併維度。例如，它可以先將 F32[2,7,8,11,10]{4,3,2,1,0} 中的維度結合為 F32[112,110]{1,0}，然後再傾斜 (2,3)。使用的資訊方塊是 (Ъ、Ъ、2、保留在 3)。資訊方塊中的一個星號意味著要採用該維度，並與下一個更小的維度結合。多個相鄰維度可以合併成一個維度。子總和的維度會以 -1 的圖塊值來表示，在圖塊中對這個維度大小來說就無效。

更精確地說，如果形狀的維度 i 是以圖塊中的星號消除，則在套用圖塊定義之前，該維度都會從圖塊的形狀和圖塊向量中移除，以及形狀的 i-1 維度從 d_i-1 增加到陣列邊界的 _i-1i-1。對於圖塊向量中的每個星號，系統會重複執行這個步驟。