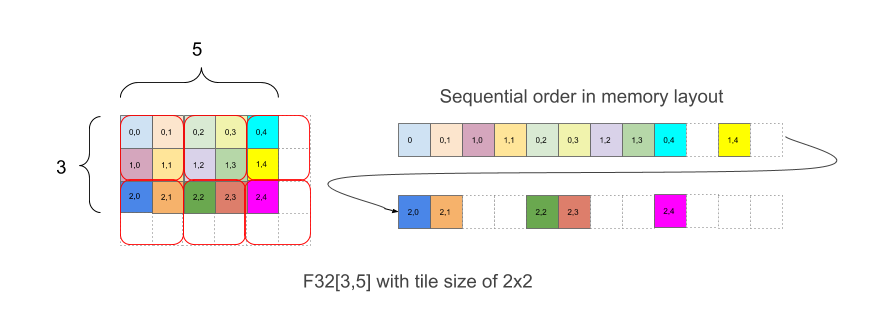
Figura 1
La figura 1 mostra come una matrice F32[3,5] è disposta in memoria con tiling 2x2. Una forma con questo layout è scritta come F32[3,5]{1,0:T(2,2)}, dove 1,0 si riferisce
all'ordine fisico delle dimensioni (campo minor_to_major in Layout), mentre (2,2)
dopo i due punti indica il riquadro delle dimensioni fisiche con un riquadro 2x2.
Intuitivamente, i riquadri vengono disposti per coprire la forma e, all'interno di ogni riquadro, gli elementi vengono poi disposti senza affiancare, come nell'esempio precedente, dove la parte destra dell'esempio mostra il layout in memoria, inclusi gli elementi di spaziatura interna bianca che vengono aggiunti per ottenere riquadri 2 x 2 completi anche se i limiti dell'array originali non sono uniformi.
Gli elementi aggiuntivi nella spaziatura interna non devono contenere alcun valore specifico.
Formule dell'indice lineare per la creazione di riquadri di una forma e di un riquadro
Senza tiling, un elemento e=(en, en-1, ... , e1) in un array con limiti di array d=(dn, dn-1, ... , d1) (d1 è la dimensione minore) viene disposto dall'ordine maggiore a quello minore nella posizione:
indice_lineare(e, d)
= indice_lineare((en, en-1, ... , e1),
(dn, dn-1, ... , d1))
= endn-1...d1 +
en-1...dn-1 +
en-1 ... dn-1
Per semplicità di notazione in questo documento, supponiamo che un riquadro abbia lo stesso numero di dimensioni dell'array. Nell'implementazione dei riquadri di XLA, questo è generalizzato ai riquadri con meno dimensioni, lasciando invariate le dimensioni iniziali più importanti e applicando i riquadri solo alle dimensioni più minori, in modo che il tiling specificato menzioni un suffisso delle dimensioni fisiche della forma a mosaico.
Quando viene utilizzato il tiling di dimensione (tn, tn-1, ... , t1), un elemento dell'array con indici (en, en-1, ..., e1) viene mappato a questa posizione nel layout finale:
<br-ph-1-ph-1<ph-1-ph-1
<br class-1-ph-1<ph-1-ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1-ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<ph-1<br e mod
n
Il layout può essere considerato come costituito da due parti: (⌊en/tn⌋, ... , ⌊e1/t1⌋), che corrisponde a un indice di riquadro in un array di riquadri di dimensioni (⌈dn/tn⌉, ... , nds/1/ La funzione ceil viene visualizzata in ⌈di/ti⌉ perché se i riquadri superano i limiti dell'array più grande, la spaziatura interna viene inserita come nella Figura 1. Sia le tessere che gli elementi al loro interno sono disposti in modo ricorsivo senza piastrelle.
Nell'esempio della Figura 1, l'elemento (2,3) ha indice riquadro (1,1) e indice interno riquadro (0,1), per un vettore di coordinate combinato (1,1,0,1). Gli indici dei riquadri hanno limiti (2,3) e il riquadro stesso è (2,2) per un vettore combinato di (2,3,2,2). L'indice lineare con riquadro per l'elemento con indice (2,3) nella forma logica viene quindi
Riquadrizzazione come pad-rimodellazione-trasposizione
Il layout basato su riquadri funziona come segue:
Considera un array di dimensioni (dn, dn-1, ... , d1) (d1 è la dimensione più piccola). Quando è disposto con riquadri di dimensioni
(tn, tn-1, ... , t1) (t1 è la dimensione minore), questo può essere descritto in termini di pad-rimodellazione-trasposizione nel seguente modo.
- L'array viene riempito in (⌈dn/tn⌉∙tn, ... , ⌈d1/t1⌉∙t1).
- Ogni dimensione i viene suddivisa (⌈di/ti⌉,
ti), ovvero l'array viene rimodellato in
(⌈dn/tn⌉, tn, ... , ⌈d1/t1⌉, t1).
La rimodellazione non presenta alcuna modifica fisica al layout, perciò è un processo di bitcast. Se non si pensa esplicitamente a un riquadro, questa rimodellazione potrebbe esprimere qualsiasi forma con lo stesso numero di elementi della forma imbottita; l'esempio qui è di come esprimere un riquadro in questo modo. - Una trasposizione avviene spostando tn, ... , t1 alle dimensioni minori, mantenendo al contempo l'ordine relativo, di modo che l'ordine delle dimensioni dalla maggiore alla più minore diventi
(⌈dn/tn⌉, ..., ⌈d1/t1⌉, tn, tn).
La forma finale ha il prefisso
(⌈dn/tn⌉, ... ,
⌈d1/t1⌉), che descrive il numero di riquadri in ogni dimensione. Un elemento dell'array (en, ... , e1) è mappato a questo elemento nella forma finale:
(⌊en/tn⌋, ... ,
⌊e0/t0⌋, en mod tn, ... ,
t1 mod). È facile vedere che l'indice lineare
dell'elemento segue la formula precedente come previsto.
Riquadri ripetuti
I riquadri XLA diventano ancora più flessibili applicandoli ripetutamente.
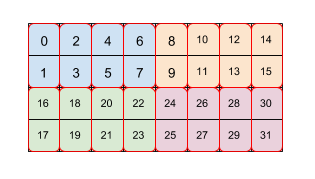
Figura 2
La Figura 2 mostra come un array di dimensioni 4 x 8 viene affiancato da due livelli di riquadro (prima 2 x 4 poi 2 x 1). Noi rappresentiamo questo tiling ripetuto come (2,4)(2,1). Ogni colore indica un riquadro 2 x 4 e ogni riquadro con bordo rosso è un riquadro 2 x 1. I numeri indicano l'indice lineare in memoria dell'elemento nel formato a mosaico. Questo formato corrisponde a quello utilizzato per BF16 su TPU, ad eccezione del fatto che il riquadro iniziale è più grande, ovvero il riquadro è (8,128)(2,1), dove lo scopo del secondo riquadro di 2x1 è raccogliere insieme due valori a 16 bit per formare un valore a 32 bit in modo da allinearsi all'architettura di una TPU.
Nota che un secondo riquadro o un riquadro successivo possono fare riferimento alle dimensioni minori all'interno del riquadro, riorganizzando solo i dati all'interno del riquadro, come in questo esempio con (8,128)(2,1), ma possono anche fare riferimento alle dimensioni trasversali principali del riquadro precedente.
Combinare dimensioni con i riquadri
I riquadri XLA supportano anche la combinazione di dimensioni. Ad esempio, può combinare le dimensioni in F32[2,7,8,11,10]{4,3,2,1,0} in F32[112,110]{1,0} prima di ti associarlo con (2,3). La piastrella utilizzata è (∗,∗,2,∗,3). In questo caso, l'asterisco in una tessera implica di prendere quella dimensione e di combinarla con la dimensione immediatamente più piccola. Più dimensioni adiacenti possono essere riassunte in un'unica dimensione. Una dimensione sottratta è rappresentata da un valore riquadro pari a -1 in quella dimensione del riquadro, che non è altrimenti valido in un riquadro come dimensione di dimensione.
Più precisamente, se la dimensione i della forma viene eliminata tramite un asterisco nel riquadro, prima che venga applicata la definizione precedente di riquadro, questa dimensione viene rimossa sia dalla forma affiancata sia dal vettore di riquadri e per la dimensione i-1 della forma il limite dell'array è aumentato da di-1 a didi-1. Questo passaggio viene ripetuto per ogni asterisco nel vettore di riquadro.
