چیدمان کاشی کاری شده

XLA TPU به دلیل ماهیت دوبعدی رجیسترهای برداری خود، از فرمت‌های متنوعی مبتنی بر کاشی استفاده می‌کند.

قالب‌های کاشی‌کاری شده

قالب کاشی‌کاری، یک شکل را به کاشی‌هایی (معمولاً یک بعدی یا دو بعدی) تجزیه می‌کند. کاشی‌ها در حافظه به ترتیب از بزرگ به کوچک (طرح اصلی ردیفی) چیده می‌شوند. در داخل یک کاشی، عناصر نیز به ترتیب از بزرگ به کوچک چیده می‌شوند.

شکل ۱

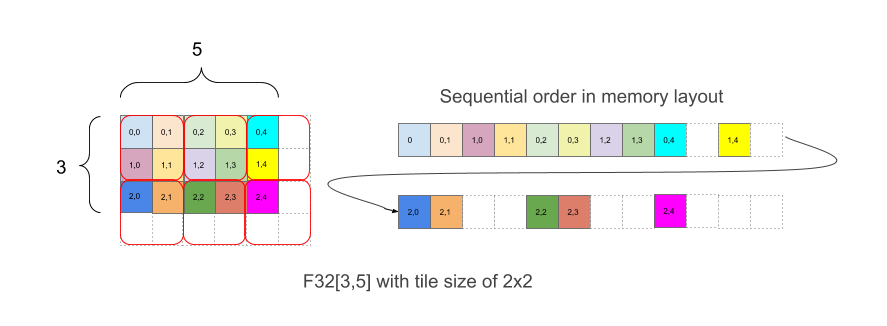
شکل ۱ نشان می‌دهد که چگونه یک آرایه F32[3,5] با کاشی‌کاری ۲x۲ در حافظه قرار می‌گیرد. شکلی با این طرح‌بندی به صورت F32[3,5]{1,0:T(2,2)} نوشته می‌شود، که در آن ۱,۰ مربوط به ترتیب فیزیکی ابعاد است (فیلد minor_to_major در طرح‌بندی) در حالی که (۲,۲) بعد از دونقطه نشان دهنده کاشی‌کاری ابعاد فیزیکی با کاشی ۲x۲ است.

به طور شهودی، کاشی‌ها برای پوشاندن شکل چیده می‌شوند و سپس درون هر کاشی، عناصر بدون کاشی‌کاری چیده می‌شوند، مانند مثال بالا، که در آن قسمت سمت راست مثال، طرح‌بندی در حافظه را نشان می‌دهد، از جمله عناصر padding سفید که برای داشتن کاشی‌های کامل ۲x۲ اضافه شده‌اند، حتی اگر مرزهای آرایه اصلی زوج نباشند.

عناصر اضافی در padding لازم نیست حاوی مقدار خاصی باشند.

فرمول‌های شاخص خطی برای کاشی‌کاری با توجه به شکل و نوع کاشی

بدون کاشی‌کاری، یک عنصر e=(en _n , e _n-1 , ... , e ₁ ) در یک آرایه با مرزهای آرایه d=(d _n , d _n-1 , ... , d ₁ ) (d1 کوچکترین بُعد است) به ترتیب از بزرگ به کوچک در موقعیت قرار می‌گیرد:

شاخص_خطی(ه، د)
= linear_index((en _n ، en _n-1 ، ...، e ₁ )، (d _n ، d _n-1 ، ...، d ₁ ))
= _{پایان و} د _ن-۱ ... د _۱ + د _{ن ن-۱} د _ن-۲ ... د _۱ + ... + د _۱

برای سادگی نمادگذاری در این سند، فرض می‌کنیم که یک کاشی دارای همان تعداد ابعاد آرایه است. در پیاده‌سازی کاشی‌کاری XLA، این امر به کاشی‌کاری‌هایی با ابعاد کمتر تعمیم داده می‌شود، به این صورت که ابعاد اصلی اولیه بدون تغییر باقی می‌مانند و کاشی‌کاری فقط برای ابعاد فرعی اعمال می‌شود، به طوری که کاشی‌کاری مشخص شده، پسوندی از ابعاد فیزیکی شکلی که کاشی‌کاری می‌شود را ذکر می‌کند.

وقتی از کاشی‌کاری با اندازه (t _n ، t _n-1 ، ...، t ₁ ) استفاده می‌شود، یک عنصر در آرایه با اندیس‌های (en _n ، en _n-1 ، ...، e ₁ ) به این موقعیت در طرح نهایی نگاشت می‌شود:

تابع (e, d, t) با استفاده از کاشی، اندیس خطی (linear_index_with_tile) را نمایش می‌دهد.
= linear_index((⌊e/t⌋, e mod t), (⌈d/t⌉, t)) (محاسبات به صورت عنصر به عنصر است، (a,b) الحاق است)
= linear_index((⌊e _n /t _n ⌋, ... , ⌊e ₁ /t ₁ ⌋, en _n mod t _n , ... , e ₁ mod t ₁ ), (⌈d _n /t _n ⌉, ... , ⌈d ₁ /t ₁ ⌉, t _n , t _n-1 , ... , t ₁ ))
= linear_index((⌊e _n /t _n ⌋, ... , ⌊e ₁ /t ₁ ⌋), (⌈d _n /t _n ⌉, ... , ⌈d ₁ /t ₁ ⌉))∙t _n t _n-1 ...t ₁ + linear_index((en _n mod t _n , ... , e ₁ mod t ₁ ), (t _n , t _n-1 , ... , t ₁ ))

می‌توان طرح‌بندی را دارای دو بخش در نظر گرفت: (⌊e _n /t _n ⌋, ... , ⌊e ₁ /t ₁ ⌋) که مربوط به یک شاخص کاشی در آرایه‌ای از کاشی‌ها با اندازه (⌈d _n /t _n ⌉, ... , ⌈d ₁ /t ₁ ⌉) است و (en _n mod t _n , ... , e ₁ mod t ₁ ) که مربوط به یک شاخص درون کاشی است. تابع ceil در ⌈d _i /t _i ⌉ ظاهر می‌شود زیرا اگر کاشی‌ها از مرزهای آرایه بزرگتر تجاوز کنند، مانند شکل 1، padding درج می‌شود. هم کاشی‌ها و هم عناصر درون کاشی‌ها به صورت بازگشتی و بدون کاشی‌کاری طرح‌بندی می‌شوند.

برای مثال در شکل 1، عنصر (2،3) برای یک بردار مختصات ترکیبی (1،1،0،1) دارای اندیس کاشی (1،1) و اندیس درون کاشی (0،1) است. اندیس‌های کاشی دارای کران (2،3) هستند و خود کاشی برای یک بردار ترکیبی (2،3،2،2) برابر با (2،2) است. اندیس خطی با کاشی برای عنصری با اندیس (2،3) در شکل منطقی به صورت زیر است:

linear_index_with_tile((2،3)، (3،5)، (2،2))
= شاخص_خطی((1،1،0،1)، (2،3،2،2))
= شاخص_خطی((1،1)، (2،3)) ∙ 2 ∙ 2 + شاخص_خطی((0،1)، (2،2))
= (۱ ∙ ۳ + ۱) ∙ ۲ ∙ ۲ + (۰ ∙ ۲ + ۱)
= ۱۷.

\[ LinearIndexWithTile((2,3), (3,5), (2,2)) \\ = LinearIndex((1,1,0,1), (2,3,2,2)) \\ = LinearIndex((1,1), (2,3)) \cdot 2 \cdot 2 + LinearIndex((0,1), (2,2)) \\ = (1 \cdot 3 + 1) \cdot 2 \cdot 2 + (0 \cdot 2 + 1) \\ = 17 \]

کاشی‌کاری به صورت پد-تغییر شکل-جابجایی

طرح‌بندی مبتنی بر کاشی‌کاری به شرح زیر عمل می‌کند:
آرایه‌ای با ابعاد ( _dn ، dn _-1 ، ...، d1) را در نظر بگیرید (d1 کوچکترین بُعد است). وقتی با کاشی‌کاری به اندازه ( _tn ، tn _-1 ، ...، _t1 ) ( _t1 کوچکترین بُعد است) طرح‌بندی شود، آن کاشی‌کاری را می‌توان بر اساس پد-تغییرشکل-ترانپوز به روش زیر توصیف کرد.

1. آرایه به (⌈d _n /t _n ⌉∙t _n , ... , ⌈d ₁ /t ₁ ⌉∙t ₁ ) پر شده است.
2. هر بُعد i به (⌈d _i /t i ⌉, t _i ) شکسته می‌شود، یعنی آرایه به صورت زیر تغییر شکل می‌دهد.
   (⌈d _n /t _n ⌉، t _n ، ...، ⌈d ₁ /t ₁ ⌉، t ₁ ).
   هیچ تغییر فیزیکی در طرح‌بندی این تغییر شکل به خودی خود وجود ندارد، بنابراین این تغییر شکل یک bitcast است. اگر کسی صراحتاً به کاشی‌کاری فکر نکند، این تغییر شکل می‌تواند هر شکلی را با همان تعداد عناصر شکل padded بیان کند - مثال اینجا نحوه بیان یک کاشی به این روش است.
3. یک ترانهاده با حرکت دادن t _n ، ...، t ₁ به جزئی‌ترین ابعاد و در عین حال حفظ ترتیب نسبی آنها اتفاق می‌افتد، به طوری که ترتیب ابعاد از اصلی‌ترین به فرعی‌ترین به صورت زیر می‌شود:
   (⌈d _n /t _n ⌉، ...، ⌈d ₁ /t ₁ ⌉، t _n ، ...، t ₁ ).

شکل نهایی پیشوند دارد
(⌈d _n /t _n ⌉, ... , ⌈d ₁ /t ₁ ⌉) که تعداد کاشی‌ها را در هر بعد توصیف می‌کند. یک عنصر در آرایه (en _n , ... , e ₁ ) به این عنصر در شکل نهایی نگاشت می‌شود:
(⌊e _n /t _n ⌋, ... , ⌊e ₀ /t ₀ ⌋, _{en n} mod t _n , ... , e ₁ mod t ₁ ). به راحتی می‌توان دید که ضریب خطی عنصر، همانطور که انتظار می‌رود، از فرمول بالا پیروی می‌کند.

کاشی‌کاری مکرر

کاشی‌کاری XLA با استفاده مکرر از آن، انعطاف‌پذیرتر هم می‌شود.

شکل ۲

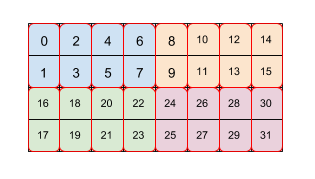
شکل ۲ نشان می‌دهد که چگونه یک آرایه با اندازه ۴x۸ با دو سطح کاشی‌کاری (ابتدا ۲x۴ و سپس ۲x۱) کاشی‌کاری شده است. ما این کاشی‌کاری تکراری را به صورت (۲,۴)(۲,۱) نمایش می‌دهیم. هر رنگ نشان دهنده یک کاشی ۲x۴ و هر کادر مرزی قرمز یک کاشی ۲x۱ است. اعداد نشان دهنده اندیس خطی در حافظه آن عنصر در قالب کاشی‌کاری شده هستند. این قالب با قالب مورد استفاده برای BF16 در TPU مطابقت دارد، با این تفاوت که کاشی اولیه بزرگتر است، یعنی کاشی‌کاری به صورت (۸,۱۲۸)(۲,۱) است، که در آن هدف از کاشی‌کاری دوم با ۲x۱، جمع‌آوری دو مقدار ۱۶ بیتی برای تشکیل یک مقدار ۳۲ بیتی به روشی است که با معماری یک TPU همسو باشد.

توجه داشته باشید که یک کاشی دوم یا بعدی می‌تواند به ابعاد فرعی درون کاشی اشاره داشته باشد، که فقط داده‌ها را درون کاشی بازآرایی می‌کند، همانطور که در این مثال با (8,128)(2,1) آمده است، اما می‌تواند به ابعاد اصلی متقاطع کاشی از کاشی‌کاری قبلی نیز اشاره داشته باشد.

ترکیب ابعاد با استفاده از کاشی

کاشی‌کاری XLA همچنین از ترکیب ابعاد پشتیبانی می‌کند. برای مثال، می‌تواند ابعاد موجود در F32[2,7,8,11,10]{4,3,2,1,0} را ابتدا در F32[112,110]{1,0} ترکیب کند و سپس آن را با (2,3) کاشی‌کاری کند. کاشی مورد استفاده (*,*,2,*,3) است. در اینجا علامت ستاره در یک کاشی به معنای گرفتن آن بُعد و ترکیب آن با بُعد فرعی‌تر بعدی است. چندین بُعد مجاور را می‌توان در یک بُعد ادغام کرد. یک بُعد ادغام‌شده با مقدار کاشی -1 در آن بُعد کاشی نشان داده می‌شود، که در غیر این صورت در یک کاشی به عنوان اندازه بُعد معتبر نیست.

به طور دقیق‌تر، اگر بُعد i از شکل از طریق یک ستاره در کاشی حذف شود، قبل از اعمال تعریف قبلی کاشی‌کاری، آن بُعد هم از شکلی که کاشی‌کاری می‌شود و هم از بردار کاشی حذف می‌شود و آنچه بُعد i-1 شکل بوده، مرز آرایه‌ای آن از d _i-1 به d _i d _i-1 افزایش می‌یابد. این مرحله برای هر ستاره در بردار کاشی تکرار می‌شود.

نمونه‌هایی از قالب‌های کاشی‌کاری

این بخش نمونه‌هایی از فرمت‌های محبوب XLA را نشان می‌دهد.

1. قالب تا شده - اکثر آرایه‌هایی که روی TPU نیستند از قالب خطی تا شده استفاده می‌کنند، مانند مثلاً C++.
2. قالب کاشی TPU - رایج‌ترین قالب در XLA/TPU، کاشی‌کاری با ابعاد 8x128 است که با رجیسترهای برداری 32 بیتی 8x128 در یک TPU مطابقت دارد.
3. قالب کاشی کوچک TPU (معروف به "طرح‌بندی کوچک دوم فشرده") - وقتی اندازه دومین بعد کوچک ۱ یا ۲ باشد، کاشی‌های XLA/TPU به جای آن به اندازه 2x128 کاشی می‌شوند تا در حافظه صرفه‌جویی شود زیرا یک کاشی 2x128 از یک کاشی 8x128 کوچکتر است. وقتی اندازه دومین بعد کوچک ۳ یا ۴ باشد، کاشی‌های XLA/TPU به اندازه 4x128 کاشی می‌شوند.
4. قالب کاشی ۱۶ بیتی TPU - وقتی نوع عنصر آرایه BF16 باشد، کاشی‌هایی که استفاده می‌کنیم معمولاً (8,128)(2,1) هستند. سطح دوم کاشی‌کاری، به اصطلاح بسته‌بندی BF16 را انجام می‌دهد. همانطور که در شکل ۲ بالا می‌بینید، یک عنصر از یک ردیف زوج و یک عنصر از یک ردیف فرد با هم چیده شده و در یک عنصر ۳۲ بیتی قرار می‌گیرند. این قالب به این دلیل استفاده می‌شود که TPUها به صورت بومی با مقادیر ۳۲ بیتی کار می‌کنند و انتقال داده‌ها از طریق دومین بُعد فرعی بسیار کارآمدتر از انتقال داده‌ها از طریق کوچکترین بُعد است، بنابراین جمع‌آوری دو مقدار ۱۶ بیتی برای دریافت ۳۲ بیت از یک ستون بسیار کارآمدتر از انجام آن به روش واضح‌تر گرفتن دو مقدار ۱۶ بیتی از یک ردیف است.
5. قالب کاشی 8 بیتی TPU - قالب اینجا بسیار شبیه به قالب 16 بیتی است، تفاوت فقط این است که ما باید 4 عنصر را برای بدست آوردن 32 بیت به جای فقط دو بیت جمع کنیم، بنابراین کاشی کاری به صورت (8,128)(4,1) در می‌آید.
6. قالب کاشی تک بیتی TPU - TPUها در حال حاضر از ۱ بایت برای یک مقدار بولی استفاده می‌کنند، یعنی اندازه عنصر PRED بر حسب بایت ۱ است. استفاده از کاشی‌کاری به صورت (32,128)(32,1) و استفاده از تنها ۱ بیت برای هر عنصر، اتلاف کمتری خواهد داشت.