ওভারভিউ
টেনসরের অনির্দিষ্ট শার্ডিং (বা টেনসরের নির্দিষ্ট মাত্রা) অনুমান করার জন্য শার্ডিং প্রচার ব্যবহারকারী-নির্দিষ্ট শার্ডিং ব্যবহার করে। এটি গণনা গ্রাফের ডেটা প্রবাহকে (ব্যবহার-ডিফ চেইন) উভয় দিকেই অতিক্রম করে যতক্ষণ না একটি নির্দিষ্ট বিন্দুতে পৌঁছায়, অর্থাৎ, পূর্ববর্তী শার্ডিং সিদ্ধান্তগুলি পূর্বাবস্থায় না নিয়ে শার্ডিং আর পরিবর্তন করতে পারে না।
বংশবৃদ্ধি ধাপে পচনশীল হতে পারে। প্রতিটি ধাপে একটি নির্দিষ্ট অপারেশনের দিকে তাকানো এবং সেই অপারেশনের বৈশিষ্ট্যের উপর ভিত্তি করে টেনসর (অপারেন্ড এবং ফলাফল) এর মধ্যে প্রচার করা জড়িত। একটি উদাহরণ হিসাবে একটি matmul নিলে, আমরা ফলাফলের সংশ্লিষ্ট মাত্রার সাথে lhs বা rhs-এর অ-কন্ট্রাক্টিং মাত্রার মধ্যে বা lhs এবং rhs-এর সংকোচনশীল মাত্রার মধ্যে প্রচার করব।
একটি অপারেশনের বৈশিষ্ট্যগুলি এর ইনপুট এবং আউটপুটগুলিতে সংশ্লিষ্ট মাত্রাগুলির মধ্যে সংযোগ নির্ধারণ করে এবং অপ শার্ডিং নিয়ম অনুসারে বিমূর্ত করা যেতে পারে।
বিরোধ নিষ্পত্তি ছাড়াই, বিবাদমান অক্ষগুলিকে উপেক্ষা করার সময় একটি প্রচার পদক্ষেপ কেবল যতটা সম্ভব প্রচার করবে; আমরা এটিকে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শার্ডিং অক্ষ হিসাবে উল্লেখ করি।
বিস্তারিত ডিজাইন
দ্বন্দ্ব সমাধানের অনুক্রম
আমরা একটি অনুক্রমের মধ্যে একাধিক দ্বন্দ্ব সমাধানের কৌশল রচনা করি:
- ব্যবহারকারী সংজ্ঞায়িত অগ্রাধিকার . শার্ডিং রিপ্রেজেন্টেশনে , আমরা বর্ণনা করেছি কিভাবে প্রোগ্রামের ক্রমবর্ধমান বিভাজন করার জন্য ডাইমেনশন শার্ডিংয়ের সাথে অগ্রাধিকার যুক্ত করা যেতে পারে, যেমন, ব্যাচ প্যারালেলিজম -> মেগাট্রন -> জিরো শার্ডিং করা। এটি পুনরাবৃত্তিতে প্রচার প্রয়োগ করে অর্জন করা হয় - পুনরাবৃত্তি
iএ আমরা সমস্ত ডাইমেনশন শার্ডিংগুলি প্রচার করি যেগুলির অগ্রাধিকার<=iএবং অন্য সকলকে উপেক্ষা করি৷ আমরা এটাও নিশ্চিত করি যে প্রচারটি ব্যবহারকারীর সংজ্ঞায়িত শার্ডিংগুলিকে নিম্ন অগ্রাধিকার (>i) দিয়ে ওভাররাইড করবে না, এমনকি যদি সেগুলি পূর্ববর্তী পুনরাবৃত্তির সময় উপেক্ষা করা হয়। - অপারেশন ভিত্তিক অগ্রাধিকার । আমরা অপারেশন ধরনের উপর ভিত্তি করে shardings প্রচার. "পাস-থ্রু" ক্রিয়াকলাপগুলির (যেমন, উপাদান-ভিত্তিক ক্রিয়াকলাপ এবং পুনঃআকৃতি) সর্বোচ্চ অগ্রাধিকার রয়েছে, যখন আকৃতির রূপান্তর (যেমন, ডট এবং হ্রাস) সহ ক্রিয়াকলাপগুলির অগ্রাধিকার কম থাকে৷
- আক্রমণাত্মক প্রচার। একটি আক্রমনাত্মক কৌশল সঙ্গে shardings প্রচার করুন. মৌলিক কৌশল শুধুমাত্র দ্বন্দ্ব ছাড়াই শার্ডিং প্রচার করে, যখন আক্রমনাত্মক কৌশল দ্বন্দ্বের সমাধান করে। উচ্চ আক্রমনাত্মকতা সম্ভাব্য যোগাযোগ খরচ মেমরি পদচিহ্ন কমাতে পারে.
- মৌলিক প্রচার। এটি শ্রেণিবিন্যাসের মধ্যে প্রচারের সর্বনিম্ন কৌশল, যা কোনও বিরোধের সমাধান করে না এবং পরিবর্তে সমস্ত অপারেন্ড এবং ফলাফলের মধ্যে সামঞ্জস্যপূর্ণ অক্ষগুলিকে প্রচার করে।

এই অনুক্রমটিকে লুপগুলির জন্য নেস্টেড হিসাবে ব্যাখ্যা করা যেতে পারে। উদাহরণস্বরূপ, প্রতিটি ব্যবহারকারীর অগ্রাধিকারের জন্য, একটি সম্পূর্ণ অপ-অগ্রাধিকার প্রচার প্রয়োগ করা হয়।
অপারেশন শার্ডিং নিয়ম
শার্ডিং নিয়ম প্রতিটি ক্রিয়াকলাপের একটি বিমূর্ততা প্রবর্তন করে যা নির্দিষ্ট অপারেশনের ধরন এবং তাদের বৈশিষ্ট্যগুলি সম্পর্কে যুক্তি ছাড়াই অপারেন্ড থেকে ফলাফল বা অপারেন্ড জুড়ে শার্ডিংগুলি প্রচার করার জন্য প্রয়োজনীয় তথ্য সহ প্রকৃত প্রচার অ্যালগরিদম সরবরাহ করে। এটি মূলত অপ-নির্দিষ্ট যুক্তিকে ফ্যাক্টর করে এবং শুধুমাত্র প্রচারের উদ্দেশ্যে সমস্ত অপের জন্য একটি ভাগ করা প্রতিনিধিত্ব (ডেটা স্ট্রাকচার) প্রদান করে। এর সহজতম আকারে, এটি কেবল এই ফাংশনটি সরবরাহ করে:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
নিয়মটি আমাদের এই ডেটা স্ট্রাকচারের ( OpShardingRule ) উপর ভিত্তি করে শুধুমাত্র একবারই প্রপাগেশন অ্যালগরিদম লিখতে দেয়, অনেক অপ্স জুড়ে একই ধরনের কোডের প্রতিলিপি করার পরিবর্তে, অপস জুড়ে বাগ বা অসামঞ্জস্যপূর্ণ আচরণের সম্ভাবনাকে ব্যাপকভাবে হ্রাস করে।
মাতমুল উদাহরণে ফিরে যাওয়া যাক।
একটি এনকোডিং যা প্রচারের সময় প্রয়োজনীয় তথ্যগুলিকে এনক্যাপসুলেট করে, অর্থাৎ, মাত্রার মধ্যে সম্পর্ক, ইন্সাম নোটেশন আকারে লেখা যেতে পারে:
(i, k), (k, j) -> (i, j)
এই এনকোডিংয়ে, প্রতিটি মাত্রা একটি একক ফ্যাক্টরের সাথে ম্যাপ করা হয়।
কীভাবে প্রচার এই ম্যাপিংটি ব্যবহার করে: যদি একটি অক্ষের সাথে একটি অপারেন্ড/ফলাফলের একটি মাত্রা সংক্ষিপ্ত করা হয়, তবে প্রচার এই ম্যাপিংয়ে সেই মাত্রার ফ্যাক্টরটি সন্ধান করবে এবং একই ফ্যাক্টর সহ অন্যান্য অপারেন্ড/ফ্যাক্টরকে তাদের নিজ নিজ মাত্রার সাথে সংক্ষিপ্ত করবে - এবং (প্রতিলিপি সম্পর্কে পূর্বের আলোচনার সাপেক্ষে) যেগুলি সম্ভাব্যতা/অপারেন্ডের ফলাফলগুলিও সম্ভব নয়। যে অক্ষ বরাবর
যৌগিক কারণ: পুনঃআকৃতির জন্য নিয়ম প্রসারিত করা
অনেক অপারেশনে, যেমন, মাটমুল, আমাদের শুধুমাত্র প্রতিটি মাত্রাকে একটি একক ফ্যাক্টরে ম্যাপ করতে হবে। যাইহোক, এটি পুনর্নির্মাণের জন্য যথেষ্ট নয়।
নিম্নলিখিত পুনঃআকৃতি একটিতে দুটি মাত্রাকে একত্রিত করে:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
এখানে, ইনপুটের 0 এবং 1 উভয় মাত্রাই আউটপুটের 0 মাত্রার সাথে মিলে যায়। বলুন আমরা ইনপুটকে ফ্যাক্টর দিয়ে শুরু করি:
(i,j,k) : i=2, j=4, k=32
আপনি দেখতে পারেন যে আমরা যদি আউটপুটের জন্য একই কারণগুলি ব্যবহার করতে চাই, তবে একাধিক কারণের উল্লেখ করার জন্য আমাদের একটি একক মাত্রার প্রয়োজন হবে:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
যদি পুনঃআকৃতি একটি মাত্রা বিভক্ত করা হয় তবে একই কাজ করা যেতে পারে:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
এখানে,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
এখানে সাইজ 8 এর ডাইমেনশনটি মূলত 2 এবং 4 ফ্যাক্টর নিয়ে গঠিত, তাই আমরা ফ্যাক্টরগুলোকে (i,j,k) ফ্যাক্টর বলছি।
এই কারণগুলি এমন ক্ষেত্রেও কাজ করতে পারে যেখানে কোনও একটি কারণের সাথে সামঞ্জস্যপূর্ণ কোনও সম্পূর্ণ মাত্রা নেই:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
এই উদাহরণটিও জোর দেয় যে কেন আমাদের ফ্যাক্টরের আকারগুলি সংরক্ষণ করতে হবে - যেহেতু আমরা সংশ্লিষ্ট মাত্রাগুলি থেকে সেগুলি সহজেই অনুমান করতে পারি না।
মূল প্রচার অ্যালগরিদম
ফ্যাক্টর বরাবর shardings প্রচার করুন
শার্ডিতে, আমাদের কাছে টেনসর, মাত্রা এবং কারণের অনুক্রম রয়েছে। তারা বিভিন্ন স্তরে ডেটা প্রতিনিধিত্ব করে। একটি গুণনীয়ক একটি উপ-মাত্রা। এটি একটি অভ্যন্তরীণ শ্রেণিবিন্যাস যা শার্ডিং প্রচারে ব্যবহৃত হয়। প্রতিটি মাত্রা এক বা একাধিক কারণের সাথে সঙ্গতিপূর্ণ হতে পারে। মাত্রা এবং ফ্যাক্টরের মধ্যে ম্যাপিং OpShardingRule দ্বারা সংজ্ঞায়িত করা হয়।

শার্ডি মাত্রার পরিবর্তে ফ্যাক্টর বরাবর শার্ডিং অক্ষগুলি প্রচার করে । এটি করার জন্য, নীচের চিত্রে দেখানো হিসাবে আমাদের তিনটি ধাপ রয়েছে:
- প্রজেক্ট
DimShardingথেকেFactorSharding -
FactorShardingএর স্পেসে শার্ডিং অক্ষগুলি প্রচার করুন - আপডেট করা
DimShardingপেতে আপডেট করাFactorShardingপ্রজেক্ট করুন
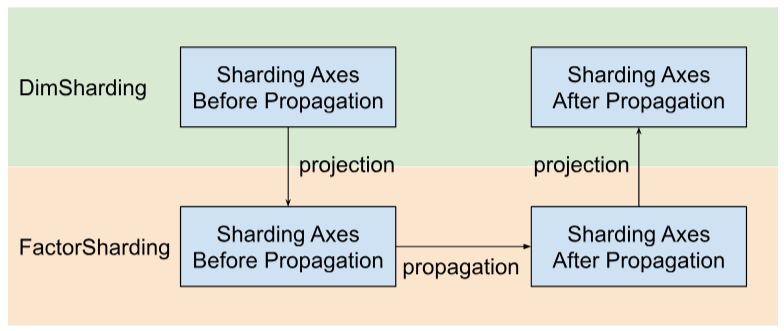
ফ্যাক্টর বরাবর Sharding প্রচারের ভিজ্যুয়ালাইজেশন
আমরা শার্ডিং প্রচারের সমস্যা এবং অ্যালগরিদম কল্পনা করতে নিম্নলিখিত টেবিলটি ব্যবহার করব।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | ||||
| T1 | ||||
| T2 |
- প্রতিটি কলাম একটি ফ্যাক্টর প্রতিনিধিত্ব করে। F0 মানে সূচক 0 সহ ফ্যাক্টর। আমরা ফ্যাক্টর (কলাম) বরাবর শার্ডিং প্রচার করি।
- প্রতিটি সারি একটি টেনসর প্রতিনিধিত্ব করে। T0 সূচক 0 সহ টেনসরকে বোঝায়। টেনসর হল সমস্ত অপারেন্ড এবং একটি নির্দিষ্ট অপারেশনের জন্য জড়িত ফলাফল। এক সারিতে অক্ষগুলি ওভারল্যাপ করতে পারে না। একটি অক্ষ (বা উপ-অক্ষ) একটি টেনসরকে বহুবার বিভাজন করতে ব্যবহার করা যায় না। যদি একটি অক্ষ স্পষ্টভাবে প্রতিলিপি করা হয়, আমরা টেনসরকে বিভাজন করতে এটি ব্যবহার করতে পারি না।
সুতরাং, প্রতিটি কোষ একটি ফ্যাক্টর শার্ডিং প্রতিনিধিত্ব করে। আংশিক টেনসরে একটি ফ্যাক্টর অনুপস্থিত হতে পারে। C = dot(A, B) এর জন্য টেবিলটি নীচে রয়েছে। একটি N ধারণকারী কোষগুলি বোঝায় যে ফ্যাক্টরটি টেনসরে নেই। উদাহরণস্বরূপ, F2 T1 এবং T2 তে আছে, কিন্তু T0 তে নয়।
C = dot(A, B) | F0 ব্যাচিং আবছা | F1 নন-কন্ট্রাক্টিং ডিম | F2 নন-কন্ট্রাক্টিং ডিম | F3 কন্ট্রাক্টিং ডিম | স্পষ্টভাবে প্রতিলিপি করা অক্ষ |
|---|---|---|---|---|---|
| T0 = A | এন | ||||
| T1 = B | এন | ||||
| T2 = C | এন |
শার্ডিং অক্ষ সংগ্রহ এবং প্রচার করুন
আমরা বিস্তার কল্পনা করার জন্য নীচে দেখানো একটি সহজ উদাহরণ ব্যবহার করি।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | "একটি" | "চ" | ||
| T1 | "ক", "বি" | "গ", "ডি" | "g" | |
| T2 | "গ", "ই" |
ধাপ 1. প্রতিটি ফ্যাক্টর (ওরফে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শার্ডিং অক্ষ) বরাবর প্রচার করার জন্য অক্ষগুলি খুঁজুন। এই উদাহরণের জন্য, আমরা F0 বরাবর ["a", "b"] প্রচার করি, F1 বরাবর ["c"] প্রচার করি এবং F2 বরাবর কিছুই প্রচার করি না।
ধাপ 2. নিম্নলিখিত ফলাফল পেতে ফ্যাক্টর শার্ডিংগুলি প্রসারিত করুন।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | "ক", "বি" | "গ" | "চ" | |
| T1 | "ক", "বি" | "গ", "ডি" | "g" | |
| T2 | "ক", "বি" | "গ", "ই" |
ডেটা প্রবাহ অপস
উপরোক্ত প্রচারের ধাপের বর্ণনাটি বেশিরভাগ অপারেশনের ক্ষেত্রে প্রযোজ্য। যাইহোক, এমন কিছু ক্ষেত্রে রয়েছে যেখানে একটি শার্ডিং নিয়ম উপযুক্ত নয়। এই ক্ষেত্রে, Shardy ডেটা ফ্লো অপ্স সংজ্ঞায়িত করে।
কিছু অপ X-এর একটি ডেটা প্রবাহ প্রান্ত উৎসের একটি সেট এবং লক্ষ্যগুলির একটি সেটের মধ্যে একটি সেতুকে সংজ্ঞায়িত করে, যেমন সমস্ত উত্স এবং লক্ষ্যগুলিকে একইভাবে শার্ড করা উচিত। এই ধরনের অপারেশনগুলির উদাহরণ হল stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp এবং এছাড়াও sdy::ManualComputationOp । পরিশেষে, ShardableDataFlowOpInterface প্রয়োগ করে এমন যেকোনো অপকে ডেটা ফ্লো অপ হিসেবে বিবেচনা করা হয়।
একটি অপের একাধিক ডেটা প্রবাহ প্রান্ত থাকতে পারে যা একে অপরের সাথে অর্থোগোনাল। যেমন:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
যখন op-এর n ডেটা ফ্লো প্রান্ত রয়েছে: i-th ডেটা প্রবাহ প্রান্তগুলি উত্স x_i , return_value_i এবং লক্ষ্য y_i , pred_arg_i , body_arg_i মধ্যে রয়েছে।
Shardy একটি ডেটা ফ্লো প্রান্তের সমস্ত উৎস এবং লক্ষ্যগুলির মধ্যে শার্ডিংগুলি প্রচার করবে যেন এটি একটি নিয়মিত অপারেন্ড হিসাবে উত্সগুলি এবং ফলাফল হিসাবে লক্ষ্যগুলি এবং একটি পরিচয় sdy.op_sharding_rule ৷ তার মানে ফরোয়ার্ড প্রচার হচ্ছে উৎস থেকে লক্ষ্যে এবং পেছনের প্রচার হচ্ছে লক্ষ্য থেকে উৎসে।
ব্যবহারকারীর দ্বারা বেশ কয়েকটি পদ্ধতি প্রয়োগ করা আবশ্যক যেগুলি বর্ণনা করে যে কীভাবে তাদের মালিকের মাধ্যমে প্রতিটি ডেটা ফ্লো প্রান্তের উত্স এবং লক্ষ্যগুলি পেতে হয় এবং কীভাবে প্রান্তের মালিকদের শার্ডিংগুলি পেতে এবং সেট করতে হয়৷ শার্ডির প্রচারে ব্যবহৃত ডাটা ফ্লো প্রান্তের একজন মালিক একজন ব্যবহারকারী-নির্দিষ্ট লক্ষ্য। ব্যবহারকারী এটি নির্বিচারে চয়ন করতে পারেন তবে এটি স্থির হওয়া দরকার।
উদাহরণস্বরূপ, নিম্নে সংজ্ঞায়িত custom_op দেওয়া:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
এই কাস্টম_অপের ডেটা ফ্লো প্রান্তের জন্য দুটি প্রকার রয়েছে: n প্রান্তগুলি প্রতিটি return_value_i (উৎস) এবং y_i (লক্ষ্য) এবং n প্রান্তগুলি x_i (উত্স) এবং body_arg_i (লক্ষ্যগুলি) এর মধ্যে। এই ক্ষেত্রে, প্রান্ত মালিকদের লক্ষ্য হিসাবে একই।
ওভারভিউ
টেনসরের অনির্দিষ্ট শার্ডিং (বা টেনসরের নির্দিষ্ট মাত্রা) অনুমান করার জন্য শার্ডিং প্রচার ব্যবহারকারী-নির্দিষ্ট শার্ডিং ব্যবহার করে। এটি গণনা গ্রাফের ডেটা প্রবাহকে (ব্যবহার-ডিফ চেইন) উভয় দিকেই অতিক্রম করে যতক্ষণ না একটি নির্দিষ্ট বিন্দুতে পৌঁছায়, অর্থাৎ, পূর্ববর্তী শার্ডিং সিদ্ধান্তগুলি পূর্বাবস্থায় না নিয়ে শার্ডিং আর পরিবর্তন করতে পারে না।
বংশবৃদ্ধি ধাপে পচনশীল হতে পারে। প্রতিটি ধাপে একটি নির্দিষ্ট অপারেশনের দিকে তাকানো এবং সেই অপারেশনের বৈশিষ্ট্যের উপর ভিত্তি করে টেনসর (অপারেন্ড এবং ফলাফল) এর মধ্যে প্রচার করা জড়িত। একটি উদাহরণ হিসাবে একটি matmul নিলে, আমরা ফলাফলের সংশ্লিষ্ট মাত্রার সাথে lhs বা rhs-এর অ-কন্ট্রাক্টিং মাত্রার মধ্যে বা lhs এবং rhs-এর সংকোচনশীল মাত্রার মধ্যে প্রচার করব।
একটি অপারেশনের বৈশিষ্ট্যগুলি এর ইনপুট এবং আউটপুটগুলিতে সংশ্লিষ্ট মাত্রাগুলির মধ্যে সংযোগ নির্ধারণ করে এবং অপ শার্ডিং নিয়ম অনুসারে বিমূর্ত করা যেতে পারে।
বিরোধ নিষ্পত্তি ছাড়াই, বিবাদমান অক্ষগুলিকে উপেক্ষা করার সময় একটি প্রচার পদক্ষেপ কেবল যতটা সম্ভব প্রচার করবে; আমরা এটিকে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শার্ডিং অক্ষ হিসাবে উল্লেখ করি।
বিস্তারিত ডিজাইন
দ্বন্দ্ব সমাধানের অনুক্রম
আমরা একটি অনুক্রমের মধ্যে একাধিক দ্বন্দ্ব সমাধানের কৌশল রচনা করি:
- ব্যবহারকারী সংজ্ঞায়িত অগ্রাধিকার . শার্ডিং রিপ্রেজেন্টেশনে , আমরা বর্ণনা করেছি কিভাবে প্রোগ্রামের ক্রমবর্ধমান বিভাজন করার জন্য ডাইমেনশন শার্ডিংয়ের সাথে অগ্রাধিকার যুক্ত করা যেতে পারে, যেমন, ব্যাচ প্যারালেলিজম -> মেগাট্রন -> জিরো শার্ডিং করা। এটি পুনরাবৃত্তিতে প্রচার প্রয়োগ করে অর্জন করা হয় - পুনরাবৃত্তি
iএ আমরা সমস্ত ডাইমেনশন শার্ডিংগুলি প্রচার করি যেগুলির অগ্রাধিকার<=iএবং অন্য সকলকে উপেক্ষা করি৷ আমরা এটাও নিশ্চিত করি যে প্রচারটি ব্যবহারকারীর সংজ্ঞায়িত শার্ডিংগুলিকে নিম্ন অগ্রাধিকার (>i) দিয়ে ওভাররাইড করবে না, এমনকি যদি সেগুলি পূর্ববর্তী পুনরাবৃত্তির সময় উপেক্ষা করা হয়। - অপারেশন ভিত্তিক অগ্রাধিকার । আমরা অপারেশন ধরনের উপর ভিত্তি করে shardings প্রচার. "পাস-থ্রু" ক্রিয়াকলাপগুলির (যেমন, উপাদান-ভিত্তিক ক্রিয়াকলাপ এবং পুনঃআকৃতি) সর্বোচ্চ অগ্রাধিকার রয়েছে, যখন আকৃতির রূপান্তর (যেমন, ডট এবং হ্রাস) সহ ক্রিয়াকলাপগুলির অগ্রাধিকার কম থাকে৷
- আক্রমণাত্মক প্রচার। একটি আক্রমনাত্মক কৌশল সঙ্গে shardings প্রচার করুন. মৌলিক কৌশল শুধুমাত্র দ্বন্দ্ব ছাড়াই শার্ডিং প্রচার করে, যখন আক্রমনাত্মক কৌশল দ্বন্দ্বের সমাধান করে। উচ্চ আক্রমনাত্মকতা সম্ভাব্য যোগাযোগ খরচ মেমরি পদচিহ্ন কমাতে পারে.
- মৌলিক প্রচার। এটি শ্রেণিবিন্যাসের মধ্যে প্রচারের সর্বনিম্ন কৌশল, যা কোনও বিরোধের সমাধান করে না এবং পরিবর্তে সমস্ত অপারেন্ড এবং ফলাফলের মধ্যে সামঞ্জস্যপূর্ণ অক্ষগুলিকে প্রচার করে।

এই অনুক্রমটিকে লুপগুলির জন্য নেস্টেড হিসাবে ব্যাখ্যা করা যেতে পারে। উদাহরণস্বরূপ, প্রতিটি ব্যবহারকারীর অগ্রাধিকারের জন্য, একটি সম্পূর্ণ অপ-অগ্রাধিকার প্রচার প্রয়োগ করা হয়।
অপারেশন শার্ডিং নিয়ম
শার্ডিং নিয়ম প্রতিটি ক্রিয়াকলাপের একটি বিমূর্ততা প্রবর্তন করে যা নির্দিষ্ট অপারেশনের ধরন এবং তাদের বৈশিষ্ট্যগুলি সম্পর্কে যুক্তি ছাড়াই অপারেন্ড থেকে ফলাফল বা অপারেন্ড জুড়ে শার্ডিংগুলি প্রচার করার জন্য প্রয়োজনীয় তথ্য সহ প্রকৃত প্রচার অ্যালগরিদম সরবরাহ করে। এটি মূলত অপ-নির্দিষ্ট যুক্তিকে ফ্যাক্টর করে এবং শুধুমাত্র প্রচারের উদ্দেশ্যে সমস্ত অপের জন্য একটি ভাগ করা প্রতিনিধিত্ব (ডেটা স্ট্রাকচার) প্রদান করে। এর সহজতম আকারে, এটি কেবল এই ফাংশনটি সরবরাহ করে:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
নিয়মটি আমাদের এই ডেটা স্ট্রাকচারের ( OpShardingRule ) উপর ভিত্তি করে শুধুমাত্র একবারই প্রপাগেশন অ্যালগরিদম লিখতে দেয়, অনেক অপ্স জুড়ে একই ধরনের কোডের প্রতিলিপি করার পরিবর্তে, অপস জুড়ে বাগ বা অসামঞ্জস্যপূর্ণ আচরণের সম্ভাবনাকে ব্যাপকভাবে হ্রাস করে।
মাতমুল উদাহরণে ফিরে যাওয়া যাক।
একটি এনকোডিং যা প্রচারের সময় প্রয়োজনীয় তথ্যগুলিকে এনক্যাপসুলেট করে, অর্থাৎ, মাত্রার মধ্যে সম্পর্ক, ইন্সাম নোটেশন আকারে লেখা যেতে পারে:
(i, k), (k, j) -> (i, j)
এই এনকোডিংয়ে, প্রতিটি মাত্রা একটি একক ফ্যাক্টরের সাথে ম্যাপ করা হয়।
কীভাবে প্রচার এই ম্যাপিংটি ব্যবহার করে: যদি একটি অক্ষের সাথে একটি অপারেন্ড/ফলাফলের একটি মাত্রা সংক্ষিপ্ত করা হয়, তবে প্রচার এই ম্যাপিংয়ে সেই মাত্রার ফ্যাক্টরটি সন্ধান করবে এবং একই ফ্যাক্টর সহ অন্যান্য অপারেন্ড/ফ্যাক্টরকে তাদের নিজ নিজ মাত্রার সাথে সংক্ষিপ্ত করবে - এবং (প্রতিলিপি সম্পর্কে পূর্বের আলোচনার সাপেক্ষে) যেগুলি সম্ভাব্যতা/অপারেন্ডের ফলাফলগুলিও সম্ভব নয়। যে অক্ষ বরাবর
যৌগিক কারণ: পুনঃআকৃতির জন্য নিয়ম প্রসারিত করা
অনেক অপারেশনে, যেমন, মাটমুল, আমাদের শুধুমাত্র প্রতিটি মাত্রাকে একটি একক ফ্যাক্টরে ম্যাপ করতে হবে। যাইহোক, এটি পুনর্নির্মাণের জন্য যথেষ্ট নয়।
নিম্নলিখিত পুনঃআকৃতি একটিতে দুটি মাত্রাকে একত্রিত করে:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
এখানে, ইনপুটের 0 এবং 1 উভয় মাত্রাই আউটপুটের 0 মাত্রার সাথে মিলে যায়। বলুন আমরা ইনপুটকে ফ্যাক্টর দিয়ে শুরু করি:
(i,j,k) : i=2, j=4, k=32
আপনি দেখতে পারেন যে আমরা যদি আউটপুটের জন্য একই কারণগুলি ব্যবহার করতে চাই, তবে একাধিক কারণের উল্লেখ করার জন্য আমাদের একটি একক মাত্রার প্রয়োজন হবে:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
যদি পুনঃআকৃতি একটি মাত্রা বিভক্ত করা হয় তবে একই কাজ করা যেতে পারে:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
এখানে,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
এখানে সাইজ 8 এর ডাইমেনশনটি মূলত 2 এবং 4 ফ্যাক্টর নিয়ে গঠিত, তাই আমরা ফ্যাক্টরগুলোকে (i,j,k) ফ্যাক্টর বলছি।
এই কারণগুলি এমন ক্ষেত্রেও কাজ করতে পারে যেখানে কোনও একটি কারণের সাথে সামঞ্জস্যপূর্ণ কোনও সম্পূর্ণ মাত্রা নেই:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
এই উদাহরণটিও জোর দেয় যে কেন আমাদের ফ্যাক্টরের আকারগুলি সংরক্ষণ করতে হবে - যেহেতু আমরা সংশ্লিষ্ট মাত্রাগুলি থেকে সেগুলি সহজেই অনুমান করতে পারি না।
মূল প্রচার অ্যালগরিদম
ফ্যাক্টর বরাবর shardings প্রচার করুন
শার্ডিতে, আমাদের কাছে টেনসর, মাত্রা এবং কারণের অনুক্রম রয়েছে। তারা বিভিন্ন স্তরে ডেটা প্রতিনিধিত্ব করে। একটি গুণনীয়ক একটি উপ-মাত্রা। এটি একটি অভ্যন্তরীণ শ্রেণিবিন্যাস যা শার্ডিং প্রচারে ব্যবহৃত হয়। প্রতিটি মাত্রা এক বা একাধিক কারণের সাথে সঙ্গতিপূর্ণ হতে পারে। মাত্রা এবং ফ্যাক্টরের মধ্যে ম্যাপিং OpShardingRule দ্বারা সংজ্ঞায়িত করা হয়।

শার্ডি মাত্রার পরিবর্তে ফ্যাক্টর বরাবর শার্ডিং অক্ষগুলি প্রচার করে । এটি করার জন্য, নীচের চিত্রে দেখানো হিসাবে আমাদের তিনটি ধাপ রয়েছে:
- প্রজেক্ট
DimShardingথেকেFactorSharding -
FactorShardingএর স্পেসে শার্ডিং অক্ষগুলি প্রচার করুন - আপডেট করা
DimShardingপেতে আপডেট করাFactorShardingপ্রজেক্ট করুন

ফ্যাক্টর বরাবর Sharding প্রচারের ভিজ্যুয়ালাইজেশন
আমরা শার্ডিং প্রচারের সমস্যা এবং অ্যালগরিদম কল্পনা করতে নিম্নলিখিত টেবিলটি ব্যবহার করব।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | ||||
| T1 | ||||
| T2 |
- প্রতিটি কলাম একটি ফ্যাক্টর প্রতিনিধিত্ব করে। F0 মানে সূচক 0 সহ ফ্যাক্টর। আমরা ফ্যাক্টর (কলাম) বরাবর শার্ডিং প্রচার করি।
- প্রতিটি সারি একটি টেনসর প্রতিনিধিত্ব করে। T0 সূচক 0 সহ টেনসরকে বোঝায়। টেনসর হল সমস্ত অপারেন্ড এবং একটি নির্দিষ্ট অপারেশনের জন্য জড়িত ফলাফল। এক সারিতে অক্ষগুলি ওভারল্যাপ করতে পারে না। একটি অক্ষ (বা উপ-অক্ষ) একটি টেনসরকে বহুবার বিভাজন করতে ব্যবহার করা যায় না। যদি একটি অক্ষ স্পষ্টভাবে প্রতিলিপি করা হয়, আমরা টেনসরকে বিভাজন করতে এটি ব্যবহার করতে পারি না।
সুতরাং, প্রতিটি কোষ একটি ফ্যাক্টর শার্ডিং প্রতিনিধিত্ব করে। আংশিক টেনসরে একটি ফ্যাক্টর অনুপস্থিত হতে পারে। C = dot(A, B) এর জন্য টেবিলটি নীচে রয়েছে। একটি N ধারণকারী কোষগুলি বোঝায় যে ফ্যাক্টরটি টেনসরে নেই। উদাহরণস্বরূপ, F2 T1 এবং T2 তে আছে, কিন্তু T0 তে নয়।
C = dot(A, B) | F0 ব্যাচিং আবছা | F1 নন-কন্ট্রাক্টিং ডিম | F2 নন-কন্ট্রাক্টিং ডিম | F3 কন্ট্রাক্টিং ডিম | স্পষ্টভাবে প্রতিলিপি করা অক্ষ |
|---|---|---|---|---|---|
| T0 = A | এন | ||||
| T1 = B | এন | ||||
| T2 = C | এন |
শার্ডিং অক্ষ সংগ্রহ এবং প্রচার করুন
আমরা বিস্তার কল্পনা করার জন্য নীচে দেখানো একটি সহজ উদাহরণ ব্যবহার করি।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | "একটি" | "চ" | ||
| T1 | "ক", "বি" | "গ", "ডি" | "g" | |
| T2 | "গ", "ই" |
ধাপ 1. প্রতিটি ফ্যাক্টর (ওরফে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শার্ডিং অক্ষ) বরাবর প্রচার করার জন্য অক্ষগুলি খুঁজুন। এই উদাহরণের জন্য, আমরা F0 বরাবর ["a", "b"] প্রচার করি, F1 বরাবর ["c"] প্রচার করি এবং F2 বরাবর কিছুই প্রচার করি না।
ধাপ 2. নিম্নলিখিত ফলাফল পেতে ফ্যাক্টর শার্ডিংগুলি প্রসারিত করুন।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | "ক", "বি" | "গ" | "চ" | |
| T1 | "ক", "বি" | "গ", "ডি" | "g" | |
| T2 | "ক", "বি" | "গ", "ই" |
ডেটা প্রবাহ অপস
উপরোক্ত প্রচারের ধাপের বর্ণনাটি বেশিরভাগ অপারেশনের ক্ষেত্রে প্রযোজ্য। যাইহোক, এমন কিছু ক্ষেত্রে রয়েছে যেখানে একটি শার্ডিং নিয়ম উপযুক্ত নয়। এই ক্ষেত্রে, Shardy ডেটা ফ্লো অপ্স সংজ্ঞায়িত করে।
কিছু অপ X-এর একটি ডেটা প্রবাহ প্রান্ত উৎসের একটি সেট এবং লক্ষ্যগুলির একটি সেটের মধ্যে একটি সেতুকে সংজ্ঞায়িত করে, যেমন সমস্ত উত্স এবং লক্ষ্যগুলিকে একইভাবে শার্ড করা উচিত। এই ধরনের অপারেশনগুলির উদাহরণ হল stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp এবং এছাড়াও sdy::ManualComputationOp । পরিশেষে, ShardableDataFlowOpInterface প্রয়োগ করে এমন যেকোনো অপকে ডেটা ফ্লো অপ হিসেবে বিবেচনা করা হয়।
একটি অপের একাধিক ডেটা প্রবাহ প্রান্ত থাকতে পারে যা একে অপরের সাথে অর্থোগোনাল। যেমন:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
যখন op-এর n ডেটা ফ্লো প্রান্ত রয়েছে: i-th ডেটা প্রবাহ প্রান্তগুলি উত্স x_i , return_value_i এবং লক্ষ্য y_i , pred_arg_i , body_arg_i মধ্যে রয়েছে।
Shardy একটি ডেটা ফ্লো প্রান্তের সমস্ত উৎস এবং লক্ষ্যগুলির মধ্যে শার্ডিংগুলি প্রচার করবে যেন এটি একটি নিয়মিত অপারেন্ড হিসাবে উত্সগুলি এবং ফলাফল হিসাবে লক্ষ্যগুলি এবং একটি পরিচয় sdy.op_sharding_rule ৷ তার মানে ফরোয়ার্ড প্রচার হচ্ছে উৎস থেকে লক্ষ্যে এবং পেছনের প্রচার হচ্ছে লক্ষ্য থেকে উৎসে।
ব্যবহারকারীর দ্বারা বেশ কয়েকটি পদ্ধতি প্রয়োগ করা আবশ্যক যেগুলি বর্ণনা করে যে কীভাবে তাদের মালিকের মাধ্যমে প্রতিটি ডেটা ফ্লো প্রান্তের উত্স এবং লক্ষ্যগুলি পেতে হয় এবং কীভাবে প্রান্তের মালিকদের শার্ডিংগুলি পেতে এবং সেট করতে হয়৷ শার্ডির প্রচারে ব্যবহৃত ডাটা ফ্লো প্রান্তের একজন মালিক একজন ব্যবহারকারী-নির্দিষ্ট লক্ষ্য। ব্যবহারকারী এটি নির্বিচারে চয়ন করতে পারেন তবে এটি স্থির হওয়া দরকার।
উদাহরণস্বরূপ, নিম্নে সংজ্ঞায়িত custom_op দেওয়া:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
এই কাস্টম_অপের ডেটা ফ্লো প্রান্তের জন্য দুটি প্রকার রয়েছে: n প্রান্তগুলি প্রতিটি return_value_i (উৎস) এবং y_i (লক্ষ্য) এবং n প্রান্তগুলি x_i (উত্স) এবং body_arg_i (লক্ষ্যগুলি) এর মধ্যে। এই ক্ষেত্রে, প্রান্ত মালিকদের লক্ষ্য হিসাবে একই।
ওভারভিউ
টেনসরের অনির্দিষ্ট শার্ডিং (বা টেনসরের নির্দিষ্ট মাত্রা) অনুমান করার জন্য শার্ডিং প্রচার ব্যবহারকারী-নির্দিষ্ট শার্ডিং ব্যবহার করে। এটি গণনা গ্রাফের ডেটা প্রবাহকে (ব্যবহার-ডিফ চেইন) উভয় দিকেই অতিক্রম করে যতক্ষণ না একটি নির্দিষ্ট বিন্দুতে পৌঁছায়, অর্থাৎ, পূর্ববর্তী শার্ডিং সিদ্ধান্তগুলি পূর্বাবস্থায় না নিয়ে শার্ডিং আর পরিবর্তন করতে পারে না।
বংশবৃদ্ধি ধাপে পচনশীল হতে পারে। প্রতিটি ধাপে একটি নির্দিষ্ট অপারেশনের দিকে তাকানো এবং সেই অপারেশনের বৈশিষ্ট্যের উপর ভিত্তি করে টেনসর (অপারেন্ড এবং ফলাফল) এর মধ্যে প্রচার করা জড়িত। একটি উদাহরণ হিসাবে একটি matmul নিলে, আমরা ফলাফলের সংশ্লিষ্ট মাত্রার সাথে lhs বা rhs-এর অ-কন্ট্রাক্টিং মাত্রার মধ্যে বা lhs এবং rhs-এর সংকোচনশীল মাত্রার মধ্যে প্রচার করব।
একটি অপারেশনের বৈশিষ্ট্যগুলি এর ইনপুট এবং আউটপুটগুলিতে সংশ্লিষ্ট মাত্রাগুলির মধ্যে সংযোগ নির্ধারণ করে এবং অপ শার্ডিং নিয়ম অনুসারে বিমূর্ত করা যেতে পারে।
বিরোধ নিষ্পত্তি ছাড়াই, বিবাদমান অক্ষগুলিকে উপেক্ষা করার সময় একটি প্রচার পদক্ষেপ কেবল যতটা সম্ভব প্রচার করবে; আমরা এটিকে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শার্ডিং অক্ষ হিসাবে উল্লেখ করি।
বিস্তারিত ডিজাইন
দ্বন্দ্ব সমাধানের অনুক্রম
আমরা একটি অনুক্রমের মধ্যে একাধিক দ্বন্দ্ব সমাধানের কৌশল রচনা করি:
- ব্যবহারকারী সংজ্ঞায়িত অগ্রাধিকার . শার্ডিং রিপ্রেজেন্টেশনে , আমরা বর্ণনা করেছি কিভাবে প্রোগ্রামের ক্রমবর্ধমান বিভাজন করার জন্য ডাইমেনশন শার্ডিংয়ের সাথে অগ্রাধিকার যুক্ত করা যেতে পারে, যেমন, ব্যাচ প্যারালেলিজম -> মেগাট্রন -> জিরো শার্ডিং করা। এটি পুনরাবৃত্তিতে প্রচার প্রয়োগ করে অর্জন করা হয় - পুনরাবৃত্তি
iএ আমরা সমস্ত ডাইমেনশন শার্ডিংগুলি প্রচার করি যেগুলির অগ্রাধিকার<=iএবং অন্য সকলকে উপেক্ষা করি৷ আমরা এটাও নিশ্চিত করি যে প্রচারটি ব্যবহারকারীর সংজ্ঞায়িত শার্ডিংগুলিকে নিম্ন অগ্রাধিকার (>i) দিয়ে ওভাররাইড করবে না, এমনকি যদি সেগুলি পূর্ববর্তী পুনরাবৃত্তির সময় উপেক্ষা করা হয়। - অপারেশন ভিত্তিক অগ্রাধিকার । আমরা অপারেশন ধরনের উপর ভিত্তি করে shardings প্রচার. "পাস-থ্রু" ক্রিয়াকলাপগুলির (যেমন, উপাদান-ভিত্তিক ক্রিয়াকলাপ এবং পুনঃআকৃতি) সর্বোচ্চ অগ্রাধিকার রয়েছে, যখন আকৃতির রূপান্তর (যেমন, ডট এবং হ্রাস) সহ ক্রিয়াকলাপগুলির অগ্রাধিকার কম থাকে৷
- আক্রমণাত্মক প্রচার। একটি আক্রমনাত্মক কৌশল সঙ্গে shardings প্রচার করুন. মৌলিক কৌশল শুধুমাত্র দ্বন্দ্ব ছাড়াই শার্ডিং প্রচার করে, যখন আক্রমনাত্মক কৌশল দ্বন্দ্বের সমাধান করে। উচ্চ আক্রমনাত্মকতা সম্ভাব্য যোগাযোগ খরচ মেমরি পদচিহ্ন কমাতে পারে.
- মৌলিক প্রচার। এটি শ্রেণিবিন্যাসের মধ্যে প্রচারের সর্বনিম্ন কৌশল, যা কোনও বিরোধের সমাধান করে না এবং পরিবর্তে সমস্ত অপারেন্ড এবং ফলাফলের মধ্যে সামঞ্জস্যপূর্ণ অক্ষগুলিকে প্রচার করে।

এই অনুক্রমটিকে লুপগুলির জন্য নেস্টেড হিসাবে ব্যাখ্যা করা যেতে পারে। উদাহরণস্বরূপ, প্রতিটি ব্যবহারকারীর অগ্রাধিকারের জন্য, একটি সম্পূর্ণ অপ-অগ্রাধিকার প্রচার প্রয়োগ করা হয়।
অপারেশন শার্ডিং নিয়ম
শার্ডিং নিয়ম প্রতিটি ক্রিয়াকলাপের একটি বিমূর্ততা প্রবর্তন করে যা নির্দিষ্ট অপারেশনের ধরন এবং তাদের বৈশিষ্ট্যগুলি সম্পর্কে যুক্তি ছাড়াই অপারেন্ড থেকে ফলাফল বা অপারেন্ড জুড়ে শার্ডিংগুলি প্রচার করার জন্য প্রয়োজনীয় তথ্য সহ প্রকৃত প্রচার অ্যালগরিদম সরবরাহ করে। এটি মূলত অপ-নির্দিষ্ট যুক্তিকে ফ্যাক্টর করে এবং শুধুমাত্র প্রচারের উদ্দেশ্যে সমস্ত অপের জন্য একটি ভাগ করা প্রতিনিধিত্ব (ডেটা স্ট্রাকচার) প্রদান করে। এর সহজতম আকারে, এটি কেবল এই ফাংশনটি সরবরাহ করে:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
নিয়মটি আমাদের এই ডেটা স্ট্রাকচারের ( OpShardingRule ) উপর ভিত্তি করে শুধুমাত্র একবারই প্রপাগেশন অ্যালগরিদম লিখতে দেয়, অনেক অপ্স জুড়ে একই ধরনের কোডের প্রতিলিপি করার পরিবর্তে, অপস জুড়ে বাগ বা অসামঞ্জস্যপূর্ণ আচরণের সম্ভাবনাকে ব্যাপকভাবে হ্রাস করে।
মাতমুল উদাহরণে ফিরে যাওয়া যাক।
একটি এনকোডিং যা প্রচারের সময় প্রয়োজনীয় তথ্যগুলিকে এনক্যাপসুলেট করে, অর্থাৎ, মাত্রার মধ্যে সম্পর্ক, ইন্সাম নোটেশন আকারে লেখা যেতে পারে:
(i, k), (k, j) -> (i, j)
এই এনকোডিংয়ে, প্রতিটি মাত্রা একটি একক ফ্যাক্টরের সাথে ম্যাপ করা হয়।
কীভাবে প্রচার এই ম্যাপিংটি ব্যবহার করে: যদি একটি অক্ষের সাথে একটি অপারেন্ড/ফলাফলের একটি মাত্রা সংক্ষিপ্ত করা হয়, তবে প্রচার এই ম্যাপিংয়ে সেই মাত্রার ফ্যাক্টরটি সন্ধান করবে এবং একই ফ্যাক্টর সহ অন্যান্য অপারেন্ড/ফ্যাক্টরকে তাদের নিজ নিজ মাত্রার সাথে সংক্ষিপ্ত করবে - এবং (প্রতিলিপি সম্পর্কে পূর্বের আলোচনার সাপেক্ষে) যেগুলি সম্ভাব্যতা/অপারেন্ডের ফলাফলগুলিও সম্ভব নয়। যে অক্ষ বরাবর
যৌগিক কারণ: পুনঃআকৃতির জন্য নিয়ম প্রসারিত করা
অনেক অপারেশনে, যেমন, মাটমুল, আমাদের শুধুমাত্র প্রতিটি মাত্রাকে একটি একক ফ্যাক্টরে ম্যাপ করতে হবে। যাইহোক, এটি পুনর্নির্মাণের জন্য যথেষ্ট নয়।
নিম্নলিখিত পুনঃআকৃতি একটিতে দুটি মাত্রাকে একত্রিত করে:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
এখানে, ইনপুটের 0 এবং 1 উভয় মাত্রাই আউটপুটের 0 মাত্রার সাথে মিলে যায়। বলুন আমরা ইনপুটকে ফ্যাক্টর দিয়ে শুরু করি:
(i,j,k) : i=2, j=4, k=32
আপনি দেখতে পারেন যে আমরা যদি আউটপুটের জন্য একই কারণগুলি ব্যবহার করতে চাই, তবে একাধিক কারণের উল্লেখ করার জন্য আমাদের একটি একক মাত্রার প্রয়োজন হবে:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
যদি পুনঃআকৃতি একটি মাত্রা বিভক্ত করা হয় তবে একই কাজ করা যেতে পারে:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
এখানে,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
এখানে সাইজ 8 এর ডাইমেনশনটি মূলত 2 এবং 4 ফ্যাক্টর নিয়ে গঠিত, তাই আমরা ফ্যাক্টরগুলোকে (i,j,k) ফ্যাক্টর বলছি।
এই কারণগুলি এমন ক্ষেত্রেও কাজ করতে পারে যেখানে কোনও একটি কারণের সাথে সামঞ্জস্যপূর্ণ কোনও সম্পূর্ণ মাত্রা নেই:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
এই উদাহরণটিও জোর দেয় যে কেন আমাদের ফ্যাক্টরের আকারগুলি সংরক্ষণ করতে হবে - যেহেতু আমরা সংশ্লিষ্ট মাত্রাগুলি থেকে সেগুলি সহজেই অনুমান করতে পারি না।
মূল প্রচার অ্যালগরিদম
ফ্যাক্টর বরাবর shardings প্রচার করুন
শার্ডিতে, আমাদের কাছে টেনসর, মাত্রা এবং কারণের অনুক্রম রয়েছে। তারা বিভিন্ন স্তরে ডেটা প্রতিনিধিত্ব করে। একটি গুণনীয়ক একটি উপ-মাত্রা। এটি একটি অভ্যন্তরীণ শ্রেণিবিন্যাস যা শার্ডিং প্রচারে ব্যবহৃত হয়। প্রতিটি মাত্রা এক বা একাধিক কারণের সাথে সঙ্গতিপূর্ণ হতে পারে। মাত্রা এবং ফ্যাক্টরের মধ্যে ম্যাপিং OpShardingRule দ্বারা সংজ্ঞায়িত করা হয়।

শার্ডি মাত্রার পরিবর্তে ফ্যাক্টর বরাবর শার্ডিং অক্ষগুলি প্রচার করে । এটি করার জন্য, নীচের চিত্রে দেখানো হিসাবে আমাদের তিনটি ধাপ রয়েছে:
- প্রজেক্ট
DimShardingথেকেFactorSharding -
FactorShardingএর স্পেসে শার্ডিং অক্ষগুলি প্রচার করুন - আপডেট করা
DimShardingপেতে আপডেট করাFactorShardingপ্রজেক্ট করুন

ফ্যাক্টর বরাবর Sharding প্রচারের ভিজ্যুয়ালাইজেশন
আমরা শার্ডিং প্রচারের সমস্যা এবং অ্যালগরিদম কল্পনা করতে নিম্নলিখিত টেবিলটি ব্যবহার করব।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | ||||
| T1 | ||||
| T2 |
- প্রতিটি কলাম একটি ফ্যাক্টর প্রতিনিধিত্ব করে। F0 মানে সূচক 0 সহ ফ্যাক্টর। আমরা ফ্যাক্টর (কলাম) বরাবর শার্ডিং প্রচার করি।
- প্রতিটি সারি একটি টেনসর প্রতিনিধিত্ব করে। T0 সূচক 0 সহ টেনসরকে বোঝায়। টেনসর হল সমস্ত অপারেন্ড এবং একটি নির্দিষ্ট অপারেশনের জন্য জড়িত ফলাফল। এক সারিতে অক্ষগুলি ওভারল্যাপ করতে পারে না। একটি অক্ষ (বা উপ-অক্ষ) একটি টেনসরকে বহুবার বিভাজন করতে ব্যবহার করা যায় না। যদি একটি অক্ষ স্পষ্টভাবে প্রতিলিপি করা হয়, আমরা টেনসরকে বিভাজন করতে এটি ব্যবহার করতে পারি না।
সুতরাং, প্রতিটি কোষ একটি ফ্যাক্টর শার্ডিং প্রতিনিধিত্ব করে। আংশিক টেনসরে একটি ফ্যাক্টর অনুপস্থিত হতে পারে। C = dot(A, B) এর জন্য টেবিলটি নীচে রয়েছে। একটি N ধারণকারী কোষগুলি বোঝায় যে ফ্যাক্টরটি টেনসরে নেই। উদাহরণস্বরূপ, F2 T1 এবং T2 তে আছে, কিন্তু T0 তে নয়।
C = dot(A, B) | F0 ব্যাচিং আবছা | F1 নন-কন্ট্রাক্টিং ডিম | F2 নন-কন্ট্রাক্টিং ডিম | F3 কন্ট্রাক্টিং ডিম | স্পষ্টভাবে প্রতিলিপি করা অক্ষ |
|---|---|---|---|---|---|
| T0 = A | এন | ||||
| T1 = B | এন | ||||
| T2 = C | এন |
শার্ডিং অক্ষ সংগ্রহ এবং প্রচার করুন
আমরা বিস্তার কল্পনা করার জন্য নীচে দেখানো একটি সহজ উদাহরণ ব্যবহার করি।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | "একটি" | "চ" | ||
| T1 | "ক", "বি" | "গ", "ডি" | "g" | |
| T2 | "গ", "ই" |
ধাপ 1. প্রতিটি ফ্যাক্টর (ওরফে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শার্ডিং অক্ষ) বরাবর প্রচার করার জন্য অক্ষগুলি খুঁজুন। এই উদাহরণের জন্য, আমরা F0 বরাবর ["a", "b"] প্রচার করি, F1 বরাবর ["c"] প্রচার করি এবং F2 বরাবর কিছুই প্রচার করি না।
ধাপ 2. নিম্নলিখিত ফলাফল পেতে ফ্যাক্টর শার্ডিংগুলি প্রসারিত করুন।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি করা অক্ষ | |
|---|---|---|---|---|
| T0 | "ক", "বি" | "গ" | "চ" | |
| T1 | "ক", "বি" | "গ", "ডি" | "g" | |
| T2 | "ক", "বি" | "গ", "ই" |
ডেটা প্রবাহ অপস
উপরোক্ত প্রচারের ধাপের বর্ণনাটি বেশিরভাগ অপারেশনের ক্ষেত্রে প্রযোজ্য। যাইহোক, এমন কিছু ক্ষেত্রে রয়েছে যেখানে একটি শার্ডিং নিয়ম উপযুক্ত নয়। এই ক্ষেত্রে, Shardy ডেটা ফ্লো অপ্স সংজ্ঞায়িত করে।
কিছু অপ X-এর একটি ডেটা প্রবাহ প্রান্ত উৎসের একটি সেট এবং লক্ষ্যগুলির একটি সেটের মধ্যে একটি সেতুকে সংজ্ঞায়িত করে, যেমন সমস্ত উত্স এবং লক্ষ্যগুলিকে একইভাবে শার্ড করা উচিত। এই ধরনের অপারেশনগুলির উদাহরণ হল stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp এবং এছাড়াও sdy::ManualComputationOp । পরিশেষে, ShardableDataFlowOpInterface প্রয়োগ করে এমন যেকোনো অপকে ডেটা ফ্লো অপ হিসেবে বিবেচনা করা হয়।
একটি অপের একাধিক ডেটা প্রবাহ প্রান্ত থাকতে পারে যা একে অপরের সাথে অর্থোগোনাল। যেমন:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
যখন op-এর n ডেটা ফ্লো প্রান্ত রয়েছে: i-th ডেটা প্রবাহ প্রান্তগুলি উত্স x_i , return_value_i এবং লক্ষ্য y_i , pred_arg_i , body_arg_i মধ্যে রয়েছে।
Shardy একটি ডেটা ফ্লো প্রান্তের সমস্ত উৎস এবং লক্ষ্যগুলির মধ্যে শার্ডিংগুলি প্রচার করবে যেন এটি একটি নিয়মিত অপারেন্ড হিসাবে উত্সগুলি এবং ফলাফল হিসাবে লক্ষ্যগুলি এবং একটি পরিচয় sdy.op_sharding_rule ৷ তার মানে ফরোয়ার্ড প্রচার হচ্ছে উৎস থেকে লক্ষ্যে এবং পেছনের প্রচার হচ্ছে লক্ষ্য থেকে উৎসে।
ব্যবহারকারীর দ্বারা বেশ কয়েকটি পদ্ধতি প্রয়োগ করা আবশ্যক যেগুলি বর্ণনা করে যে কীভাবে তাদের মালিকের মাধ্যমে প্রতিটি ডেটা ফ্লো প্রান্তের উত্স এবং লক্ষ্যগুলি পেতে হয় এবং কীভাবে প্রান্তের মালিকদের শার্ডিংগুলি পেতে এবং সেট করতে হয়৷ শার্ডির প্রচারে ব্যবহৃত ডাটা ফ্লো প্রান্তের একজন মালিক একজন ব্যবহারকারী-নির্দিষ্ট লক্ষ্য। ব্যবহারকারী এটি নির্বিচারে চয়ন করতে পারেন তবে এটি স্থির হওয়া দরকার।
উদাহরণস্বরূপ, নিম্নে সংজ্ঞায়িত custom_op দেওয়া:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
এই কাস্টম_অপের ডেটা ফ্লো প্রান্তের জন্য দুটি প্রকার রয়েছে: n প্রান্তগুলি প্রতিটি return_value_i (উৎস) এবং y_i (লক্ষ্য) এবং n প্রান্তগুলি x_i (উত্স) এবং body_arg_i (লক্ষ্যগুলি) এর মধ্যে। এই ক্ষেত্রে, প্রান্ত মালিকদের লক্ষ্য হিসাবে একই।
ওভারভিউ
টেনসরের অনির্দিষ্ট শার্ডিং (বা টেনসরের নির্দিষ্ট মাত্রা) অনুমান করার জন্য শার্ডিং প্রচার ব্যবহারকারী-নির্দিষ্ট শার্ডিং ব্যবহার করে। এটি গণনা গ্রাফের ডেটা প্রবাহকে (ব্যবহার-ডিফ চেইন) উভয় দিকেই অতিক্রম করে যতক্ষণ না একটি নির্দিষ্ট বিন্দুতে পৌঁছায়, অর্থাৎ, পূর্ববর্তী শার্ডিং সিদ্ধান্তগুলি পূর্বাবস্থায় না নিয়ে শার্ডিং আর পরিবর্তন করতে পারে না।
বংশবৃদ্ধি ধাপে পচনশীল হতে পারে। প্রতিটি ধাপে একটি নির্দিষ্ট অপারেশনের দিকে তাকানো এবং সেই অপারেশনের বৈশিষ্ট্যের উপর ভিত্তি করে টেনসর (অপারেন্ড এবং ফলাফল) এর মধ্যে প্রচার করা জড়িত। একটি উদাহরণ হিসাবে একটি matmul নিলে, আমরা ফলাফলের সংশ্লিষ্ট মাত্রার সাথে lhs বা rhs-এর অ-কন্ট্রাক্টিং মাত্রার মধ্যে বা lhs এবং rhs-এর সংকোচনশীল মাত্রার মধ্যে প্রচার করব।
একটি অপারেশনের বৈশিষ্ট্যগুলি এর ইনপুট এবং আউটপুটগুলিতে সংশ্লিষ্ট মাত্রাগুলির মধ্যে সংযোগ নির্ধারণ করে এবং অপ শার্ডিং নিয়ম অনুসারে বিমূর্ত করা যেতে পারে।
বিরোধ নিষ্পত্তি ছাড়াই, বিবাদমান অক্ষগুলিকে উপেক্ষা করার সময় একটি প্রচার পদক্ষেপ কেবল যতটা সম্ভব প্রচার করবে; আমরা এটিকে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শার্ডিং অক্ষ হিসাবে উল্লেখ করি।
বিস্তারিত ডিজাইন
দ্বন্দ্ব সমাধানের অনুক্রম
আমরা একটি অনুক্রমের মধ্যে একাধিক দ্বন্দ্ব সমাধানের কৌশল রচনা করি:
- ব্যবহারকারী সংজ্ঞায়িত অগ্রাধিকার . শার্ডিং রিপ্রেজেন্টেশনে , আমরা বর্ণনা করেছি কিভাবে প্রোগ্রামের ক্রমবর্ধমান বিভাজন করার জন্য ডাইমেনশন শার্ডিংয়ের সাথে অগ্রাধিকার যুক্ত করা যেতে পারে, যেমন, ব্যাচ প্যারালেলিজম -> মেগাট্রন -> জিরো শার্ডিং করা। এটি পুনরাবৃত্তিতে প্রচার প্রয়োগ করে অর্জন করা হয় - পুনরাবৃত্তি
iএ আমরা সমস্ত ডাইমেনশন শার্ডিংগুলি প্রচার করি যেগুলির অগ্রাধিকার<=iএবং অন্য সকলকে উপেক্ষা করি৷ আমরা এটাও নিশ্চিত করি যে প্রচারটি ব্যবহারকারীর সংজ্ঞায়িত শার্ডিংগুলিকে নিম্ন অগ্রাধিকার (>i) দিয়ে ওভাররাইড করবে না, এমনকি যদি সেগুলি পূর্ববর্তী পুনরাবৃত্তির সময় উপেক্ষা করা হয়। - অপারেশন ভিত্তিক অগ্রাধিকার । আমরা অপারেশন ধরনের উপর ভিত্তি করে shardings প্রচার. "পাস-থ্রু" ক্রিয়াকলাপগুলির (যেমন, উপাদান-ভিত্তিক ক্রিয়াকলাপ এবং পুনঃআকৃতি) সর্বোচ্চ অগ্রাধিকার রয়েছে, যখন আকৃতির রূপান্তর (যেমন, ডট এবং হ্রাস) সহ ক্রিয়াকলাপগুলির অগ্রাধিকার কম থাকে৷
- আক্রমণাত্মক প্রচার। একটি আক্রমনাত্মক কৌশল সঙ্গে shardings প্রচার করুন. মৌলিক কৌশল শুধুমাত্র দ্বন্দ্ব ছাড়াই শার্ডিং প্রচার করে, যখন আক্রমনাত্মক কৌশল দ্বন্দ্বের সমাধান করে। উচ্চ আক্রমনাত্মকতা সম্ভাব্য যোগাযোগ খরচ মেমরি পদচিহ্ন কমাতে পারে.
- মৌলিক প্রচার। এটি শ্রেণিবিন্যাসের মধ্যে প্রচারের সর্বনিম্ন কৌশল, যা কোনও বিরোধের সমাধান করে না এবং পরিবর্তে সমস্ত অপারেন্ড এবং ফলাফলের মধ্যে সামঞ্জস্যপূর্ণ অক্ষগুলিকে প্রচার করে।

এই অনুক্রমটিকে লুপগুলির জন্য নেস্টেড হিসাবে ব্যাখ্যা করা যেতে পারে। উদাহরণস্বরূপ, প্রতিটি ব্যবহারকারীর অগ্রাধিকারের জন্য, একটি সম্পূর্ণ অপ-অগ্রাধিকার প্রচার প্রয়োগ করা হয়।
অপারেশন শার্ডিং নিয়ম
শার্ডিং নিয়ম প্রতিটি ক্রিয়াকলাপের একটি বিমূর্ততা প্রবর্তন করে যা নির্দিষ্ট অপারেশনের ধরন এবং তাদের বৈশিষ্ট্যগুলি সম্পর্কে যুক্তি ছাড়াই অপারেন্ড থেকে ফলাফল বা অপারেন্ড জুড়ে শার্ডিংগুলি প্রচার করার জন্য প্রয়োজনীয় তথ্য সহ প্রকৃত প্রচার অ্যালগরিদম সরবরাহ করে। এটি মূলত অপ-নির্দিষ্ট যুক্তিটিকে ফ্যাক্টরিং করছে এবং কেবলমাত্র প্রচারের উদ্দেশ্যে সমস্ত ওপিএসের জন্য একটি ভাগ করা উপস্থাপনা (ডেটা স্ট্রাকচার) সরবরাহ করছে। এর সহজতম আকারে, এটি কেবল এই ফাংশন সরবরাহ করে:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
নিয়মটি আমাদের কেবলমাত্র একবার জেনেরিক উপায়ে প্রচারের অ্যালগরিদম লেখার অনুমতি দেয় যা এই ডেটা স্ট্রাকচারের উপর ভিত্তি করে তৈরি করা হয় ( OpShardingRule ), অনেকগুলি ওপিএস জুড়ে একই ধরণের কোডের টুকরোগুলি প্রতিলিপি করার পরিবর্তে, অপ্সের জুড়ে বাগ বা অসঙ্গতিপূর্ণ আচরণের সম্ভাবনা ব্যাপকভাবে হ্রাস করে।
আসুন ম্যাটমুল উদাহরণে ফিরে যাই।
একটি এনকোডিং যা প্রচারের সময় প্রয়োজনীয় তথ্যগুলিকে আবদ্ধ করে, অর্থাত্, মাত্রাগুলির মধ্যে সম্পর্কগুলি আইনসাম স্বরলিপি আকারে লেখা যেতে পারে:
(i, k), (k, j) -> (i, j)
এই এনকোডিংয়ে, প্রতিটি মাত্রা একটি একক ফ্যাক্টারে ম্যাপ করা হয়।
প্রচার কীভাবে এই ম্যাপিংটি ব্যবহার করে: যদি কোনও অক্ষ/ফলাফলের একটি মাত্রা যদি কোনও অক্ষের সাথে সংযুক্ত থাকে তবে প্রচার এই ম্যাপিংয়ে সেই মাত্রার ফ্যাক্টরটি সন্ধান করবে এবং একই ফ্যাক্টরের সাথে তাদের নিজ নিজ মাত্রার সাথে অন্যান্য অপারেন্ডস/ফলাফলগুলি শার্ড করবে - এবং (প্রতিলিপি সম্পর্কে পূর্বের আলোচনার সাপেক্ষে) যা সম্ভবত অন্য অপারেন্ডস/ফলাফলগুলিও প্রতিলিপি করে না সেই অক্ষ বরাবর।
যৌগিক কারণগুলি: পুনর্নির্মাণের জন্য নিয়ম বাড়ানো
অনেকগুলি অপ্সে, যেমন, ম্যাটমুল, আমাদের কেবলমাত্র প্রতিটি মাত্রা একটি একক ফ্যাক্টরের সাথে মানচিত্র করতে হবে। তবে এটি পুনর্নির্মাণের পক্ষে যথেষ্ট নয়।
নিম্নলিখিত পুনর্নির্মাণ দুটি মাত্রাকে একটিতে মিশিয়ে দেয়:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
এখানে, ইনপুটটির 0 এবং 1 উভয় মাত্রা আউটপুটটির মাত্রা 0 এর সাথে মিলে যায়। বলুন আমরা ইনপুটগুলিতে উপাদানগুলি দিয়ে শুরু করি:
(i,j,k) : i=2, j=4, k=32
আপনি দেখতে পাচ্ছেন যে আমরা যদি আউটপুটটির জন্য একই কারণগুলি ব্যবহার করতে চাই তবে একাধিক কারণগুলি উল্লেখ করার জন্য আমাদের একক মাত্রা প্রয়োজন:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
পুনরায় আকারটি যদি একটি মাত্রা বিভক্ত করে থাকে তবে একই কাজ করা যেতে পারে:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
এখানে,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
এখানে 8 আকারের মাত্রা মূলত 2 এবং 4 টি উপাদানগুলির সমন্বয়ে গঠিত, যার কারণেই আমরা উপাদানগুলি (i,j,k) উপাদানগুলি কল করছি।
এই কারণগুলি এমন ক্ষেত্রেও কাজ করতে পারে যেখানে কোনও সম্পূর্ণ মাত্রা নেই যা কোনও কারণের সাথে মিলে যায়:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
এই উদাহরণটি কেন আমাদের ফ্যাক্টর আকারগুলি সঞ্চয় করতে হবে তাও জোর দেয় - যেহেতু আমরা সহজেই তাদের সংশ্লিষ্ট মাত্রা থেকে অনুমান করতে পারি না।
মূল প্রচার অ্যালগরিদম
কারণ বরাবর শারডিংস প্রচার করুন
শারডিতে, আমাদের কাছে টেনসর, মাত্রা এবং কারণগুলির শ্রেণিবিন্যাস রয়েছে। তারা বিভিন্ন স্তরে ডেটা উপস্থাপন করে। একটি ফ্যাক্টর একটি উপ-মাত্রা। এটি শারডিং প্রচারে ব্যবহৃত একটি অভ্যন্তরীণ শ্রেণিবিন্যাস। প্রতিটি মাত্রা এক বা একাধিক কারণের সাথে মিল থাকতে পারে। মাত্রা এবং ফ্যাক্টরের মধ্যে ম্যাপিংটি OpShardingRule দ্বারা সংজ্ঞায়িত করা হয়।

শারডি মাত্রার পরিবর্তে কারণগুলি বরাবর শারডিং অক্ষগুলি প্রচার করে । এটি করার জন্য, আমাদের নীচের চিত্রটিতে প্রদর্শিত তিনটি পদক্ষেপ রয়েছে:
-
FactorShardingপ্রকল্পDimSharding -
FactorShardingজায়গায় শারডিং অক্ষগুলি প্রচার করুন - আপডেট হওয়া
DimShardingপেতে আপডেটFactorShardingপ্রজেক্ট করুন

কারণগুলির সাথে শারডিং প্রচারের ভিজ্যুয়ালাইজেশন
আমরা নিম্নলিখিত টেবিলটি শারডিং প্রচারের সমস্যা এবং অ্যালগরিদমটি কল্পনা করতে ব্যবহার করব।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি অক্ষ | |
|---|---|---|---|---|
| T0 | ||||
| T1 | ||||
| T2 |
- প্রতিটি কলাম একটি ফ্যাক্টর উপস্থাপন করে। এফ 0 এর অর্থ সূচক 0 সহ ফ্যাক্টর। আমরা কারণগুলি (কলাম) বরাবর শারডিংগুলি প্রচার করি।
- প্রতিটি সারি একটি টেনসর প্রতিনিধিত্ব করে। টি 0 ইনডেক্স 0 সহ টেনসরকে বোঝায়। টেনারগুলি সমস্ত অপারেশন এবং নির্দিষ্ট অপারেশনের জন্য জড়িত ফলাফল। এক সারিতে অক্ষগুলি ওভারল্যাপ করতে পারে না। একটি অক্ষ (বা সাব-অক্ষ) বহুবার একটি টেনসর বিভাজন করতে ব্যবহার করা যায় না। যদি কোনও অক্ষ স্পষ্টভাবে প্রতিলিপি করা হয় তবে আমরা এটি টেনসরকে বিভক্ত করতে ব্যবহার করতে পারি না।
সুতরাং, প্রতিটি কোষ একটি ফ্যাক্টর শারডিং উপস্থাপন করে। আংশিক টেনারগুলিতে একটি ফ্যাক্টর অনুপস্থিত হতে পারে। C = dot(A, B) এর টেবিলটি নীচে রয়েছে। একটি N কোষগুলি বোঝায় যে ফ্যাক্টরটি টেনসরে নেই। উদাহরণস্বরূপ, এফ 2 টি 1 এবং টি 2 এ রয়েছে, তবে টি 0 তে নয়।
C = dot(A, B) | F0 ব্যাচিং ডিম | এফ 1 অ-চুক্তিবদ্ধ ম্লান | এফ 2 অ-চুক্তিবদ্ধ ম্লান | F3 চুক্তি ম্লান | স্পষ্টভাবে প্রতিলিপি অক্ষ |
|---|---|---|---|---|---|
| T0 = a | এন | ||||
| টি 1 = খ | এন | ||||
| টি 2 = গ | এন |
শারডিং অক্ষগুলি সংগ্রহ করুন এবং প্রচার করুন
আমরা প্রচারটি কল্পনা করতে নীচে প্রদর্শিত একটি সাধারণ উদাহরণ ব্যবহার করি।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি অক্ষ | |
|---|---|---|---|---|
| T0 | "একটি" | "চ" | ||
| T1 | "এ", "বি" | "সি", "ডি" | "g" | |
| T2 | "সি", "ই" |
পদক্ষেপ 1। প্রতিটি ফ্যাক্টর (ওরফে (দীর্ঘতম) সামঞ্জস্যপূর্ণ প্রধান শারডিং অক্ষগুলি) বরাবর প্রচার করার জন্য অক্ষগুলি সন্ধান করুন। এই উদাহরণের জন্য, আমরা এফ 0 বরাবর ["a", "b"] প্রচার করি, এফ 1 বরাবর ["c"] প্রচার করি এবং এফ 2 বরাবর কিছুই প্রচার করি না।
পদক্ষেপ 2। নিম্নলিখিত ফলাফলটি পেতে ফ্যাক্টর শারডিংগুলি প্রসারিত করুন।
| F0 | F1 | F2 | স্পষ্টভাবে প্রতিলিপি অক্ষ | |
|---|---|---|---|---|
| T0 | "এ", "বি" | "গ" | "চ" | |
| T1 | "এ", "বি" | "সি", "ডি" | "g" | |
| T2 | "এ", "বি" | "সি", "ই" |
ডেটা ফ্লো অপ্স
উপরের প্রচারের পদক্ষেপের বিবরণটি বেশিরভাগ ওপিএসের ক্ষেত্রে প্রযোজ্য। তবে এমন কিছু ক্ষেত্রে রয়েছে যেখানে একটি শারডিং নিয়ম উপযুক্ত নয়। এই ক্ষেত্রেগুলির জন্য, শারডি ডেটা ফ্লো অপ্সগুলি সংজ্ঞায়িত করে।
কিছু ওপ এক্স এর একটি ডেটা ফ্লো প্রান্তটি উত্সের একটি সেট এবং লক্ষ্যগুলির একটি সেটের মধ্যে একটি সেতু সংজ্ঞায়িত করে, যেমন সমস্ত উত্স এবং লক্ষ্যগুলি একইভাবে বেঁধে রাখা উচিত। এই জাতীয় ওপিগুলির উদাহরণগুলি হ'ল stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp এবং sdy::ManualComputationOp । শেষ পর্যন্ত, যে কোনও ওপি যা শারডেবলটাফ্লোওপিন্টারফেসকে প্রয়োগ করে তা ডেটা ফ্লো ওপি হিসাবে বিবেচিত হয়।
একটি ওপিতে একাধিক ডেটা ফ্লো প্রান্ত থাকতে পারে যা একে অপরের কাছে অরথোগোনাল। যেমন:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
এটি যখন ওপির n ডেটা ফ্লো প্রান্তগুলি রয়েছে: আই-থ ডেটা ফ্লো প্রান্তগুলি x_i , return_value_i উত্সগুলির মধ্যে রয়েছে এবং y_i , pred_arg_i , body_arg_i লক্ষ্য করে।
শারডি সমস্ত উত্স এবং ডেটা প্রবাহ প্রান্তের লক্ষ্যগুলির মধ্যে শার্ডিংসকে প্রচার করবে যেন এটি উত্সগুলি হিসাবে অপারেন্ডস এবং লক্ষ্য হিসাবে উত্সগুলির সাথে নিয়মিত ওপি এবং একটি পরিচয় sdy.op_sharding_rule । এর অর্থ হ'ল ফরোয়ার্ড প্রচার উত্স থেকে লক্ষ্যগুলিতে এবং পিছনের দিকে প্রচার লক্ষ্যগুলি থেকে উত্সগুলিতে।
তাদের মালিকের মাধ্যমে প্রতিটি ডেটা প্রবাহ প্রান্তের উত্স এবং লক্ষ্যগুলি কীভাবে পাবেন এবং কীভাবে প্রান্তের মালিকদের শারডিংগুলি পেতে এবং সেট করবেন তা বর্ণনা করে ব্যবহারকারী দ্বারা বেশ কয়েকটি পদ্ধতি অবশ্যই প্রয়োগ করতে হবে। একজন মালিক হ'ল শারডির প্রচার দ্বারা ব্যবহৃত ডেটা প্রবাহ প্রান্তের ব্যবহারকারী-নির্দিষ্ট লক্ষ্য। ব্যবহারকারী এটি নির্বিচারে চয়ন করতে পারেন তবে এটি স্থির হওয়া দরকার।
উদাহরণস্বরূপ, নীচে সংজ্ঞায়িত custom_op দেওয়া:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
এই কাস্টম_ওপিতে ডেটা প্রবাহের প্রান্তগুলির জন্য দুটি প্রকার রয়েছে: x_i (উত্স) এবং y_i (লক্ষ্য) body_arg_i মধ্যে return_value_i (উত্স) এবং x_i (লক্ষ্য) এবং n n রয়েছে। এই ক্ষেত্রে, প্রান্তের মালিকরা লক্ষ্যগুলির মতোই।

