تکثیر

نمای کلی

انتشار شاردینگ از خرده‌کاری‌های مشخص شده توسط کاربر برای استنباط تقسیم‌بندی نامشخص تانسورها (یا بعد خاص تانسورها) استفاده می‌کند. جریان داده (زنجیره های استفاده-دف) نمودار محاسباتی را در هر دو جهت طی می کند تا زمانی که به یک نقطه ثابت برسد، به عنوان مثال، تقسیم بندی دیگر نمی تواند بدون لغو تصمیمات اشتراک گذاری قبلی تغییر کند.

انتشار را می توان به مراحل تجزیه کرد. هر مرحله شامل بررسی یک عملیات خاص و انتشار بین تانسورها (عملگرها و نتایج)، بر اساس ویژگی های آن عملیات است. با در نظر گرفتن یک matmul به عنوان مثال، بین بعد غیر انقباضی lhs یا rhs به بعد متناظر نتیجه یا بین بعد انقباضی lhs و rhs انتشار می دهیم.

ویژگی‌های یک عملیات ارتباط بین ابعاد متناظر در ورودی و خروجی آن را تعیین می‌کند و می‌تواند به عنوان یک قانون تقسیم عملیاتی انتزاع شود.

بدون حل تعارض، یک مرحله انتشار به سادگی تا آنجا که می تواند منتشر می شود و در عین حال محورهای متضاد را نادیده می گیرد. ما از آن به عنوان (طولانی ترین) محورهای اصلی شاردینگ سازگار یاد می کنیم.

طراحی دقیق

سلسله مراتب حل تعارض

ما چندین استراتژی حل تعارض را در یک سلسله مراتب ترکیب می کنیم:

  1. اولویت های تعریف شده توسط کاربر در Sharding Representation ، توضیح دادیم که چگونه می‌توان اولویت‌ها را به تقسیم‌بندی ابعاد متصل کرد تا امکان پارتیشن‌بندی تدریجی برنامه فراهم شود، به عنوان مثال، انجام موازی‌سازی دسته‌ای -> مگاترون -> تقسیم‌بندی صفر. این با اعمال انتشار در تکرارها به دست می‌آید - در تکرار i همه تقسیم‌بندی‌های ابعادی را که اولویت <=i دارند منتشر می‌کنیم و بقیه را نادیده می‌گیریم. ما همچنین مطمئن می‌شویم که انتشار، اشتراک‌گذاری‌های تعریف‌شده توسط کاربر با اولویت پایین‌تر ( >i ) را لغو نمی‌کند، حتی اگر در تکرارهای قبلی نادیده گرفته شوند.
  2. اولویت های عملیاتی ما بر اساس نوع عملیات، شاردینگ ها را منتشر می کنیم. عملیات "گذر از طریق" (به عنوان مثال، عملیات عنصر عاقلانه و تغییر شکل) بالاترین اولویت را دارند، در حالی که عملیات با تبدیل شکل (مانند نقطه و کاهش) اولویت کمتری دارند.
  3. انتشار تهاجمی شاردینگ ها را با یک استراتژی تهاجمی منتشر کنید. استراتژی اصلی فقط خرده‌کاری‌ها را بدون درگیری منتشر می‌کند، در حالی که استراتژی تهاجمی تضادها را حل می‌کند. تهاجمی بالاتر می تواند ردپای حافظه را به قیمت ارتباطات بالقوه کاهش دهد.
  4. تکثیر اساسی این پایین ترین استراتژی انتشار در سلسله مراتب است، که هیچ حل تعارضی را انجام نمی دهد و در عوض محورهایی را منتشر می کند که بین همه عملوندها و نتایج سازگار هستند.

سلسله مراتب انتشار، نشان دادن 4 پشته، از پایین به بالا، با برچسب های زیر: انتشار پایه، انتشار تهاجمی، اولویت عملیات انتشار، انتشار اولویت کاربر.

این سلسله مراتب را می توان به عنوان حلقه های تو در تو تعبیر کرد. به عنوان مثال، برای هر اولویت کاربر، یک انتشار با اولویت کامل اعمال می شود.

قانون تقسیم عملیات

قانون تقسیم بندی، انتزاعی از هر عملیاتی را معرفی می کند که الگوریتم انتشار واقعی را با اطلاعاتی که برای انتشار تقسیم بندی ها از عملوندها به نتایج یا بین عملوندها بدون نیاز به استدلال در مورد انواع عملیات خاص و ویژگی های آنها نیاز دارد، ارائه می دهد. این اساساً منطق op-specific را فاکتور می‌کند و یک نمایش مشترک (ساختار داده) برای همه عملیات‌ها فقط به منظور انتشار ارائه می‌کند. در ساده ترین شکل خود، فقط این تابع را ارائه می دهد:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

این قانون به ما اجازه می‌دهد تا الگوریتم انتشار را فقط یک بار به روشی عمومی بنویسیم که بر اساس این ساختار داده ( OpShardingRule ) است، به جای اینکه تکه‌های مشابه کد را در بسیاری از عملیات‌ها تکرار کنیم، و احتمال اشکالات یا رفتار ناسازگار در بین عملیات‌ها را به شدت کاهش دهیم.

بیایید به مثال ماتمول برگردیم.

رمزگذاری که اطلاعات مورد نیاز در حین انتشار، یعنی روابط بین ابعاد را در بر می گیرد، می تواند به شکل نماد einsum نوشته شود:

(i, k), (k, j) -> (i, j)

در این رمزگذاری، هر بعد به یک عامل منفرد نگاشت می شود.

چگونه انتشار از این نگاشت استفاده می کند: اگر بعد یک عملوند/نتیجه در امتداد یک محور تقسیم شود، انتشار عامل آن بعد را در این نگاشت جستجو می کند، و سایر عملوندها/نتایج را در امتداد بعد مربوطه خود با همان فاکتور خرد می کند - و (با توجه به بحث قبلی در مورد همانندسازی) به طور بالقوه همچنین عملوندهای دیگر را در امتداد آن فاکتور/نتایج آن محور تکرار می کند.

عوامل مرکب: گسترش قاعده برای تغییر شکل

در بسیاری از عملیات ها، به عنوان مثال، matmul، ما فقط نیاز داریم که هر بعد را به یک عامل منفرد نگاشت کنیم. با این حال، برای تغییر شکل کافی نیست.

شکل زیر دو بعد را در یک بعد ادغام می کند:

%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

در اینجا هر دو بعد 0 و 1 ورودی با بعد 0 خروجی مطابقت دارند. فرض کنید با دادن فاکتورهایی به ورودی شروع می کنیم:

(i,j,k) : i=2, j=4, k=32

می بینید که اگر بخواهیم از عوامل یکسانی برای خروجی استفاده کنیم، برای ارجاع چند عامل به یک بعد واحد نیاز داریم:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

همین کار را می توان انجام داد اگر تغییر شکل یک بعد را تقسیم کند:

%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>

اینجا،

((ij), k) -> (i,j,k) : i=2, j=4, k=32

بعد اندازه 8 در اینجا اساساً از عوامل 2 و 4 تشکیل شده است، به همین دلیل است که ما فاکتورها را فاکتور (i,j,k) می نامیم.

این عوامل همچنین می توانند با مواردی که هیچ بعد کاملی که با یکی از عوامل مطابقت دارد وجود ندارد کار کند:

%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

این مثال همچنین تاکید می کند که چرا باید اندازه فاکتورها را ذخیره کنیم - زیرا نمی توانیم به راحتی آنها را از ابعاد مربوطه استنتاج کنیم.

الگوریتم انتشار هسته

تکه تکه ها را در طول فاکتورها منتشر کنید

در شاردی سلسله مراتب تانسورها، ابعاد و فاکتورها را داریم. آنها داده ها را در سطوح مختلف نشان می دهند. یک عامل یک بعد فرعی است. این یک سلسله مراتب داخلی است که در انتشار به اشتراک گذاری استفاده می شود. هر بعد ممکن است با یک یا چند عامل مطابقت داشته باشد. نگاشت بین بعد و عامل توسط OpShardingRule تعریف می شود.

طرحواره الگوریتم انتشار Shardy را نشان می دهد.

Shardy محورهای شاردینگ را در امتداد فاکتورها به جای ابعاد منتشر می کند . برای انجام این کار، مانند شکل زیر سه مرحله داریم:

  1. پروژه DimSharding به FactorSharding
  2. محورهای شاردینگ را در فضای FactorSharding منتشر کنید
  3. برای دریافت DimSharding به روز شده FactorSharding طراحی کنید

طرحواره ای که انتشار شاردینگ را در FactorSharding و DimSharding نشان می دهد.

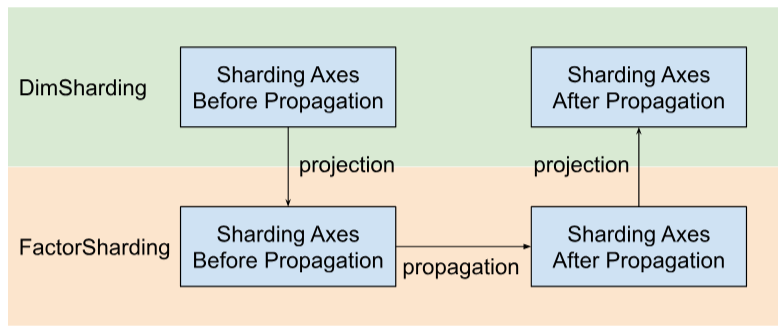
تجسم انتشار شاردینگ در امتداد عوامل

ما از جدول زیر برای تجسم مسئله و الگوریتم انتشار شاردینگ استفاده خواهیم کرد.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0
T1
T2
  • هر ستون نشان دهنده یک عامل است. F0 به معنای عامل با شاخص 0 است. ما تکه تکه ها را در طول فاکتورها (ستون ها) منتشر می کنیم.
  • هر ردیف نشان دهنده یک تانسور است. T0 به تانسور با شاخص 0 اشاره دارد. تانسورها همه عملوندها و نتایج مربوط به یک عملیات خاص هستند. محورها در یک ردیف نمی توانند همپوشانی داشته باشند. یک محور (یا محور فرعی) نمی تواند برای تقسیم یک تانسور چندین بار استفاده شود. اگر یک محور صریحاً تکرار شود، نمی‌توانیم از آن برای پارتیشن بندی تانسور استفاده کنیم.

بنابراین، هر سلول نشان دهنده یک اشتراک فاکتور است. یک عامل ممکن است در تانسورهای جزئی وجود نداشته باشد. جدول C = dot(A, B) در زیر آمده است. سلول های حاوی N نشان می دهد که فاکتور در تانسور نیست. به عنوان مثال، F2 در T1 و T2 است، اما در T0 نیست.

C = dot(A, B) F0 دسته ای کم نور نور غیر انقباضی F1 F2 کم نور غیر انقباضی کم نور انقباض F3 محورهای صراحتاً تکرار شده
T0 = ​​A ن
T1 = B ن
T2 = C ن

محورهای شاردینگ را جمع آوری و منتشر کنید

ما از مثال ساده ای که در زیر نشان داده شده است برای تجسم انتشار استفاده می کنیم.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "الف" "ف"
T1 "الف"، "ب" "ج"، "د" "g"
T2 "ج"، "ه"

مرحله 1. محورهایی را برای انتشار در امتداد هر عامل پیدا کنید (با نام مستعار (طولانی ترین) محورهای اصلی شاردینگ سازگار). برای این مثال، ["a", "b"] را در امتداد F0، ["c"] را در امتداد F1، و هیچ چیز را در امتداد F2 منتشر نمی کنیم.

مرحله 2. تقسیم بندی فاکتورها را برای به دست آوردن نتیجه زیر گسترش دهید.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "الف"، "ب" "ج" "ف"
T1 "الف"، "ب" "ج"، "د" "g"
T2 "الف"، "ب" "ج"، "ه"

عملیات جریان داده

شرح مرحله انتشار بالا برای اکثر عملیات ها اعمال می شود. با این حال، مواردی وجود دارد که قانون اشتراک گذاری مناسب نیست. برای آن موارد، Shardy عملیات جریان داده را تعریف می کند.

لبه جریان داده برخی از عملیات X، پلی را بین مجموعه‌ای از منابع و مجموعه‌ای از اهداف تعریف می‌کند، به گونه‌ای که همه منابع و اهداف باید به یک شکل تقسیم شوند. نمونه هایی از این عملیات عبارتند از stablehlo::OptimizationBarrierOp ، stablehlo::WhileOp ، stablehlo::CaseOp و همچنین sdy::ManualComputationOp . در نهایت، هر عملیاتی که ShardableDataFlowOpInterface را پیاده سازی کند، عملیات جریان داده در نظر گرفته می شود.

یک عملیات می تواند دارای لبه های جریان داده های متعددی باشد که متعامد با یکدیگر هستند. به عنوان مثال:

    y_0, ..., y_n = while (x_0, ..., x_n)
                    ((pred_arg_0,... , pred_arg_n) { ... })
                    ((body_arg_0,..., body_arg_n) {
                    ...
                    return return_value_0, ..., return_value_n
                    })

این درحالی است که op دارای n لبه جریان داده است: iمین لبه جریان داده بین منابع x_i ، return_value_i و اهداف y_i ، pred_arg_i ، body_arg_i است.

Shardy تقسیم‌بندی‌ها را بین همه منابع و اهداف یک لبه جریان داده منتشر می‌کند، گویی یک عملیات معمولی با منابع به‌عنوان عملوند و اهداف به‌عنوان نتایج، و یک هویت sdy.op_sharding_rule . این بدان معناست که انتشار رو به جلو از منبع به هدف و انتشار به عقب از هدف به منبع است.

چندین روش باید توسط کاربر پیاده سازی شود که نحوه دریافت منابع و اهداف هر لبه جریان داده از طریق صاحب آنها و همچنین نحوه دریافت و تنظیم تقسیم بندی صاحبان لبه ها را شرح می دهد. مالک یک هدف مشخص شده توسط کاربر از لبه جریان داده است که توسط انتشار Shardy استفاده می شود. کاربر می تواند آن را خودسرانه انتخاب کند اما باید ثابت باشد.

به عنوان مثال، با توجه به custom_op تعریف شده در زیر: 

  y_1, ..., y_n = custom_op (x_1, ..., x_n)
                  ((body_arg_1,..., body_arg_n) {
                    ...
                    return return_value_1, ..., return_value_n
                  })

این custom_op دو نوع برای لبه‌های جریان داده دارد: n یال هر کدام بین return_value_i (منبع) و y_i (هدف‌ها) و n یال بین x_i (منبع) و body_arg_i (هدف‌ها). در این حالت، صاحبان لبه همان اهداف هستند.

،

نمای کلی

انتشار شاردینگ از خرده‌کاری‌های مشخص شده توسط کاربر برای استنباط تقسیم‌بندی نامشخص تانسورها (یا بعد خاص تانسورها) استفاده می‌کند. جریان داده (زنجیره های استفاده-دف) نمودار محاسباتی را در هر دو جهت طی می کند تا زمانی که به یک نقطه ثابت برسد، به عنوان مثال، تقسیم بندی دیگر نمی تواند بدون لغو تصمیمات اشتراک گذاری قبلی تغییر کند.

انتشار را می توان به مراحل تجزیه کرد. هر مرحله شامل بررسی یک عملیات خاص و انتشار بین تانسورها (عملگرها و نتایج)، بر اساس ویژگی های آن عملیات است. با در نظر گرفتن یک matmul به عنوان مثال، بین بعد غیر انقباضی lhs یا rhs به بعد متناظر نتیجه یا بین بعد انقباضی lhs و rhs انتشار می دهیم.

ویژگی‌های یک عملیات ارتباط بین ابعاد متناظر در ورودی و خروجی آن را تعیین می‌کند و می‌تواند به عنوان یک قانون تقسیم عملیاتی انتزاع شود.

بدون حل تعارض، یک مرحله انتشار به سادگی تا آنجا که می تواند منتشر می شود و در عین حال محورهای متضاد را نادیده می گیرد. ما از آن به عنوان (طولانی ترین) محورهای اصلی شاردینگ سازگار یاد می کنیم.

طراحی دقیق

سلسله مراتب حل تعارض

ما چندین استراتژی حل تعارض را در یک سلسله مراتب ترکیب می کنیم:

  1. اولویت های تعریف شده توسط کاربر در Sharding Representation ، توضیح دادیم که چگونه می‌توان اولویت‌ها را به تقسیم‌بندی ابعاد متصل کرد تا امکان پارتیشن‌بندی تدریجی برنامه فراهم شود، به عنوان مثال، انجام موازی‌سازی دسته‌ای -> مگاترون -> تقسیم‌بندی صفر. این با اعمال انتشار در تکرارها به دست می‌آید - در تکرار i همه تقسیم‌بندی‌های ابعادی را که اولویت <=i دارند منتشر می‌کنیم و بقیه را نادیده می‌گیریم. ما همچنین مطمئن می‌شویم که انتشار، اشتراک‌گذاری‌های تعریف‌شده توسط کاربر با اولویت پایین‌تر ( >i ) را لغو نمی‌کند، حتی اگر در تکرارهای قبلی نادیده گرفته شوند.
  2. اولویت های عملیاتی ما بر اساس نوع عملیات، شاردینگ ها را منتشر می کنیم. عملیات "گذر از طریق" (به عنوان مثال، عملیات عنصر عاقلانه و تغییر شکل) بالاترین اولویت را دارند، در حالی که عملیات با تبدیل شکل (مانند نقطه و کاهش) اولویت کمتری دارند.
  3. انتشار تهاجمی شاردینگ ها را با یک استراتژی تهاجمی منتشر کنید. استراتژی اصلی فقط خرده‌کاری‌ها را بدون درگیری منتشر می‌کند، در حالی که استراتژی تهاجمی تضادها را حل می‌کند. تهاجمی بالاتر می تواند ردپای حافظه را به قیمت ارتباطات بالقوه کاهش دهد.
  4. تکثیر اساسی این پایین ترین استراتژی انتشار در سلسله مراتب است، که هیچ حل تعارضی را انجام نمی دهد و در عوض محورهایی را منتشر می کند که بین همه عملوندها و نتایج سازگار هستند.

سلسله مراتب انتشار، نشان دادن 4 پشته، از پایین به بالا، با برچسب های زیر: انتشار پایه، انتشار تهاجمی، اولویت عملیات انتشار، انتشار اولویت کاربر.

این سلسله مراتب را می توان به عنوان حلقه های تو در تو تعبیر کرد. به عنوان مثال، برای هر اولویت کاربر، یک انتشار با اولویت کامل اعمال می شود.

قانون تقسیم عملیات

قانون تقسیم بندی، انتزاعی از هر عملیاتی را معرفی می کند که الگوریتم انتشار واقعی را با اطلاعاتی که برای انتشار تقسیم بندی ها از عملوندها به نتایج یا بین عملوندها بدون نیاز به استدلال در مورد انواع عملیات خاص و ویژگی های آنها نیاز دارد، ارائه می دهد. این اساساً منطق op-specific را فاکتور می‌کند و یک نمایش مشترک (ساختار داده) برای همه عملیات‌ها فقط به منظور انتشار ارائه می‌کند. در ساده ترین شکل خود، فقط این تابع را ارائه می دهد:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

این قانون به ما اجازه می‌دهد تا الگوریتم انتشار را فقط یک بار به روشی عمومی بنویسیم که بر اساس این ساختار داده ( OpShardingRule ) است، به جای اینکه تکه‌های مشابه کد را در بسیاری از عملیات‌ها تکرار کنیم، و احتمال اشکالات یا رفتار ناسازگار در بین عملیات‌ها را به شدت کاهش دهیم.

بیایید به مثال ماتمول برگردیم.

رمزگذاری که اطلاعات مورد نیاز در حین انتشار، یعنی روابط بین ابعاد را در بر می گیرد، می تواند به شکل نماد einsum نوشته شود:

(i, k), (k, j) -> (i, j)

در این رمزگذاری، هر بعد به یک عامل منفرد نگاشت می شود.

چگونه انتشار از این نگاشت استفاده می کند: اگر بعد یک عملوند/نتیجه در امتداد یک محور تقسیم شود، انتشار عامل آن بعد را در این نگاشت جستجو می کند، و سایر عملوندها/نتایج را در امتداد بعد مربوطه خود با همان فاکتور خرد می کند - و (با توجه به بحث قبلی در مورد همانندسازی) به طور بالقوه همچنین عملوندهای دیگر را در امتداد آن فاکتور/نتایج آن محور تکرار می کند.

عوامل مرکب: گسترش قاعده برای تغییر شکل

در بسیاری از عملیات ها، به عنوان مثال، matmul، ما فقط نیاز داریم که هر بعد را به یک عامل منفرد نگاشت کنیم. با این حال، برای تغییر شکل کافی نیست.

شکل زیر دو بعد را در یک بعد ادغام می کند:

%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

در اینجا هر دو بعد 0 و 1 ورودی با بعد 0 خروجی مطابقت دارند. فرض کنید با دادن فاکتورهایی به ورودی شروع می کنیم:

(i,j,k) : i=2, j=4, k=32

می بینید که اگر بخواهیم از عوامل یکسانی برای خروجی استفاده کنیم، برای ارجاع چند عامل به یک بعد واحد نیاز داریم:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

همین کار را می توان انجام داد اگر تغییر شکل یک بعد را تقسیم کند:

%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>

اینجا،

((ij), k) -> (i,j,k) : i=2, j=4, k=32

بعد اندازه 8 در اینجا اساساً از عوامل 2 و 4 تشکیل شده است، به همین دلیل است که ما فاکتورها را فاکتور (i,j,k) می نامیم.

این عوامل همچنین می توانند با مواردی که هیچ بعد کاملی که با یکی از عوامل مطابقت دارد وجود ندارد کار کند:

%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

این مثال همچنین تاکید می کند که چرا باید اندازه فاکتورها را ذخیره کنیم - زیرا نمی توانیم به راحتی آنها را از ابعاد مربوطه استنتاج کنیم.

الگوریتم انتشار هسته

تکه تکه ها را در طول فاکتورها منتشر کنید

در شاردی سلسله مراتب تانسورها، ابعاد و فاکتورها را داریم. آنها داده ها را در سطوح مختلف نشان می دهند. یک عامل یک بعد فرعی است. این یک سلسله مراتب داخلی است که در انتشار به اشتراک گذاری استفاده می شود. هر بعد ممکن است با یک یا چند عامل مطابقت داشته باشد. نگاشت بین بعد و عامل توسط OpShardingRule تعریف می شود.

طرحواره الگوریتم انتشار Shardy را نشان می دهد.

Shardy محورهای شاردینگ را در امتداد فاکتورها به جای ابعاد منتشر می کند . برای انجام این کار، مانند شکل زیر سه مرحله داریم:

  1. پروژه DimSharding به FactorSharding
  2. محورهای شاردینگ را در فضای FactorSharding منتشر کنید
  3. برای دریافت DimSharding به روز شده FactorSharding طراحی کنید

طرحواره ای که انتشار شاردینگ را در FactorSharding و DimSharding نشان می دهد.

تجسم انتشار شاردینگ در امتداد عوامل

ما از جدول زیر برای تجسم مسئله و الگوریتم انتشار شاردینگ استفاده خواهیم کرد.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0
T1
T2
  • هر ستون نشان دهنده یک عامل است. F0 به معنای عامل با شاخص 0 است. ما تکه تکه ها را در طول فاکتورها (ستون ها) منتشر می کنیم.
  • هر ردیف نشان دهنده یک تانسور است. T0 به تانسور با شاخص 0 اشاره دارد. تانسورها همه عملوندها و نتایج مربوط به یک عملیات خاص هستند. محورها در یک ردیف نمی توانند همپوشانی داشته باشند. یک محور (یا محور فرعی) نمی تواند برای تقسیم یک تانسور چندین بار استفاده شود. اگر یک محور صریحاً تکرار شود، نمی‌توانیم از آن برای پارتیشن بندی تانسور استفاده کنیم.

بنابراین، هر سلول نشان دهنده یک اشتراک فاکتور است. یک عامل ممکن است در تانسورهای جزئی وجود نداشته باشد. جدول C = dot(A, B) در زیر آمده است. سلول های حاوی N نشان می دهد که فاکتور در تانسور نیست. به عنوان مثال، F2 در T1 و T2 است، اما در T0 نیست.

C = dot(A, B) F0 کم نور دسته ای F1 نور غیر انقباضی F2 کم نور غیر انقباضی کم نور انقباض F3 محورهای صراحتاً تکرار شده
T0 = ​​A ن
T1 = B ن
T2 = C ن

محورهای شاردینگ را جمع آوری و منتشر کنید

ما از مثال ساده ای که در زیر نشان داده شده است برای تجسم انتشار استفاده می کنیم.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "الف" "ف"
T1 "الف"، "ب" "ج"، "د" "g"
T2 "ج"، "ه"

مرحله 1. محورهایی را برای انتشار در امتداد هر عامل پیدا کنید (با نام مستعار (طولانی ترین) محورهای اصلی شاردینگ سازگار). برای این مثال، ["a", "b"] را در امتداد F0، ["c"] را در امتداد F1، و هیچ چیز را در امتداد F2 منتشر نمی کنیم.

مرحله 2. تقسیم بندی فاکتورها را برای به دست آوردن نتیجه زیر گسترش دهید.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "الف"، "ب" "ج" "ف"
T1 "الف"، "ب" "ج"، "د" "g"
T2 "الف"، "ب" "ج"، "ه"

عملیات جریان داده

شرح مرحله انتشار بالا برای اکثر عملیات ها اعمال می شود. با این حال، مواردی وجود دارد که قانون اشتراک گذاری مناسب نیست. برای آن موارد، Shardy عملیات جریان داده را تعریف می کند.

لبه جریان داده برخی از عملیات X، پلی را بین مجموعه‌ای از منابع و مجموعه‌ای از اهداف تعریف می‌کند، به گونه‌ای که همه منابع و اهداف باید به یک شکل تقسیم شوند. نمونه هایی از این عملیات عبارتند از stablehlo::OptimizationBarrierOp ، stablehlo::WhileOp ، stablehlo::CaseOp و همچنین sdy::ManualComputationOp . در نهایت، هر عملیاتی که ShardableDataFlowOpInterface را پیاده سازی کند، عملیات جریان داده در نظر گرفته می شود.

یک عملیات می تواند دارای لبه های جریان داده های متعددی باشد که متعامد با یکدیگر هستند. به عنوان مثال:

    y_0, ..., y_n = while (x_0, ..., x_n)
                    ((pred_arg_0,... , pred_arg_n) { ... })
                    ((body_arg_0,..., body_arg_n) {
                    ...
                    return return_value_0, ..., return_value_n
                    })

این درحالی است که op دارای n لبه جریان داده است: iمین لبه جریان داده بین منابع x_i ، return_value_i و اهداف y_i ، pred_arg_i ، body_arg_i است.

Shardy تقسیم‌بندی‌ها را بین همه منابع و اهداف یک لبه جریان داده منتشر می‌کند، گویی یک عملیات معمولی با منابع به‌عنوان عملوند و اهداف به‌عنوان نتایج، و یک هویت sdy.op_sharding_rule . این بدان معناست که انتشار رو به جلو از منبع به هدف و انتشار به عقب از هدف به منبع است.

چندین روش باید توسط کاربر پیاده سازی شود که نحوه دریافت منابع و اهداف هر لبه جریان داده از طریق صاحب آنها و همچنین نحوه دریافت و تنظیم تقسیم بندی صاحبان لبه ها را شرح می دهد. مالک یک هدف مشخص شده توسط کاربر از لبه جریان داده است که توسط انتشار Shardy استفاده می شود. کاربر می تواند آن را خودسرانه انتخاب کند اما باید ثابت باشد.

به عنوان مثال، با توجه به custom_op تعریف شده در زیر: 

  y_1, ..., y_n = custom_op (x_1, ..., x_n)
                  ((body_arg_1,..., body_arg_n) {
                    ...
                    return return_value_1, ..., return_value_n
                  })

این custom_op دو نوع برای لبه‌های جریان داده دارد: n یال هر کدام بین return_value_i (منبع) و y_i (هدف‌ها) و n یال بین x_i (منبع) و body_arg_i (هدف‌ها). در این حالت، صاحبان لبه همان اهداف هستند.

،

نمای کلی

انتشار شاردینگ از خرده‌کاری‌های مشخص شده توسط کاربر برای استنباط تقسیم‌بندی نامشخص تانسورها (یا بعد خاص تانسورها) استفاده می‌کند. جریان داده (زنجیره های استفاده-دف) نمودار محاسباتی را در هر دو جهت طی می کند تا زمانی که به یک نقطه ثابت برسد، به عنوان مثال، تقسیم بندی دیگر نمی تواند بدون لغو تصمیمات اشتراک گذاری قبلی تغییر کند.

انتشار را می توان به مراحل تجزیه کرد. هر مرحله شامل بررسی یک عملیات خاص و انتشار بین تانسورها (عملگرها و نتایج)، بر اساس ویژگی های آن عملیات است. با در نظر گرفتن یک matmul به عنوان مثال، بین بعد غیر انقباضی lhs یا rhs به بعد متناظر نتیجه یا بین بعد انقباضی lhs و rhs انتشار می دهیم.

ویژگی‌های یک عملیات ارتباط بین ابعاد متناظر در ورودی و خروجی آن را تعیین می‌کند و می‌تواند به عنوان یک قانون تقسیم عملیاتی انتزاع شود.

بدون حل تعارض، یک مرحله انتشار به سادگی تا آنجا که می تواند منتشر می شود و در عین حال محورهای متضاد را نادیده می گیرد. ما از آن به عنوان (طولانی ترین) محورهای اصلی شاردینگ سازگار یاد می کنیم.

طراحی دقیق

سلسله مراتب حل تعارض

ما چندین استراتژی حل تعارض را در یک سلسله مراتب ترکیب می کنیم:

  1. اولویت های تعریف شده توسط کاربر در Sharding Representation ، توضیح دادیم که چگونه می‌توان اولویت‌ها را به تقسیم‌بندی ابعاد متصل کرد تا امکان پارتیشن‌بندی تدریجی برنامه فراهم شود، به عنوان مثال، انجام موازی‌سازی دسته‌ای -> مگاترون -> تقسیم‌بندی صفر. این با اعمال انتشار در تکرارها به دست می‌آید - در تکرار i همه تقسیم‌بندی‌های ابعادی را که اولویت <=i دارند منتشر می‌کنیم و بقیه را نادیده می‌گیریم. ما همچنین مطمئن می‌شویم که انتشار، اشتراک‌گذاری‌های تعریف‌شده توسط کاربر با اولویت پایین‌تر ( >i ) را لغو نمی‌کند، حتی اگر در تکرارهای قبلی نادیده گرفته شوند.
  2. اولویت های عملیاتی ما بر اساس نوع عملیات، شاردینگ ها را منتشر می کنیم. عملیات "گذر از طریق" (به عنوان مثال، عملیات عنصر عاقلانه و تغییر شکل) بالاترین اولویت را دارند، در حالی که عملیات با تبدیل شکل (مانند نقطه و کاهش) اولویت کمتری دارند.
  3. انتشار تهاجمی شاردینگ ها را با یک استراتژی تهاجمی منتشر کنید. استراتژی اصلی فقط خرده‌کاری‌ها را بدون درگیری منتشر می‌کند، در حالی که استراتژی تهاجمی تضادها را حل می‌کند. تهاجمی بالاتر می تواند ردپای حافظه را به قیمت ارتباطات بالقوه کاهش دهد.
  4. تکثیر اساسی این پایین ترین استراتژی انتشار در سلسله مراتب است، که هیچ حل تعارضی را انجام نمی دهد و در عوض محورهایی را منتشر می کند که بین همه عملوندها و نتایج سازگار هستند.

سلسله مراتب انتشار، نشان دادن 4 پشته، از پایین به بالا، با برچسب های زیر: انتشار پایه، انتشار تهاجمی، اولویت عملیات انتشار، انتشار اولویت کاربر.

این سلسله مراتب را می توان به عنوان حلقه های تو در تو تعبیر کرد. به عنوان مثال، برای هر اولویت کاربر، یک انتشار با اولویت کامل اعمال می شود.

قانون تقسیم عملیات

قانون تقسیم بندی، انتزاعی از هر عملیاتی را معرفی می کند که الگوریتم انتشار واقعی را با اطلاعاتی که برای انتشار تقسیم بندی ها از عملوندها به نتایج یا بین عملوندها بدون نیاز به استدلال در مورد انواع عملیات خاص و ویژگی های آنها نیاز دارد، ارائه می دهد. این اساساً منطق op-specific را فاکتور می‌کند و یک نمایش مشترک (ساختار داده) برای همه عملیات‌ها فقط به منظور انتشار ارائه می‌کند. در ساده ترین شکل خود، فقط این تابع را ارائه می دهد:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

این قانون به ما اجازه می‌دهد تا الگوریتم انتشار را فقط یک بار به روشی عمومی بنویسیم که بر اساس این ساختار داده ( OpShardingRule ) است، به جای اینکه تکه‌های مشابه کد را در بسیاری از عملیات‌ها تکرار کنیم، و احتمال اشکالات یا رفتار ناسازگار در بین عملیات‌ها را به شدت کاهش دهیم.

بیایید به مثال ماتمول برگردیم.

رمزگذاری که اطلاعات مورد نیاز در حین انتشار، یعنی روابط بین ابعاد را در بر می گیرد، می تواند به شکل نماد einsum نوشته شود:

(i, k), (k, j) -> (i, j)

در این رمزگذاری، هر بعد به یک عامل منفرد نگاشت می شود.

چگونه انتشار از این نگاشت استفاده می کند: اگر بعد یک عملوند/نتیجه در امتداد یک محور تقسیم شود، انتشار عامل آن بعد را در این نگاشت جستجو می کند، و سایر عملوندها/نتایج را در امتداد بعد مربوطه خود با همان فاکتور خرد می کند - و (با توجه به بحث قبلی در مورد همانندسازی) به طور بالقوه همچنین عملوندهای دیگر را در امتداد آن فاکتور/نتایج آن محور تکرار می کند.

عوامل مرکب: گسترش قاعده برای تغییر شکل

در بسیاری از عملیات ها، به عنوان مثال، matmul، ما فقط نیاز داریم که هر بعد را به یک عامل منفرد نگاشت کنیم. با این حال، برای تغییر شکل کافی نیست.

شکل زیر دو بعد را در یک بعد ادغام می کند:

%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

در اینجا هر دو بعد 0 و 1 ورودی با بعد 0 خروجی مطابقت دارند. فرض کنید با دادن فاکتورهایی به ورودی شروع می کنیم:

(i,j,k) : i=2, j=4, k=32

می بینید که اگر بخواهیم از عوامل یکسانی برای خروجی استفاده کنیم، برای ارجاع چند عامل به یک بعد واحد نیاز داریم:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

همین کار را می توان انجام داد اگر تغییر شکل یک بعد را تقسیم کند:

%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>

اینجا،

((ij), k) -> (i,j,k) : i=2, j=4, k=32

بعد اندازه 8 در اینجا اساساً از عوامل 2 و 4 تشکیل شده است، به همین دلیل است که ما فاکتورها را فاکتور (i,j,k) می نامیم.

این عوامل همچنین می توانند با مواردی که هیچ بعد کاملی که با یکی از عوامل مطابقت دارد وجود ندارد کار کند:

%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

این مثال همچنین تاکید می کند که چرا باید اندازه فاکتورها را ذخیره کنیم - زیرا نمی توانیم به راحتی آنها را از ابعاد مربوطه استنتاج کنیم.

الگوریتم انتشار هسته

تکه تکه ها را در طول فاکتورها منتشر کنید

در شاردی سلسله مراتب تانسورها، ابعاد و فاکتورها را داریم. آنها داده ها را در سطوح مختلف نشان می دهند. یک عامل یک بعد فرعی است. این یک سلسله مراتب داخلی است که در انتشار به اشتراک گذاری استفاده می شود. هر بعد ممکن است با یک یا چند عامل مطابقت داشته باشد. نگاشت بین بعد و عامل توسط OpShardingRule تعریف می شود.

طرحواره الگوریتم انتشار Shardy را نشان می دهد.

Shardy محورهای شاردینگ را در امتداد فاکتورها به جای ابعاد منتشر می کند . برای انجام این کار، مانند شکل زیر سه مرحله داریم:

  1. پروژه DimSharding به FactorSharding
  2. محورهای شاردینگ را در فضای FactorSharding منتشر کنید
  3. برای دریافت DimSharding به روز شده FactorSharding طراحی کنید

طرحواره ای که انتشار شاردینگ را در FactorSharding و DimSharding نشان می دهد.

تجسم انتشار شاردینگ در امتداد عوامل

ما از جدول زیر برای تجسم مسئله و الگوریتم انتشار شاردینگ استفاده خواهیم کرد.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0
T1
T2
  • هر ستون نشان دهنده یک عامل است. F0 به معنای عامل با شاخص 0 است. ما تکه تکه ها را در طول فاکتورها (ستون ها) منتشر می کنیم.
  • هر ردیف نشان دهنده یک تانسور است. T0 به تانسور با شاخص 0 اشاره دارد. تانسورها همه عملوندها و نتایج مربوط به یک عملیات خاص هستند. محورها در یک ردیف نمی توانند همپوشانی داشته باشند. یک محور (یا محور فرعی) نمی تواند برای تقسیم یک تانسور چندین بار استفاده شود. اگر یک محور صریحاً تکرار شود، نمی‌توانیم از آن برای پارتیشن بندی تانسور استفاده کنیم.

بنابراین، هر سلول نشان دهنده یک اشتراک فاکتور است. یک عامل ممکن است در تانسورهای جزئی وجود نداشته باشد. جدول C = dot(A, B) در زیر آمده است. سلول های حاوی N نشان می دهد که فاکتور در تانسور نیست. به عنوان مثال، F2 در T1 و T2 است، اما در T0 نیست.

C = dot(A, B) F0 کم نور دسته ای F1 نور غیر انقباضی F2 کم نور غیر انقباضی کم نور انقباض F3 محورهای صراحتاً تکرار شده
T0 = ​​A ن
T1 = B ن
T2 = C ن

محورهای شاردینگ را جمع آوری و منتشر کنید

ما از مثال ساده ای که در زیر نشان داده شده است برای تجسم انتشار استفاده می کنیم.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "الف" "ف"
T1 "الف"، "ب" "ج"، "د" "g"
T2 "ج"، "ه"

مرحله 1. محورهایی را برای انتشار در امتداد هر عامل پیدا کنید (با نام مستعار (طولانی ترین) محورهای اصلی شاردینگ سازگار). برای این مثال، ["a", "b"] را در امتداد F0، ["c"] را در امتداد F1، و هیچ چیز را در امتداد F2 منتشر نمی کنیم.

مرحله 2. تقسیم بندی فاکتورها را برای به دست آوردن نتیجه زیر گسترش دهید.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "الف"، "ب" "ج" "ف"
T1 "الف"، "ب" "ج"، "د" "g"
T2 "الف"، "ب" "ج"، "ه"

عملیات جریان داده

شرح مرحله انتشار بالا برای اکثر عملیات ها اعمال می شود. با این حال، مواردی وجود دارد که قانون اشتراک گذاری مناسب نیست. برای آن موارد، Shardy عملیات جریان داده را تعریف می کند.

لبه جریان داده برخی از عملیات X، پلی را بین مجموعه‌ای از منابع و مجموعه‌ای از اهداف تعریف می‌کند، به گونه‌ای که همه منابع و اهداف باید به یک شکل تقسیم شوند. نمونه هایی از این عملیات عبارتند از stablehlo::OptimizationBarrierOp ، stablehlo::WhileOp ، stablehlo::CaseOp و همچنین sdy::ManualComputationOp . در نهایت، هر عملیاتی که ShardableDataFlowOpInterface را پیاده سازی کند، عملیات جریان داده در نظر گرفته می شود.

یک عملیات می تواند دارای لبه های جریان داده های متعددی باشد که متعامد با یکدیگر هستند. به عنوان مثال:

    y_0, ..., y_n = while (x_0, ..., x_n)
                    ((pred_arg_0,... , pred_arg_n) { ... })
                    ((body_arg_0,..., body_arg_n) {
                    ...
                    return return_value_0, ..., return_value_n
                    })

این درحالی است که op دارای n لبه جریان داده است: iمین لبه جریان داده بین منابع x_i ، return_value_i و اهداف y_i ، pred_arg_i ، body_arg_i است.

Shardy تقسیم‌بندی‌ها را بین همه منابع و اهداف یک لبه جریان داده منتشر می‌کند، گویی یک عملیات معمولی با منابع به‌عنوان عملوند و اهداف به‌عنوان نتایج، و یک هویت sdy.op_sharding_rule . این بدان معناست که انتشار رو به جلو از منبع به هدف و انتشار به عقب از هدف به منبع است.

چندین روش باید توسط کاربر پیاده سازی شود که نحوه دریافت منابع و اهداف هر لبه جریان داده از طریق صاحب آنها و همچنین نحوه دریافت و تنظیم تقسیم بندی صاحبان لبه ها را شرح می دهد. مالک یک هدف مشخص شده توسط کاربر از لبه جریان داده است که توسط انتشار Shardy استفاده می شود. کاربر می تواند آن را خودسرانه انتخاب کند اما باید ثابت باشد.

به عنوان مثال، با توجه به custom_op تعریف شده در زیر: 

  y_1, ..., y_n = custom_op (x_1, ..., x_n)
                  ((body_arg_1,..., body_arg_n) {
                    ...
                    return return_value_1, ..., return_value_n
                  })

این custom_op دو نوع برای لبه‌های جریان داده دارد: n یال هر کدام بین return_value_i (منبع) و y_i (هدف‌ها) و n یال بین x_i (منبع) و body_arg_i (هدف‌ها). در این حالت، صاحبان لبه همان اهداف هستند.

،

نمای کلی

انتشار شاردینگ از خرده‌کاری‌های مشخص شده توسط کاربر برای استنباط تقسیم‌بندی نامشخص تانسورها (یا بعد خاص تانسورها) استفاده می‌کند. جریان داده (زنجیره های استفاده-دف) نمودار محاسباتی را در هر دو جهت طی می کند تا زمانی که به یک نقطه ثابت برسد، به عنوان مثال، تقسیم بندی دیگر نمی تواند بدون لغو تصمیمات اشتراک گذاری قبلی تغییر کند.

انتشار را می توان به مراحل تجزیه کرد. هر مرحله شامل بررسی یک عملیات خاص و انتشار بین تانسورها (عملگرها و نتایج)، بر اساس ویژگی های آن عملیات است. با در نظر گرفتن یک matmul به عنوان مثال، بین بعد غیر انقباضی lhs یا rhs به بعد متناظر نتیجه یا بین بعد انقباضی lhs و rhs انتشار می دهیم.

ویژگی‌های یک عملیات ارتباط بین ابعاد متناظر در ورودی و خروجی آن را تعیین می‌کند و می‌تواند به عنوان یک قانون تقسیم عملیاتی انتزاع شود.

بدون حل تعارض، یک مرحله انتشار به سادگی تا آنجا که می تواند منتشر می شود و در عین حال محورهای متضاد را نادیده می گیرد. ما از آن به عنوان (طولانی ترین) محورهای اصلی شاردینگ سازگار یاد می کنیم.

طراحی دقیق

سلسله مراتب حل تعارض

ما چندین استراتژی حل تعارض را در یک سلسله مراتب ترکیب می کنیم:

  1. اولویت های تعریف شده توسط کاربر در Sharding Representation ، توضیح دادیم که چگونه می‌توان اولویت‌ها را به تقسیم‌بندی ابعاد متصل کرد تا امکان پارتیشن‌بندی تدریجی برنامه فراهم شود، به عنوان مثال، انجام موازی‌سازی دسته‌ای -> مگاترون -> تقسیم‌بندی صفر. این با اعمال انتشار در تکرارها به دست می‌آید - در تکرار i همه تقسیم‌بندی‌های ابعادی را که اولویت <=i دارند منتشر می‌کنیم و بقیه را نادیده می‌گیریم. ما همچنین مطمئن می‌شویم که انتشار، اشتراک‌گذاری‌های تعریف‌شده توسط کاربر با اولویت پایین‌تر ( >i ) را لغو نمی‌کند، حتی اگر در تکرارهای قبلی نادیده گرفته شوند.
  2. اولویت های عملیاتی ما بر اساس نوع عملیات، شاردینگ ها را منتشر می کنیم. عملیات "گذر از طریق" (به عنوان مثال، عملیات عنصر عاقلانه و تغییر شکل) بالاترین اولویت را دارند، در حالی که عملیات با تبدیل شکل (مانند نقطه و کاهش) اولویت کمتری دارند.
  3. انتشار تهاجمی شاردینگ ها را با یک استراتژی تهاجمی منتشر کنید. استراتژی اصلی فقط خرده‌کاری‌ها را بدون درگیری منتشر می‌کند، در حالی که استراتژی تهاجمی تضادها را حل می‌کند. تهاجمی بالاتر می تواند ردپای حافظه را به قیمت ارتباطات بالقوه کاهش دهد.
  4. تکثیر اساسی این پایین ترین استراتژی انتشار در سلسله مراتب است، که هیچ حل تعارضی را انجام نمی دهد و در عوض محورهایی را منتشر می کند که بین همه عملوندها و نتایج سازگار هستند.

سلسله مراتب انتشار، نشان دادن 4 پشته، از پایین به بالا، با برچسب های زیر: انتشار پایه، انتشار تهاجمی، اولویت عملیات انتشار، انتشار اولویت کاربر.

این سلسله مراتب را می توان به عنوان حلقه های تو در تو تعبیر کرد. به عنوان مثال، برای هر اولویت کاربر، یک انتشار با اولویت کامل اعمال می شود.

قانون تقسیم عملیات

قانون تقسیم بندی، انتزاعی از هر عملیاتی را معرفی می کند که الگوریتم انتشار واقعی را با اطلاعاتی که برای انتشار تقسیم بندی ها از عملوندها به نتایج یا بین عملوندها بدون نیاز به استدلال در مورد انواع عملیات خاص و ویژگی های آنها نیاز دارد، ارائه می دهد. این اساساً منطق op-specific را فاکتور می‌کند و یک نمایش مشترک (ساختار داده) برای همه عملیات‌ها فقط به منظور انتشار ارائه می‌کند. در ساده ترین شکل خود، فقط این تابع را ارائه می دهد:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

این قانون به ما اجازه می‌دهد تا الگوریتم انتشار را فقط یک بار به روشی عمومی بنویسیم که بر اساس این ساختار داده ( OpShardingRule ) است، به جای اینکه تکه‌های مشابه کد را در بسیاری از عملیات‌ها تکرار کنیم، و احتمال اشکالات یا رفتار ناسازگار در بین عملیات‌ها را به شدت کاهش دهیم.

بیایید به مثال ماتمول برگردیم.

رمزگذاری که اطلاعات مورد نیاز در حین انتشار، یعنی روابط بین ابعاد را در بر می گیرد، می تواند به شکل نماد einsum نوشته شود:

(i, k), (k, j) -> (i, j)

در این رمزگذاری، هر بعد به یک عامل منفرد نگاشت می شود.

چگونه انتشار از این نقشه برداری استفاده می کند: اگر ابعادی از یک عمل/نتیجه در امتداد یک محور به هم ریخته شود ، تکثیر عامل آن بعد را در این نقشه برداری جستجو می کند ، و سایر عملکردها/نتایج را در طول بعد مربوطه با همان عامل - و (با توجه به بحث قبلی در مورد تکثیر) به طور بالقوه نیز تکرار می کند که سایر عملکردها/نتایج حاصل از آن وجود ندارد که عامل آن را ندارد.

عوامل مرکب: گسترش قانون برای تغییر شکل

در بسیاری از OPS ، به عنوان مثال ، Matmul ، ما فقط باید هر بعد را به یک عامل واحد ترسیم کنیم. با این حال ، برای تغییر شکل کافی نیست.

تغییر شکل زیر دو بعد را در یک ادغام می کند:

%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

در اینجا ، هر دو بعد 0 و 1 ورودی با ابعاد 0 خروجی مطابقت دارند. بگویید ما با ارائه عوامل به ورودی شروع می کنیم:

(i,j,k) : i=2, j=4, k=32

می بینید که اگر می خواهیم از همان عوامل برای خروجی استفاده کنیم ، برای مرجع چندین عامل به یک بعد واحد نیاز داریم:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

اگر تغییر شکل یک بعد تقسیم شود ، می توان همین کار را انجام داد:

%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>

اینجا،

((ij), k) -> (i,j,k) : i=2, j=4, k=32

ابعاد اندازه 8 در اینجا اساساً از عوامل 2 و 4 تشکیل شده است ، به همین دلیل ما عوامل عوامل (i,j,k) را می نامیم.

این عوامل همچنین می توانند با مواردی کار کنند که هیچ ابعادی کامل با یکی از عوامل وجود نداشته باشد:

%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

این مثال همچنین تأکید می کند که چرا ما نیاز به ذخیره اندازه فاکتور داریم - از آنجا که نمی توانیم به راحتی آنها را از ابعاد مربوطه استنباط کنیم.

الگوریتم انتشار اصلی

در امتداد عوامل قابل پخش است

در Shardy ، ما سلسله مراتب تانسورس ، ابعاد و عوامل را داریم. آنها داده ها را در سطوح مختلف نشان می دهند. یک عامل یک ابعاد زیر است. این یک سلسله مراتب داخلی است که در انتشار آن استفاده می شود. هر بعد ممکن است با یک یا چند عامل مطابقت داشته باشد. نقشه برداری بین ابعاد و فاکتور توسط OpShardingRule تعریف شده است.

طرحواره ای که الگوریتم انتشار Shardy را نشان می دهد.

Shardy به جای ابعاد ، محورهای Sharding را در امتداد عوامل پخش می کند . برای انجام این کار ، ما سه مرحله داریم که در شکل زیر نشان داده شده است:

  1. DimSharding Project to FactorSharding
  2. محورهای Sharding را در فضای FactorSharding پخش کنید
  3. FactorSharding به روز شده را برای به دست آوردن DimSharding به روز شده پروژه کنید

طرحواره ای که نشان دهنده انتشار در سراسر فاکتور و کمرنگ شدن است.

تجسم انتشار Sharding در امتداد عوامل

ما از جدول زیر برای تجسم مشکل انتشار Sharding و الگوریتم استفاده خواهیم کرد.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0
T1
T2
  • هر ستون یک عامل را نشان می دهد. F0 به معنای عاملی با شاخص 0 است. ما در امتداد عوامل (ستون ها) Shardings را پخش می کنیم.
  • هر سطر یک تانسور را نشان می دهد. T0 به تانسور با شاخص 0 اشاره دارد. تنش ها همه عملیات و نتایج مربوط به یک عملیات خاص هستند. محورهای یک ردیف نمی توانند با هم همپوشانی داشته باشند. یک محور (یا زیر محور) نمی تواند بارها برای تقسیم یک تانسور استفاده شود. اگر یک محور به صراحت تکرار شود ، ما نمی توانیم از آن برای تقسیم تانسور استفاده کنیم.

بنابراین ، هر سلول نمایانگر یک فاکتور است. یک عامل می تواند در تنسورهای جزئی وجود داشته باشد. جدول C = dot(A, B) در زیر آمده است. سلولهای حاوی N حاکی از آن است که این عامل در تانسور نیست. به عنوان مثال ، F2 در T1 و T2 است ، اما در T0 نیست.

C = dot(A, B) F0 Batching Dim F1 DIM DIM F2 DIM DIM F3 پیمانکاری کم نور محورهای صراحتاً تکرار شده
T0 = ​​a ن
T1 = b ن
T2 = C ن

محورهای Sharding را جمع آوری و پخش کنید

ما برای تجسم انتشار از یک مثال ساده در زیر استفاده می کنیم.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "الف" "F"
T1 "A" ، "B" "C" ، "D" "g"
T2 "ج" ، "E"

مرحله 1. محورها را برای پخش در امتداد هر عامل (با نام مستعار (طولانی ترین) محورهای اصلی سازگار) پیدا کنید. برای این مثال ، ما ["a", "b"] را در امتداد F0 پخش می کنیم ، ["c"] را در امتداد F1 پخش می کنیم و هیچ چیزی را در امتداد F2 پخش نمی کنیم.

مرحله 2. برای به دست آوردن نتیجه زیر ، قطعه های فاکتور را گسترش دهید.

F0 F1 F2 محورهای صراحتاً تکرار شده
T0 "A" ، "B" "ج" "F"
T1 "A" ، "B" "C" ، "D" "g"
T2 "A" ، "B" "ج" ، "E"

عملیات جریان داده

توضیحات مرحله انتشار فوق در مورد اکثر OPS اعمال می شود. با این حال ، مواردی وجود دارد که یک قانون شاری مناسب نیست. برای این موارد ، Shardy گزینه های جریان داده را تعریف می کند.

لبه جریان داده برخی از OP X پلی بین مجموعه ای از منابع و مجموعه ای از اهداف را تعریف می کند ، به گونه ای که باید همه منابع و اهداف به همان روش خرد شوند. نمونه هایی از چنین گزینه هایی stablehlo::OptimizationBarrierOp ، stablehlo::WhileOp ، stablehlo::CaseOp و همچنین sdy::ManualComputationOp است. در نهایت ، هر OP که ShardableDataFlowOpinterface را پیاده سازی کند ، یک جریان داده در نظر گرفته می شود.

یک عملیات می تواند دارای لبه های جریان داده های متعددی باشد که متعامد با یکدیگر هستند. به عنوان مثال:

    y_0, ..., y_n = while (x_0, ..., x_n)
                    ((pred_arg_0,... , pred_arg_n) { ... })
                    ((body_arg_0,..., body_arg_n) {
                    ...
                    return return_value_0, ..., return_value_n
                    })

این در حالی است که OP دارای لبه های جریان داده n است: لبه های جریان داده I-Th بین منابع x_i ، return_value_i و هدف قرار دادن y_i ، pred_arg_i ، body_arg_i است.

Shardy بین همه منابع و اهداف یک لبه جریان داده را پخش می کند ، گویی که این یک OP معمولی با منابع به عنوان عمل و اهداف به عنوان نتایج و یک هویت sdy.op_sharding_rule است. این بدان معناست که انتشار رو به جلو از منابع به اهداف و انتشار عقب از اهداف به منابع است.

روش های مختلفی باید توسط کاربر توضیح داده شود که چگونه می توان منابع و اهداف هر لبه جریان داده را از طریق صاحب خود دریافت کرد ، و همچنین نحوه به دست آوردن و تنظیم قسمت های صاحبان Edge. یک مالک یک هدف مشخص شده توسط کاربر از لبه جریان داده است که توسط انتشار Shardy استفاده می شود. کاربر می تواند آن را خودسرانه انتخاب کند اما باید ثابت باشد.

به عنوان مثال ، با توجه به custom_op تعریف شده در زیر: 

  y_1, ..., y_n = custom_op (x_1, ..., x_n)
                  ((body_arg_1,..., body_arg_n) {
                    ...
                    return return_value_1, ..., return_value_n
                  })

این Custom_op برای لبه های جریان داده دو نوع دارد: n هر یک بین return_value_i (منابع) و y_i (اهداف) و لبه های n بین x_i (منابع) و body_arg_i (اهداف). در این حالت ، صاحبان Edge همان اهداف هستند.