繁殖

概要

シャーディング伝播では、ユーザー指定のシャーディングを使用して、テンソルの未指定のシャーディング（またはテンソルの特定のディメンション）を推測します。固定ポイントに到達するまで、計算グラフのデータフローを（使用定義チェーンで）両方向に走査します。つまり、以前のシャーディング決定を元に戻さないとシャーディングを変更できなくなります。

伝播はステップに分解できます。各ステップでは、特定のオペレーションを調べ、そのオペレーションの特性に基づいてテンソル（オペランドと結果）間で伝播します。matmul を例に取ると、lhs または rhs の収縮しないディメンションから結果の対応するディメンションに、または lhs と rhs の収縮ディメンション間で伝播します。

オペレーションの特性により、入力と出力の対応するディメンション間の接続が決まります。これは、オペレーションごとのシャーディング ルールとして抽象化できます。

競合解決がないと、伝播ステップは競合する軸を無視して、可能な限り多くのデータを伝播します。これを（最も長い）互換性のあるメジャー シャーディング軸と呼びます。

詳細な設計

競合解決の階層

複数の競合解決戦略を階層で構成します。

1. ユーザー定義の優先度。シャーディング表現では、バッチ並列処理 -> Megatron -> ZeRO シャーディングなど、プログラムの増分パーティショニングを可能にするために、ディメンション シャーディングに優先度を割り当てる方法について説明しました。これは、反復処理で伝播を適用することで実現されます。反復処理 i では、優先度 <=i のすべてのディメンション シャーディングを伝播し、他のすべてのディメンション シャーディングを無視します。また、以前のイテレーションで無視された場合でも、優先度が低い（>i）ユーザー定義シャーディングが伝播によってオーバーライドされないようにします。
2. オペレーションベースの優先度。シャーディングは、オペレーション タイプに基づいて伝播されます。「パススルー」オペレーション（要素ごとのオペレーションや再シェイプなど）は優先度が最も高く、シェイプ変換のオペレーション（ドットや reduce など）は優先度が低くなります。
3. 積極的な伝播。積極的な戦略でシャーディングを伝播します。基本戦略では、競合のないシャーディングのみが伝播されますが、積極的な戦略では競合が解決されます。アグレッシブさを高めると、通信の可能性を犠牲にしてメモリ フットプリントを削減できます。
4. 基本的な伝播。これは、階層内で最も低い伝播戦略です。競合解決は行わず、すべてのオペランドと結果で互換性のある軸を伝播します。

この階層は、ネストされた for ループと解釈できます。たとえば、ユーザーの優先度ごとに、完全なオペレーション優先度の伝播が適用されます。

オペレーション シャーディング ルール

シャーディング ルールは、特定のオペレーション タイプとその属性を推論することなく、オペランドから結果に、またはオペランド間でシャーディングを伝播するために必要な情報を実際の伝播アルゴリズムに提供する、すべてのオペレーションの抽象化を導入します。これは基本的に、オペレーション固有のロジックをファクトリ分離し、伝播のみを目的としてすべてのオペレーションに共有表現（データ構造）を提供します。最も単純な形式では、次の関数のみを提供します。

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

このルールにより、多くのオペレーションに類似したコードを複製するのではなく、このデータ構造（OpShardingRule）に基づく汎用的な方法で伝播アルゴリズムを 1 回だけ記述できるため、オペレーション間でのバグや動作の不整合の可能性を大幅に減らすことができます。

matmul の例に戻りましょう。

伝播中に必要な情報（ディメンション間の関係）をカプセル化するエンコードは、einsum 表記の形式で記述できます。

(i, k), (k, j) -> (i, j)

このエンコードでは、すべてのディメンションが 1 つの要因にマッピングされます。

このマッピングが伝播でどのように使用されるか: オペランドまたは結果のディメンションが軸に沿ってシャーディングされている場合、伝播は、このマッピングでそのディメンションの係数を検索し、同じ係数でそれぞれのディメンションに沿って他のオペランドまたは結果をシャーディングします。また、（前述のレプリケーションに関する説明に従って）その軸に沿ってその係数を持たない他のオペランドまたは結果もレプリケートする可能性があります。

複合要因: 再構成のルールを拡張する

matmul などの多くのオペレーションでは、各ディメンションを単一の係数にマッピングするだけで済みます。ただし、この方法では、再構成には不十分です。

次のリシェイプは、2 つのディメンションを 1 つに統合します。

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

ここで、入力の 0 番目と 1 番目のディメンションはどちらも出力の 0 番目のディメンションに対応しています。まず、入力に要素を指定します。

(i,j,k) : i=2, j=4, k=32

出力に同じ要因を使用する場合は、複数の要因を参照する単一のディメンションが必要になります。

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

再構成でディメンションが分割された場合も、同じことができます。

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

ここでのサイズ 8 のディメンションは、基本的に要素 2 と 4 で構成されているため、要素（i、j、k）要素と呼ばれます。

これらの要素は、いずれかの要素に対応する完全なディメンションがない場合にも使用できます。

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

この例は、対応するディメンションから係数サイズを簡単に推測できないため、係数サイズを保存する必要がある理由も示しています。

コア伝播アルゴリズム

ファクタに沿ってシャーディングを伝播する

Shardy には、テンソル、ディメンション、ファクタの階層があります。これらは異なるレベルのデータを表します。要素はサブディメンションです。これは、シャーディング伝播で使用される内部階層です。各ディメンションは 1 つ以上の要因に対応しています。ディメンションとファクタのマッピングは、OpShardingRule によって定義されます。

Shardy は、ディメンションではなくファクタに沿ってシャーディング軸を伝播します。そのためには、次の図に示す 3 つのステップが必要です。

1. プロジェクトの DimSharding を FactorSharding に移行する
2. FactorSharding の空間でシャーディング軸を伝播する
3. 更新された FactorSharding を投影して、更新された DimSharding を取得する

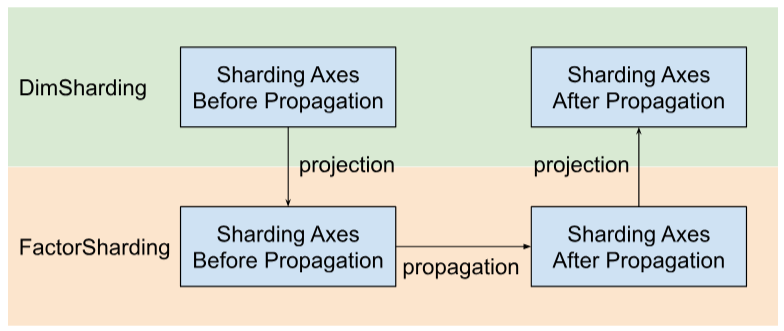
ファクタに沿ったシャーディング伝播の可視化

シャーディング伝播の問題とアルゴリズムを可視化するために、次の表を使用します。

	F0	F1	F2	明示的に複製された軸
T0
T1
T2

• 各列は 1 つの要因を表します。F0 は、インデックス 0 の係数を意味します。シャーディングはファクタ（列）に沿って伝播されます。
• 各行はテンソルを表します。T0 はインデックス 0 のテンソルを指します。テンソルは、特定のオペレーションに関連するすべてのオペランドと結果です。行内の軸は重複できません。1 つのテンソルを複数回パーティショニングするために、軸（またはサブ軸）を使用できません。軸が明示的に複製されている場合、その軸を使用してテンソルをパーティショニングすることはできません。

したがって、各セルはファクタ シャーディングを表します。部分テンソルには要素が欠落している場合があります。C = dot(A, B) の表を以下に示します。N を含むセルは、係数がテンソル内にないことを意味します。たとえば、F2 は T1 と T2 にありますが、T0 にはありません。

C = dot(A, B)	F0 バッチ処理による明るさの低下	F1 非収縮ディメンション	F2 非収縮調光	F3 契約による明るさの低下	明示的に複製された軸
T0 = A			N
T1 = B		N
T2 = C				N

シャーディング軸を収集して伝播する

以下に示す単純な例を使用して、伝播を可視化します。

	F0	F1	F2	明示的に複製された軸
T0	「a」		「f」
T1	「a」、「b」	「c」、「d」	"g"
T2		「c」、「e」

ステップ 1. 各要素に沿って伝播する軸（互換性のある（最長の）メジャー シャーディング軸）を見つけます。この例では、F0 に沿って ["a", "b"] を伝播し、F1 に沿って ["c"] を伝播し、F2 に沿って何も伝播しません。

ステップ 2. ファクタ シャーディングを展開すると、次の結果が得られます。

	F0	F1	F2	明示的に複製された軸
T0	「a」、「b」	"c"	「f」
T1	「a」、「b」	「c」、「d」	"g"
T2	"a"、"b"	「c」、「e」