更改的生效时间

概览

分片传播使用用户指定的分片来推断张量（或张量的特定维度）的未指定分片。它会在两个方向上遍历计算图的数据流（使用-定义链），直到达到固定点，即在不撤消之前的分片决策的情况下，分片无法再更改。

传播可以分解为步骤。每个步骤都涉及查看特定运算，并根据该运算的特性在张量（运算数和结果）之间传播。以矩阵乘法为例，我们会在左侧或右侧的非收缩维度之间传播到结果的相应维度，或者在左侧和右侧的收缩维度之间传播。

操作的特性决定了其输入和输出中对应维度之间的关联，并且可以抽象为按操作的分片规则。

如果不进行冲突解决，传播步骤只会尽可能传播，同时忽略冲突的轴；我们将其称为（最长）兼容的主要分片轴。

详细设计

冲突解决层次结构

我们在层次结构中组合使用多种冲突解决策略：

1. 用户定义的优先级。在分片表示法中，我们介绍了如何将优先级附加到维度分片，以允许对程序进行增量分区，例如执行批处理并行 -> Megatron -> ZERO 分片。为此，我们会在迭代中应用传播 - 在迭代 i 中，我们会传播优先级为 <=i 的所有维度分片，并忽略所有其他维度分片。我们还确保传播不会覆盖优先级较低（>i）的用户定义分片，即使在之前的迭代中忽略了这些分片也是如此。
2. 基于操作的优先级。我们会根据操作类型传播分片。“透传”操作（例如按元素操作和重塑）的优先级最高，而具有形状转换的操作（例如点积和求和）的优先级较低。
3. 积极传播。使用激进策略传播分片。 基本策略仅会传播没有冲突的分片，而激进策略会解决冲突。更高的侵略性可以降低内存占用量，但会导致潜在的通信开销。
4. 基本传播。这是层次结构中最低级别的传播策略，不会执行任何冲突解决，而是传播所有运算数和结果之间兼容的轴。

此层次结构可以解释为嵌套的 for 循环。例如，对于每个用户优先级，系统都会应用完整的操作优先级传播。

操作分片规则

分片规则引入了对每项操作的抽象，可为实际传播算法提供从运算数传播到结果或跨运算数传播分片等所需的信息，而无需推理特定操作类型及其属性。这在本质上是提取特定于操作的逻辑，并为所有操作提供共享表示法（数据结构），仅出于传播目的。形式最简单的 ViewModel 仅提供以下函数：

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

借助此规则，我们只需基于此数据结构（OpShardingRule）以通用方式编写一次传播算法，而无需在许多操作中复制类似的代码段，从而大大降低了操作之间出现 bug 或行为不一致的可能性。

我们回到 matmul 示例。

用于封装传播过程中所需信息（即维度之间的关系）的编码可以采用 einsum 表示法编写：

(i, k), (k, j) -> (i, j)

在此编码中，每个维度都会映射到一个因子。

传播如何使用此映射：如果运算数/结果的某个维度沿某个轴进行分片，传播将在此映射中查找该维度的系数，并使用相同的系数沿其各自的维度分片其他运算数/结果，并且（根据前面关于复制的讨论）可能还会沿该轴复制不具有该系数的其他运算数/结果。

复合因子：扩展重塑规则

在许多运算（例如矩阵乘法）中，我们只需将每个维度映射到一个因子即可。但是，对于重塑，这还不够。

以下 reshape 会将两个维度合并为一个：

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

在这里，输入的维度 0 和 1 都对应于输出的维度 0。假设我们先为输入提供因子：

(i,j,k) : i=2, j=4, k=32

您可以看到，如果我们想对输出使用相同的因素，则需要使用单个维度来引用多个因素：

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

如果 reshape 会拆分某个维度，也可以执行相同的操作：

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

这里大小为 8 的维度本质上由因子 2 和 4 组成，因此我们将因子 (i,j,k) 称为因子。

这些因素也适用于没有与其中一个因素对应的完整维度的情况：

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

此示例还强调了我们需要存储因子尺寸的原因，因为我们无法轻松地从相应尺寸推断出这些尺寸。

核心传播算法

沿着分桶因子传播分桶

在 Shardy 中，我们有张量、维度和因子的层次结构。它们表示不同层级的数据。因素是子维度。这是分片传播中使用的内部层次结构。每个维度都可能对应于一个或多个因素。维度与因子之间的映射由 OpShardingRule 定义。

Shardy 会沿着因子（而非维度）传播分片轴。为此，我们需要完成以下三个步骤，如下图所示

1. 将项目 DimSharding 更改为 FactorSharding
2. 在 FactorSharding 的空间中传播分片轴
3. 投影更新后的 FactorSharding 以获取更新后的 DimSharding

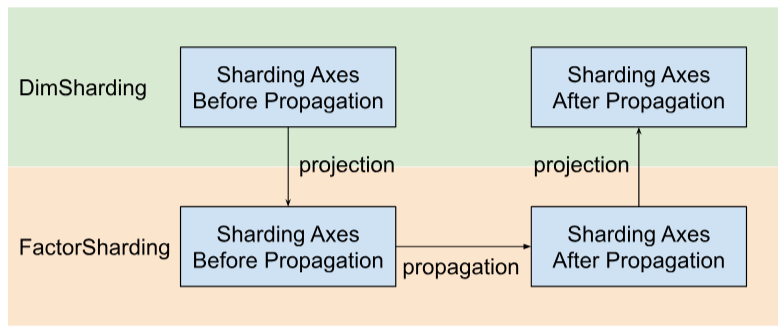
直观呈现因子沿分片传播的情况

我们将使用下表直观呈现分片传播问题和算法。

	F0	F1	F2	显式复制的轴
T0
T1
T2

• 每列代表一个因子。F0 表示索引为 0 的系数。我们会沿因子（列）传播分片。
• 每行代表一个张量。T0 表示索引为 0 的张量。张量是指特定运算涉及的所有运算数和运算结果。同一行中的轴不能重叠。一个轴（或子轴）不能多次用于对一个张量进行分区。如果某个轴被明确复制，我们将无法使用该轴对张量进行分区。

因此，每个单元格都代表一个因子分片。部分张量中可能会缺少因子。下表显示了 C = dot(A, B)。包含 N 的单元格表示该因子不在张量中。例如，F2 位于 T1 和 T2 中，但不位于 T0 中。

C = dot(A, B)	F0 批处理调光	F1 非收缩调光	F2 非收缩暗淡	F3 收缩暗淡	显式复制的轴
T0 = A			否
T1 = B		否
T2 = C				否

收集和传播分片轴

我们将使用下面的简单示例直观地展示传播过程。

	F0	F1	F2	显式复制的轴
T0	"a"		“f”
T1	“a”“b”	“c”“d”	"g"
T2		“c”“e”

第 1 步. 查找要沿每个因素传播的轴（也称为（最长）兼容的主要分片轴）。在此示例中，我们沿 F0 传播 ["a", "b"]，沿 F1 传播 ["c"]，并沿 F2 传播无内容。

第 2 步：展开因子分片，即可得到以下结果。

	F0	F1	F2	显式复制的轴
T0	“a”“b”	"c"	“f”
T1	“a”“b”	“c”“d”	"g"
T2	"a"、"b"	“c”“e”