Propagacja

Omówienie

Propagowanie podziału na fragmenty wykorzystuje określone przez użytkownika podziały na fragmenty, aby wywnioskować nieokreślone podziały na fragmenty tensorów (lub określony wymiar tensorów). Przechodzi przez przepływ danych (łańcuchy use-def) w grafice obliczeń w obu kierunkach, aż do osiągnięcia punktu stałego, czyli momentu, w którym podział nie może się już zmienić bez cofnięcia poprzednich decyzji dotyczących podziału.

Propagację można podzielić na etapy. Każdy krok polega na rozpatrywaniu konkretnej operacji i przekazywanie informacji między tensorami (operandami i wynikami) w zależności od charakterystyki tej operacji. Na przykład w przypadku funkcji matmul propagujemy wymiar niekurczący się z elementu lhs lub rhs do odpowiadającego wymiaru wyniku albo z wymiaru kurczącego się z elementu lhs i rhs.

Charakterystyka operacji określa związek między odpowiednimi wymiarami na wejściu i wyjściu, a także może być zastąpiona regułą podziału na operację.

Bez rozwiązywania konfliktów propagacja odbywałaby się w największym możliwym zakresie, ignorując sprzeczne osie. Nazywamy to (najdłuższymi) zgodnymi głównymi osiami podziału.

Szczegółowy projekt

Hierarchia rozwiązywania konfliktów

W hierarchii tworzymy wiele strategii rozwiązywania konfliktów:

1. Priorytety zdefiniowane przez użytkownika. W sekcji Reprezentacja podziału na części opisaliśmy, jak można przypisywać priorytety do podziałów wymiarów, aby umożliwić stopniowe dzielenie programu na części, np. stosowanie równoległości zbiorczej –> megatron –> podział ZeRO. Osiągamy to, stosując propagowanie w iteracjach – w iteracji i propagujemy wszystkie podziały wymiarów, które mają priorytet <=i, i ignorujemy wszystkie pozostałe. Dbamy też o to, aby propagowanie nie zastępowało podziału zdefiniowanego przez użytkownika o niższym priorytecie (>i), nawet jeśli jest on ignorowany w poprzednich iteracjach.
2. Priorytety operacyjne. Rozdzielanie jest propagowane na podstawie typu operacji. Operacje „przepuszczania” (np. operacje element po elemencie i przekształcanie kształtu) mają najwyższy priorytet, a operacje z przekształceniem kształtu (np. dot i reduce) – niższy.
3. Agresywna propagacja. Rozpowszechniaj podziały za pomocą strategii agresywnej. Strategia podstawowa rozpowszechnia tylko podziały bez konfliktów, a strategia agresywna rozwiązuje konflikty. Większa agresywność może zmniejszyć zapotrzebowanie na pamięć kosztem potencjalnej komunikacji.
4. Podstawowa propagacja. Jest to strategia propagowania o najniższej pozycji w hierarchii, która nie rozwiązuje konfliktów, lecz propaguje osie, które są zgodne ze wszystkimi operandami i wynikami.

Tę hierarchię można interpretować jako zagnieżdżone pętle for. Na przykład w przypadku każdego priorytetu użytkownika stosuje się pełną propagację priorytetu op.

Reguła podziału operacji

Reguła podziału wprowadza abstrakcję każdej operacji, która dostarcza rzeczywistemu algorytmowi propagacji informacji potrzebnych do propagowania podziału od operandów do wyników lub między operandami itp., bez konieczności rozważania konkretnych typów operacji i ich atrybutów. Polega to zasadniczo na wyodrębnieniu logiki związanej z konkretną operacją i zapewnieniu wspólnej reprezentacji (struktury danych) dla wszystkich operacji tylko na potrzeby propagowania. W najprostszej formie platforma ta umożliwia tylko to:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

Ta reguła pozwala nam napisać algorytm propagacji tylko raz w ogólnym formacie, który opiera się na tej strukturze danych (OpShardingRule), zamiast powielać podobne fragmenty kodu w wielu operacjach, co znacznie zmniejsza prawdopodobieństwo wystąpienia błędów lub niespójności w operacjach.

Wróćmy do przykładu matmul.

Kodowanie, które zawiera informacje potrzebne podczas propagacji, czyli relacje między wymiarami, może być zapisane w formie zapisu einsum:

(i, k), (k, j) -> (i, j)

W tym kodowaniu każdy wymiar jest mapowany na jeden czynnik.

Jak propagacja używa tego mapowania: jeśli wymiar operandu lub wyniku jest dzielony wzdłuż osi, propagacja wyszuka współczynnik tej osi w tym mapowaniu i podzieli inne operandy/wyniki wzdłuż ich wymiaru z tym samym współczynnikiem – a także (zgodnie z wcześniejszą dyskusją na temat replikowania) potencjalnie też powieli inne operandy/wyniki, które nie mają tego współczynnika wzdłuż tej osi.

Czynniki złożone: rozszerzenie reguły dotyczącej zmian kształtu

W wielu operacjach, np. matmul, wystarczy zmapować każdy wymiar na jeden czynnik. Nie wystarczy jednak do zmiany kształtu.

Ta operacja zmiany kształtu łączy 2 wymiary w jeden:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

W tym przypadku oba wymiary 0 i 1 na wejściu odpowiadają wymiarowi 0 na wyjściu. Załóżmy, że zaczynamy od podania czynników wejściowych:

(i,j,k) : i=2, j=4, k=32

Jeśli chcemy, aby w wyniku były używane te same czynniki, potrzebujemy 1 wymiaru, który będzie się odwoływał do wielu czynników:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

To samo można zrobić, jeśli przekształcenie ma podzielić wymiar:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

Wymiar o wielkości 8 składa się głównie z czynników 2 i 4, dlatego nazywamy je czynnikami (i,j,k).

Te czynniki mogą też działać w przypadkach, gdy nie ma pełnego wymiaru odpowiadającego jednemu z tych czynników:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Ten przykład pokazuje też, dlaczego musimy przechowywać rozmiary czynników, ponieważ nie możemy ich łatwo wywnioskować z odpowiednich wymiarów.

Główny algorytm propagacji

Propagowanie podziału na czynniki

W Shardy mamy hierarchię tensorów, wymiarów i czynników. Przedstawiają one dane na różnych poziomach. Czynnik to podwymiar. Jest to wewnętrzna hierarchia używana w propagacji podziału. Każdy wymiar może odpowiadać co najmniej 1 czynnikowi. Mapowanie wymiaru i czynnika jest zdefiniowane przez regułę OpShardingRule.

Shardy rozpowszechnia osie podziału wzdłuż czynników zamiast wymiarów. Aby to zrobić, wykonaj 3 podstawowe czynności przedstawione na rysunku poniżej.

1. Przejście z projektu DimSharding na FactorSharding
2. Propagowanie osi podziału w przestrzeni czynników
3. Przeprowadź projekcję zaktualizowanego modułu FactorSharding, aby uzyskać zaktualizowany moduł DimSharding.

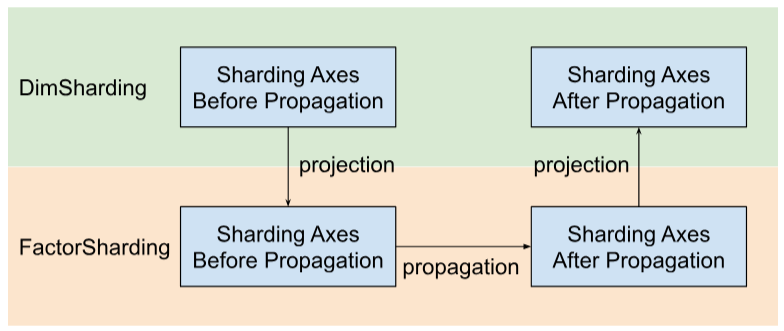
Wizualizacja propagacji podziału na fragmenty w zależności od czynników

Aby zilustrować problem i algorytm propagacji fragmentacji, użyjemy tej tabeli.

	F0	F1	F2	Wyraźnie powielane osie
T0
T1
T2

• Każda kolumna odpowiada jednemu czynnikowi. F0 oznacza czynnik o indeksie 0. Rozprowadzimy dzielenie na czynniki (kolumny).
• Każdy wiersz reprezentuje tensor. T0 odnosi się do tensora o indeksie 0. Tensory to wszystkie operandy i wyniki zaangażowane w konkretną operację. Osie w wierszu nie mogą się pokrywać. Osi (ani podosi) nie można używać do wielokrotnego dzielenia jednego tensora. Jeśli oś jest wyraźnie powielana, nie możemy jej użyć do podziału tensora.

W związku z tym każda komórka reprezentuje podział czynnika. W przypadku tensorów częściowych może brakować czynnika. Tabela C = dot(A, B) znajduje się poniżej. Komórki zawierające wartość N wskazują, że czynnik nie występuje w tensorze. Na przykład F2 znajduje się w T1 i T2, ale nie w T0.

C = dot(A, B)	F0 Grupowanie przyciemnienia	F1 Niewypełnianie umowy	F2 Niezmieniająca się jasność	F3 Contracting dim	Wyraźnie powielane osie
T0 = A			N
T1 = B		N
T2 = C				N

Pobieranie i rozpowszechnianie osi podziału

Aby zilustrować propagację, posłużymy się prostym przykładem przedstawionym poniżej.

	F0	F1	F2	Wyraźnie powielane osie
T0	„a”		„f”
T1	„a”, „b”	„c”, „d”	„g”
T2		„c”, „e”.

Krok 1. Znajdź osie, które mają być propagowane wzdłuż każdego czynnika (czyli zgodne z głównymi osiami podziału). W tym przykładzie propagujemy wartość ["a", "b"] wzdłuż krawędzi F0, propagujemy wartość ["c"] wzdłuż krawędzi F1, a nic nie propagujemy wzdłuż krawędzi F2.

Krok 2. Rozwiń podziały czynników, aby uzyskać ten wynik.

	F0	F1	F2	Wyraźnie powielane osie
T0	"a", "b"	„c”	„f”
T1	„a”, „b”	„c”, „d”	„g”
T2	„a”, „b”	„c”, „e”.