इस पेज का अनुवाद Cloud Translation API से किया गया है.

प्रजनन
संग्रह की मदद से व्यवस्थित रहें अपनी प्राथमिकताओं के आधार पर, कॉन्टेंट को सेव करें और कैटगरी में बांटें.

खास जानकारी

शीयरिंग प्रॉपेगेशन, उपयोगकर्ता की बताई गई शीयरिंग का इस्तेमाल करके, टेंसर (या टेंसर के किसी खास डाइमेंशन) की बताई गई शीयरिंग का अनुमान लगाता है. यह कैलकुलेशन ग्राफ़ के डेटा फ़्लो (इस्तेमाल-परिभाषा चेन) को दोनों दिशाओं में तब तक ट्रैवर्स करता है, जब तक कि कोई तय बिंदु नहीं मिल जाता. इसका मतलब है कि शर्डिंग के पिछले फ़ैसलों को पहले से वापस लिए बिना, शर्डिंग में बदलाव नहीं किया जा सकता.

प्रॉपेगेशन को चरणों में बांटा जा सकता है. हर चरण में, किसी खास ऑपरेशन को देखा जाता है और उस ऑपरेशन की विशेषताओं के आधार पर, टेंसर (ऑपरेंड और नतीजे) के बीच प्रॉपेगेट किया जाता है. उदाहरण के लिए, matmul का इस्तेमाल करके, हम lhs या rhs के नॉन-कंट्रैक्टिंग डाइमेंशन से, नतीजे के उसी डाइमेंशन में या lhs और rhs के कंट्रैक्टिंग डाइमेंशन के बीच प्रॉपेगेट करेंगे.

किसी ऑपरेशन की विशेषताएं, उसके इनपुट और आउटपुट में मौजूद मिलते-जुलते डाइमेंशन के बीच के कनेक्शन को तय करती हैं. साथ ही, इन्हें ऑपरेशन के हिसाब से शर्डिंग नियम के तौर पर अलग किया जा सकता है.

विरोध को हल किए बिना, प्रॉपर्टी के प्रॉपेगेशन का चरण, ज़्यादा से ज़्यादा डेटा को प्रॉपेगेट करेगा. ऐसा करते समय, वह विरोध करने वाले ऐक्सिस को अनदेखा करेगा. हम इसे सबसे लंबे समय तक काम करने वाले मुख्य शर्डिंग ऐक्सिस कहते हैं.

ज़्यादा जानकारी वाला डिज़ाइन

विवाद सुलझाने की हैरारकी

हम विवाद को हल करने की कई रणनीतियों को एक क्रम में बनाते हैं:

उपयोगकर्ता की तय की गई प्राथमिकताएं. शर्डिंग का तरीका लेख में, हमने बताया है कि प्रोग्राम को धीरे-धीरे अलग-अलग हिस्सों में बांटने के लिए, डाइमेंशन शर्डिंग में प्राथमिकताएं कैसे जोड़ी जा सकती हैं. उदाहरण के लिए, बैच पैरलललिज़्म -> मेगाट्रॉन -> ZeRO शर्डिंग. ऐसा करने के लिए, हम हर बार एक ही डाइमेंशन के लिए एक ही टारगेट लागू करते हैं. उदाहरण के लिए, i बार में हम उन सभी डाइमेंशन के लिए टारगेट लागू करते हैं जिनकी प्राथमिकता <=i है. साथ ही, बाकी सभी डाइमेंशन को अनदेखा कर देते हैं. हम यह भी पक्का करते हैं कि प्रॉपेगेशन, उपयोगकर्ता की तय की गई कम प्राथमिकता (>i) वाली शार्डिंग को बदल न दे. भले ही, पिछले दोहरावों के दौरान उन्हें अनदेखा किया गया हो.
ऑपरेशन के आधार पर प्राथमिकताएं. हम ऑपरेशन टाइप के आधार पर, शीयरिंग को प्रॉग्रेस करते हैं. "पास-थ्रू" ऑपरेशन (उदाहरण के लिए, एलिमेंट के हिसाब से ऑपरेशन और रीशेप) की प्राथमिकता सबसे ज़्यादा होती है. वहीं, शेप में बदलाव करने वाले ऑपरेशन (उदाहरण के लिए, बिंदु और कम करना) की प्राथमिकता कम होती है.
ज़्यादा प्रमोशन करना. बेहतर रणनीति के साथ, शार्डिंग को प्रसारित करें. बुनियादी रणनीति, सिर्फ़ बिना किसी विरोध के शार्डिंग को प्रचारित करती है, जबकि आक्रामक रणनीति विरोधों को हल करती है. ज़्यादा अग्रिमता से, संभावित कम्यूनिकेशन की कीमत पर, मेमोरी फ़ुटप्रिंट कम हो सकता है.
बुनियादी प्रॉपेगेशन. यह हैरारकी में प्रॉपेगेशन की सबसे कम रणनीति है. यह किसी भी तरह के विरोध को हल नहीं करती. इसके बजाय, यह ऐसे ऐक्सिस को प्रॉपेगेट करती है जो सभी ऑपरेंड और नतीजों के साथ काम करते हैं.

प्रॉपेगेशन की हैरारकी, जिसमें नीचे से ऊपर की ओर चार स्टैक दिखाए गए हैं. इन पर ये लेबल हैं: बुनियादी प्रॉपेगेशन, ऐग्रेशन प्रॉपेगेशन, ऑपरेशन की प्राथमिकता वाला प्रॉपेगेशन, उपयोगकर्ता की प्राथमिकता वाला प्रॉपेगेशन.

इस हैरारकी को नेस्ट किए गए for लूप के तौर पर समझा जा सकता है. उदाहरण के लिए, हर उपयोगकर्ता की प्राथमिकता के लिए, ऑप्ट-प्राथमिकता का पूरा प्रॉपेगेशन लागू होता है.

ऑपरेशन के लिए, डेटा को अलग-अलग हिस्सों में बांटने का नियम

शीयरिंग नियम, हर ऑपरेशन के लिए एक एब्स्ट्रैक्शन (अलग चीज़) पेश करता है. इससे, ऑपरेशन के टाइप और उनके एट्रिब्यूट के बारे में सोचे बिना, ऑपरेंड से नतीजों या ऑपरेंड के बीच शीयरिंग को प्रॉगेट करने के लिए, असल प्रॉगैगेशन एल्गोरिदम को ज़रूरी जानकारी मिलती है. इसमें, ऑपरेशन के हिसाब से लॉजिक को हटाकर, सिर्फ़ प्रॉपेगेशन के मकसद से सभी ऑपरेशन के लिए शेयर किया गया डेटा स्ट्रक्चर दिया जाता है. सबसे आसान रूप में, यह सिर्फ़ यह फ़ंक्शन उपलब्ध कराता है:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

इस नियम की मदद से, हम प्रॉपेगेशन एल्गोरिदम को एक बार में ही सामान्य तरीके से लिख सकते हैं. यह एल्गोरिदम, इस डेटा स्ट्रक्चर (OpShardingRule) पर आधारित होता है. इससे, कई ऑपरेशन में मिलते-जुलते कोड को दोहराने की ज़रूरत नहीं पड़ती. इससे, ऑपरेशन में गड़बड़ियों या गलत व्यवहार की संभावना बहुत कम हो जाती है.

आइए, matmul फ़ंक्शन के उदाहरण पर वापस जाएं.

एक ऐसा कोड जो प्रॉपेगेशन के दौरान ज़रूरी जानकारी को इकट्ठा करता है, जैसे कि डाइमेंशन के बीच के संबंधों को einsum नोटेशन के तौर पर लिखा जा सकता है:

(i, k), (k, j) -> (i, j)

इस एन्कोडिंग में, हर डाइमेंशन को एक फ़ैक्टर से मैप किया जाता है.

प्रोपगेशन इस मैपिंग का इस्तेमाल कैसे करता है: अगर किसी ऑपरेंड/नतीजे के डाइमेंशन को किसी ऐक्सिस के साथ शेयर किया गया है, तो प्रॉपेगेशन इस मैपिंग में उस डाइमेंशन के फ़ैक्टर को लुकअप करेगा. साथ ही, उसी फ़ैक्टर के साथ अन्य ऑपरेंड/नतीजों को उनके डाइमेंशन के साथ शेयर करेगा. साथ ही, (डुप्लीकेट बनाने के बारे में पहले की चर्चा के आधार पर) उन अन्य ऑपरेंड/नतीजों को भी डुप्लीकेट किया जा सकता है जिनमें उस ऐक्सिस के साथ वह फ़ैक्टर नहीं है.

कंपाउंड फ़ैक्टर: रीशेप करने के लिए नियम को बढ़ाना

कई ऑपरेशन में, जैसे कि matmul, हमें हर डाइमेंशन को सिर्फ़ एक फ़ैक्टर पर मैप करना होता है. हालांकि, डेटा को फिर से शेप करने के लिए, यह जानकारी काफ़ी नहीं है.

यहां दिया गया रीशेप फ़ंक्शन, दो डाइमेंशन को एक में मर्ज करता है:

%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

यहां, इनपुट के डाइमेंशन 0 और 1, दोनों आउटपुट के डाइमेंशन 0 से जुड़े हैं. मान लें कि हम इनपुट में फ़ैक्टर डालकर शुरुआत करते हैं:

(i,j,k) : i=2, j=4, k=32

आप देख सकते हैं कि अगर हमें आउटपुट के लिए एक ही फ़ैक्टर का इस्तेमाल करना है, तो हमें कई फ़ैक्टर का रेफ़रंस देने के लिए एक डाइमेंशन की ज़रूरत होगी:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

अगर रीशेप का इस्तेमाल किसी डाइमेंशन को बांटने के लिए किया जाता है, तो भी यही तरीका अपनाया जा सकता है:

%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>

यहां,

((ij), k) -> (i,j,k) : i=2, j=4, k=32

यहां साइज़ 8 का डाइमेंशन, मुख्य रूप से फ़ैक्टर 2 और 4 से बना है. इसलिए, हम फ़ैक्टर को (i,j,k) फ़ैक्टर कह रहे हैं.

ये फ़ैक्टर उन मामलों में भी काम कर सकते हैं जहां कोई ऐसा पूरा डाइमेंशन नहीं है जो किसी एक फ़ैक्टर से मेल खाता हो:

%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

इस उदाहरण से यह भी पता चलता है कि हमें फ़ैक्टर साइज़ क्यों स्टोर करने हैं - क्योंकि हम उन डाइमेंशन से आसानी से फ़ैक्टर साइज़ का पता नहीं लगा सकते.

कोर प्रोपेगेशन एल्गोरिदम

फ़ैक्टर के हिसाब से, अलग-अलग हिस्सों में बांटना

Shardy में, टेंसर, डाइमेंशन, और फ़ैक्टर की हैरारकी होती है. ये अलग-अलग लेवल पर डेटा दिखाते हैं. फ़ैक्टर एक सब-डाइमेंशन होता है. यह एक आंतरिक हैरारकी है, जिसका इस्तेमाल डेटा को अलग-अलग हिस्सों में बांटने के लिए किया जाता है. हर डाइमेंशन, एक या उससे ज़्यादा फ़ैक्टर से जुड़ा हो सकता है. डाइमेंशन और फ़ैक्टर के बीच मैपिंग को OpShardingRule से तय किया जाता है.

Shardy प्रोपेगेशन एल्गोरिदम दिखाने वाला स्कीमा.

Shardy, डाइमेंशन के बजाय फ़ैक्टर के साथ शर्डिंग ऐक्सिस को प्रॉपेगेट करता है. ऐसा करने के लिए, नीचे दी गई इमेज में दिखाए गए तीन चरणों का पालन करें:

प्रोजेक्ट DimSharding से FactorSharding
FactorSharding के स्पेस में, शर्डिंग ऐक्स को प्रॉपेगेट करना
अपडेट किया गया DimSharding देखने के लिए, अपडेट किया गया FactorSharding प्रोजेक्ट करें

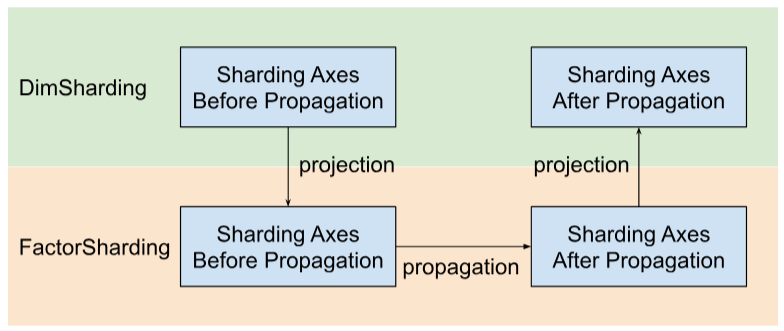
फ़ैक्टरशर्डिंग और डाइमशर्डिंग में, अलग-अलग हिस्सों में डेटा का बंटवारा दिखाने वाला स्कीमा.

फ़ैक्टर के हिसाब से, डेटा का बंटवारा करने की प्रोसेस को विज़ुअलाइज़ करना

हम नीचे दी गई टेबल का इस्तेमाल करके, शीयरिंग के प्रॉपेगेशन की समस्या और एल्गोरिदम को विज़ुअलाइज़ करेंगे.

	F0	F1	F2	साफ़ तौर पर डुप्लीकेट किए गए ऐक्सिस
T0
T1
T2

हर कॉलम किसी फ़ैक्टर को दिखाता है. F0 का मतलब है इंडेक्स 0 वाला फ़ैक्टर. हम फ़ैक्टर (कॉलम) के साथ-साथ, shardings को भी प्रॉग्रेस करते हैं.
हर पंक्ति, टेंसर को दिखाती है. T0, इंडेक्स 0 वाले टेंसर को दिखाता है. टेंसर, किसी खास ऑपरेशन में शामिल सभी ऑपरेंड और नतीजे होते हैं. किसी पंक्ति में मौजूद ऐक्सिस ओवरलैप नहीं हो सकते. किसी ऐक्सिस (या सब-ऐक्सिस) का इस्तेमाल, एक टेन्सर को कई बार सेगमेंट में बांटने के लिए नहीं किया जा सकता. अगर किसी ऐक्सिस को साफ़ तौर पर दोहराया गया है, तो हम उसका इस्तेमाल टेंसर को बांटने के लिए नहीं कर सकते.

इसलिए, हर सेल में फ़ैक्टर का एक हिस्सा होता है. आंशिक टेन्सर में कोई फ़ैक्टर मौजूद न हो. C = dot(A, B) के लिए टेबल नीचे दी गई है. जिन सेल में N होता है उनसे पता चलता है कि फ़ैक्टर टेंसर में नहीं है. उदाहरण के लिए, F2, T1 और T2 में है, लेकिन T0 में नहीं है.

`C = dot(A, B)`	F1 Non-contracting dim	F2 स्क्रीन की रोशनी को सामान्य लेवल से कम करने की सुविधा	F3 स्क्रीन की रोशनी को धीरे-धीरे कम करना
T0 = A		नहीं
T1 = B	नहीं
T2 = C			नहीं

sharding axes इकट्ठा करना और उन्हें प्रोपेगेट करना

हम प्रॉपेगेशन को विज़ुअलाइज़ करने के लिए, नीचे दिए गए एक आसान उदाहरण का इस्तेमाल करते हैं.

	F0	F1	F2
T0	"a"		"f"
T1	"a", "b"	"c", "d"	"g"
T2		"c", "e"

पहला चरण. हर फ़ैक्टर के साथ प्रॉपेगेट करने के लिए अक्ष ढूंढें. इन्हें (सबसे लंबे) काम करने वाले मुख्य sharding अक्ष भी कहा जाता है. इस उदाहरण के लिए, हम F0 के साथ ["a", "b"] और F1 के साथ ["c"] को प्रॉपगेट करते हैं. साथ ही, F2 के साथ कुछ भी प्रॉपगेट नहीं करते.

दूसरा चरण. नीचे दिया गया नतीजा पाने के लिए, फ़ैक्टर शर्डिंग को बड़ा करें.

	F0	F1	F2
T0	"a", "b"	"c"	"f"
T1	"a", "b"	"c", "d"	"g"
T2	"a", "b"	"c", "e"

डेटा फ़्लो ऑपरेशंस

ऊपर दिए गए प्रॉपेगेशन चरण की जानकारी, ज़्यादातर ऑपरेशन पर लागू होती है. हालांकि, कुछ मामलों में शीयर करने का नियम सही नहीं होता. ऐसे मामलों में, Shardy डेटा फ़्लो ऑपरेशन तय करता है.

किसी ऑपरेशन X का डेटा फ़्लो एज, सोर्स के एक सेट और टारगेट के एक सेट के बीच एक ब्रिज तय करता है, ताकि सभी सोर्स और टारगेट को एक ही तरह से शेयर किया जा सके. ऐसे ऑपरेशन के उदाहरणों में stablehlo::OptimizationBarrierOp, stablehlo::WhileOp, stablehlo::CaseOp, और sdy::ManualComputationOp शामिल हैं. आखिर में, ShardableDataFlowOpInterface को लागू करने वाले किसी भी ऑपरेशन को डेटा फ़्लो ऑपरेशन माना जाता है.

किसी ऑपरेशन में कई डेटा फ़्लो एज हो सकते हैं, जो एक-दूसरे के लिए ऑर्थोगोनल होते हैं. उदाहरण के लिए:

    y_0, ..., y_n = while (x_0, ..., x_n)
                    ((pred_arg_0,... , pred_arg_n) { ... })
                    ((body_arg_0,..., body_arg_n) {
                    ...
                    return return_value_0, ..., return_value_n
                    })

इस while op में n डेटा फ़्लो एज हैं: i-th डेटा फ़्लो एज, सोर्स x_i, return_value_i और टारगेट y_i, pred_arg_i, body_arg_i के बीच है.

Shardy, डेटा फ़्लो एज के सभी सोर्स और टारगेट के बीच, शीयरिंग को इस तरह प्रोपैगेट करेगा जैसे कि यह एक सामान्य ऑपरेशन हो. इसमें सोर्स, ऑपरेंड के तौर पर और टारगेट, नतीजों के तौर पर काम करेंगे. साथ ही, एक आइडेंटिटी sdy.op_sharding_rule भी होगी. इसका मतलब है कि फ़ॉरवर्ड प्रोपेगेशन, सोर्स से टारगेट तक होता है और बैकवर्ड प्रोपेगेशन, टारगेट से सोर्स तक होता है.

उपयोगकर्ता को कई तरीके लागू करने होंगे. इनमें, मालिक के ज़रिए हर डेटा फ़्लो एज के सोर्स और टारगेट पाने का तरीका बताना होगा. साथ ही, एज मालिक की शार्डिंग पाने और सेट करने का तरीका भी बताना होगा. मालिक, डेटा फ़्लो एज का वह टारगेट होता है जिसे उपयोगकर्ता तय करता है. इसका इस्तेमाल Shardy के प्रॉपेगेशन की प्रोसेस में किया जाता है. उपयोगकर्ता इसे अपनी पसंद के मुताबिक चुन सकता है, लेकिन यह स्टैटिक होना चाहिए.

उदाहरण के लिए, नीचे दिया गया custom_op:

  y_1, ..., y_n = custom_op (x_1, ..., x_n)
                  ((body_arg_1,..., body_arg_n) {
                    ...
                    return return_value_1, ..., return_value_n
                  })

इस कस्टम_ऑपरेशन में, डेटा फ़्लो एज के दो टाइप हैं: return_value_i (सोर्स) और y_i (टारगेट) के बीच n एज और x_i (सोर्स) और body_arg_i (टारगेट) के बीच n एज. इस मामले में, एज के मालिक और टारगेट एक ही होते हैं.

प्रजनन संग्रह की मदद से व्यवस्थित रहें अपनी प्राथमिकताओं के आधार पर, कॉन्टेंट को सेव करें और कैटगरी में बांटें.