Weitergabe von Einstellungsänderungen

Übersicht

Bei der Sharding-Ausbreitung werden die vom Nutzer angegebenen Shardings verwendet, um die nicht angegebenen Shardings von Tensoren (oder einer bestimmten Dimension von Tensoren) abzuleiten. Er durchläuft den Datenfluss (Verwendungs-/Definitionenketten) des Berechnungsgraphen in beiden Richtungen, bis ein fester Punkt erreicht wird, d.h., das Sharding kann nicht mehr geändert werden, ohne vorherige Sharding-Entscheidungen rückgängig zu machen.

Die Weiterleitung kann in Schritte unterteilt werden. Bei jedem Schritt wird eine bestimmte Operation betrachtet und basierend auf den Eigenschaften dieser Operation zwischen Tensoren (Operanden und Ergebnissen) weitergegeben. Nehmen wir als Beispiel eine Matrixmultiplikation: Wir würden zwischen der nicht schrumpfenden Dimension von lh oder rh zur entsprechenden Dimension des Ergebnisses oder zwischen der schrumpfenden Dimension von lh und rh fortschreiben.

Die Eigenschaften eines Vorgangs bestimmen die Verbindung zwischen entsprechenden Dimensionen in den Eingaben und Ausgaben und können als Sharding-Regel pro Vorgang abstrahiert werden.

Ohne Konfliktlösung würde bei einem Propagation-Schritt einfach so viel wie möglich weitergegeben, wobei die Konfliktachsen ignoriert würden. Wir bezeichnen dies als (längste) kompatible Haupt-Sharding-Achsen.

Detaillierte Konfiguration

Hierarchie der Konfliktlösung

Wir ordnen mehrere Strategien zur Konfliktlösung in einer Hierarchie an:

1. Benutzerdefinierte Prioritäten Im Artikel Sharding-Darstellung haben wir beschrieben, wie Dimensionen-Shardings Prioritäten zugeordnet werden können, um eine inkrementelle Partitionierung des Programms zu ermöglichen, z.B. Batch-Parallelität -> Megatron -> ZeRO-Sharding. Dazu wird die Weiterleitung in Iterationen angewendet. Bei Iteration i werden alle Dimensions-Shardings mit der Priorität <=i weitergegeben und alle anderen ignoriert. Außerdem wird dafür gesorgt, dass benutzerdefinierte Shardings mit niedrigerer Priorität (>i) bei der Propagation nicht überschrieben werden, auch wenn sie bei früheren Iterationen ignoriert wurden.
2. Betriebsbasierte Prioritäten Wir propagieren Shardings basierend auf dem Vorgangstyp. Die „Durchlauf“-Vorgänge (z.B. elementweise Vorgänge und „Neu formatieren“) haben die höchste Priorität, während Vorgänge mit Formtransformation (z.B. „Punkt“ und „Reduzieren“) eine niedrigere Priorität haben.
3. Aggressive Übernahme Shardings mit einer aggressiven Strategie weitergeben Bei der grundlegenden Strategie werden nur Shardings ohne Konflikte weitergegeben, während bei der aggressiven Strategie Konflikte behoben werden. Eine höhere Aggressivität kann den Arbeitsspeicherbedarf reduzieren, was jedoch zu einer schlechteren Kommunikation führen kann.
4. Grundlegende Replikation Dies ist die niedrigste Strategie der Weiterleitung in der Hierarchie, bei der keine Konfliktlösung erfolgt, sondern stattdessen Achsen weitergegeben werden, die mit allen Operanden und Ergebnissen kompatibel sind.

Diese Hierarchie kann als verschachtelte For-Schleifen interpretiert werden. Beispielsweise wird für jede Nutzerpriorität eine vollständige Übertragung der Betriebspriorität angewendet.

Regel für das Sharding von Vorgängen

Die Sharding-Regel führt eine Abstraktion aller Vorgänge ein, die dem tatsächlichen Propagationsalgorithmus die Informationen zur Verfügung stellt, die er zum Weitergeben von Shardings von Operanden zu Ergebnissen oder über Operanden hinweg benötigt, ohne sich Gedanken über bestimmte Vorgangstypen und ihre Attribute machen zu müssen. Dabei wird im Wesentlichen die betriebsspezifische Logik herausfaktorisiert und eine gemeinsame Darstellung (Datenstruktur) für alle Vorgänge nur zum Zweck der Weiterleitung bereitgestellt. In seiner einfachsten Form bietet es nur diese Funktion:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

Mit der Regel können wir den Propagation-Algorithmus nur einmal auf generische Weise schreiben, der auf dieser Datenstruktur (OpShardingRule) basiert, anstatt ähnliche Codeteile für viele Vorgänge zu replizieren. Dadurch wird das Risiko von Fehlern oder inkonsistentem Verhalten bei Vorgängen erheblich reduziert.

Kehren wir zum Beispiel mit matmul zurück.

Eine Codierung, die die Informationen enthält, die während der Übertragung benötigt werden, d.h. die Beziehungen zwischen Dimensionen, kann in Form der Einsum-Notation geschrieben werden:

(i, k), (k, j) -> (i, j)

Bei dieser Codierung wird jeder Dimension ein einzelner Faktor zugeordnet.

Verwendung dieser Zuordnung bei der Übertragung:Wenn eine Dimension eines Operanden/Ergebnisses entlang einer Achse gesplittet wird, wird bei der Übertragung der Faktor dieser Dimension in dieser Zuordnung ermittelt und andere Operanden/Ergebnisse werden entlang ihrer jeweiligen Dimension mit demselben Faktor gesplittet. Unter Umständen werden auch andere Operanden/Ergebnisse, die diesen Faktor entlang dieser Achse nicht haben, repliziert (siehe vorherige Erläuterungen zur Replikation).

Zusammengesetzte Faktoren: Regel für Umformungen erweitern

Bei vielen Vorgängen, z.B. matmul, müssen wir jede Dimension nur einem einzelnen Faktor zuordnen. Für eine Neugestaltung reicht sie jedoch nicht aus.

Mit der folgenden Umwandlung werden zwei Dimensionen zu einer zusammengeführt:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

Hier entsprechen sowohl Dimension 0 als auch Dimension 1 der Eingabe der Dimension 0 der Ausgabe. Angenommen, wir geben der Eingabe zuerst Faktoren:

(i,j,k) : i=2, j=4, k=32

Wenn wir dieselben Faktoren für die Ausgabe verwenden möchten, benötigen wir eine einzelne Dimension, um auf mehrere Faktoren zu verweisen:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

Das Gleiche gilt, wenn durch die Umwandlung eine Dimension aufgeteilt wird:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

Die Dimension der Größe 8 besteht hier im Wesentlichen aus den Faktoren 2 und 4. Deshalb nennen wir die Faktoren (i,j,k)-Faktoren.

Diese Faktoren können auch in Fällen verwendet werden, in denen es keine vollständige Dimension gibt, die einem der Faktoren entspricht:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Dieses Beispiel verdeutlicht auch, warum wir die Faktorgrößen speichern müssen, da sie sich nicht einfach aus den entsprechenden Dimensionen ableiten lassen.

Algorithmus zur Kernweitergabe

Sharding nach Faktoren weitergeben

In Shardy gibt es die Hierarchie von Tensoren, Dimensionen und Faktoren. Sie stellen Daten auf verschiedenen Ebenen dar. Ein Faktor ist eine untergeordnete Dimension. Es ist eine interne Hierarchie, die bei der Sharding-Replikation verwendet wird. Jede Dimension kann einem oder mehreren Faktoren entsprechen. Die Zuordnung zwischen Dimension und Faktor wird durch OpShardingRule definiert.

Shardy überträgt die Sharding-Achsen anhand von Faktoren anstelle von Dimensionen. Dazu sind drei Schritte erforderlich, wie in der Abbildung unten dargestellt.

1. DimSharding in FactorSharding umwandeln
2. Sharding-Achsen im Bereich von FactorSharding weitergeben
3. Aktualisiertes FactorSharding projizieren, um aktualisiertes DimSharding zu erhalten

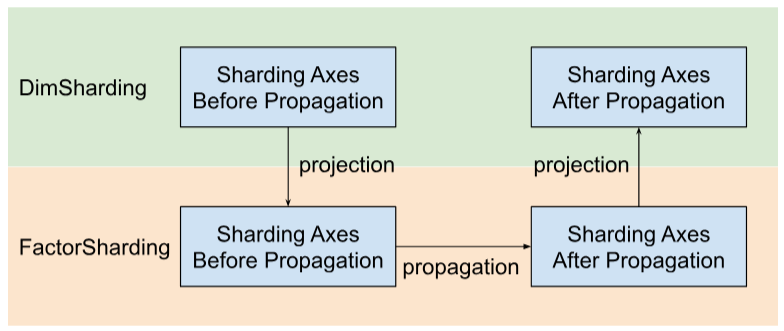
Visualisierung der Sharding-Ausbreitung entlang von Faktoren

In der folgenden Tabelle wird das Problem und der Algorithmus zur Sharding-Replikation veranschaulicht.

	F0	F1	F2	Explizit replizierte Achsen
T0
T1
T2

• Jede Spalte steht für einen Faktor. F0 steht für den Faktor mit dem Index 0. Wir leiten die Sharding-Informationen anhand von Faktoren (Spalten) weiter.
• Jede Zeile steht für einen Tensor. T0 bezieht sich auf den Tensor mit dem Index 0. Tensoren sind alle Operanden und Ergebnisse, die für einen bestimmten Vorgang erforderlich sind. Die Achsen in einer Zeile dürfen sich nicht überschneiden. Eine Achse (oder eine untergeordnete Achse) kann nicht mehrmals verwendet werden, um einen Tensor zu partitionieren. Wenn eine Achse explizit repliziert wird, können wir sie nicht zum Partitionieren des Tensors verwenden.

Jede Zelle steht also für ein Faktor-Sharding. Bei partiellen Tensoren kann ein Faktor fehlen. Die Tabelle für C = dot(A, B) finden Sie unten. Zellen mit einem N bedeuten, dass der Faktor nicht im Tensor enthalten ist. Beispiel: F2 ist in T1 und T2, aber nicht in T0.

C = dot(A, B)	F0 Batching dim	F1 – Nicht schrumpfendes Dimmen	F2 – Nicht schrumpfendes Dimmen	F3 – Kontrastminderung	Explizit replizierte Achsen
T0 = A			N
T1 = B		N
T2 = C				N

Sharding-Achsen erfassen und weitergeben

Im folgenden einfachen Beispiel wird die Weiterleitung veranschaulicht.

	F0	F1	F2	Explizit replizierte Achsen
T0	„a“		„f“
T1	„a“, „b“	„c“, „d“	„g“
T2		„c“, „e“

Schritt 1: Achsen finden, die entlang der einzelnen Faktoren fortgesetzt werden sollen (d. h. die (längsten) kompatiblen Haupt-Sharding-Achsen). In diesem Beispiel wird ["a", "b"] über F0, ["c"] über F1 und nichts über F2 weitergeleitet.

Schritt 2: Erweitern Sie die Faktor-Shardings, um das folgende Ergebnis zu erhalten.

	F0	F1	F2	Explizit replizierte Achsen
T0	„a“, „b“	"c"	„f“
T1	„a“, „b“	„c“, „d“	„g“
T2	„a“, „b“	„c“, „e“