การนำไปใช้งาน

ภาพรวม

การนำไปใช้งานการแยกข้อมูลจะใช้การแยกข้อมูลที่ผู้ใช้ระบุเพื่ออนุมานการแยกข้อมูลของ Tensor (หรือมิติข้อมูลเฉพาะของ Tensor) ที่ไม่ได้ระบุ โดยจะไปยังส่วนต่างๆ ของข้อมูล (เชน use-def) ของกราฟการประมวลผลทั้ง 2 ทิศทางจนกว่าจะถึงจุดคงที่ กล่าวคือ การแยกข้อมูลจะเปลี่ยนแปลงไม่ได้อีกต่อไปโดยไม่ต้องเลิกทำการตัดสินใจแยกข้อมูลก่อนหน้านี้

การนำไปใช้งานสามารถแบ่งออกเป็นขั้นตอนต่างๆ แต่ละขั้นตอนเกี่ยวข้องกับการพิจารณาการดำเนินการที่เฉพาะเจาะจงและการนำไปใช้กับเทนเซอร์ (Operand และผลลัพธ์) โดยอิงตามลักษณะของการดำเนินการนั้น ยกตัวอย่างเช่น matmul เราจะนำไปใช้กับมิติข้อมูลที่ไม่มีการหดตัวของ lhs หรือ rhs ไปยังมิติข้อมูลที่เกี่ยวข้องของผลลัพธ์ หรือระหว่างมิติข้อมูลที่หดตัวของ lhs และ rhs

ลักษณะของการดำเนินการจะกําหนดการเชื่อมต่อระหว่างมิติข้อมูลที่สอดคล้องกันในอินพุตและเอาต์พุต และสามารถแยกเป็นกฎการแยกข้อมูลตามการดำเนินการ

หากไม่มีการแก้ไขข้อขัดแย้ง ขั้นตอนการนำไปใช้จะนำไปใช้มากที่สุดเท่าที่จะทำได้โดยไม่สนใจแกนขัดแย้ง ซึ่งเราเรียกว่าแกนการแยกส่วนหลักที่เข้ากันได้ (ยาวที่สุด)

การออกแบบในรายละเอียด

ลําดับชั้นการแก้ไขข้อขัดแย้ง

เราใช้กลยุทธ์การแก้ไขข้อขัดแย้งหลายอย่างในลําดับชั้น ดังนี้

1. ลําดับความสําคัญที่กําหนดโดยผู้ใช้ ในการนำเสนอการแยกกลุ่ม เราได้อธิบายวิธีแนบลําดับความสําคัญกับการแยกกลุ่มมิติข้อมูลเพื่อให้สามารถแบ่งพาร์ติชันโปรแกรมได้มากขึ้น เช่น การทำขบวนการขนานแบบเป็นกลุ่ม -> Megatron -> การแยกกลุ่ม ZeRO ซึ่งทำได้โดยใช้การนำไปใช้งานในการวนซ้ำ โดยในการวนซ้ำ i เราจะนำไปใช้งานการแยกกลุ่มมิติข้อมูลทั้งหมดที่มีลําดับความสําคัญ <=i และละเว้นการนำไปใช้งานอื่นๆ ทั้งหมด นอกจากนี้ เรายังตรวจสอบว่าระบบจะไม่ลบล้างการแยกกลุ่มที่ผู้ใช้กำหนดซึ่งมีลําดับความสําคัญต่ำกว่า (>i) แม้ว่าระบบจะละเว้นการแยกกลุ่มดังกล่าวในระหว่างการวนซ้ำก่อนหน้านี้ก็ตาม
2. ลําดับความสําคัญตามการดําเนินการ เราจะเผยแพร่การแยกข้อมูลตามประเภทการดำเนินการ การดำเนินการ "ส่งผ่าน" (เช่น การดำเนินการกับองค์ประกอบและการเปลี่ยนรูปแบบ) จะมีลำดับความสำคัญสูงสุด ส่วนการดำเนินการที่มีการเปลี่ยนรูปแบบ (เช่น การคูณจุดและการดำเนินการลด) จะมีลำดับความสำคัญต่ำกว่า
3. การแพร่กระจายที่รุนแรง เผยแพร่การแยกข้อมูลด้วยกลยุทธ์เชิงรุก กลยุทธ์พื้นฐานจะเผยแพร่การแยกข้อมูลโดยไม่มีข้อขัดแย้งเท่านั้น ส่วนกลยุทธ์เชิงรุกจะแก้ไขข้อขัดแย้ง การตั้งค่าให้ก้าวร้าวมากขึ้นจะช่วยลดร่องรอยหน่วยความจําได้ แต่อาจทําให้การสื่อสารที่เป็นไปได้ลดลง
4. การนำไปใช้งานขั้นพื้นฐาน ซึ่งเป็นกลยุทธ์การนำไปใช้งานในระดับต่ำสุดในลําดับชั้น ที่ไม่ทำการแก้ไขข้อขัดแย้งใดๆ แต่นำไปใช้งานกับแกนที่เข้ากันได้ระหว่างโอเปอเรนดและผลลัพธ์ทั้งหมดแทน

ลําดับชั้นนี้ตีความได้ว่าเป็นวงวน for ที่ฝังอยู่ เช่น สําหรับลําดับความสําคัญของผู้ใช้แต่ละรายการ ระบบจะใช้การนำไปใช้งานลําดับความสําคัญของผู้ใช้แบบเต็ม

กฎการแยกกลุ่มการดำเนินการ

กฎการแยกข้อมูลออกเป็นส่วนๆ จะนําเสนอการแยกความคิดของการดำเนินการทั้งหมดซึ่งให้ข้อมูลที่จำเป็นในการนำไปใช้กับอัลกอริทึมการนำไปใช้งานจริงเพื่อนำไปใช้กับข้อมูลการแยกข้อมูลออกเป็นส่วนๆ จากตัวดำเนินการไปยังผลลัพธ์หรือในบรรดาตัวดำเนินการต่างๆ โดยไม่ต้องพิจารณาถึงประเภทการดำเนินการที่เฉพาะเจาะจงและคุณสมบัติของการดำเนินการเหล่านั้น โดยพื้นฐานแล้ว การดำเนินการนี้เป็นการแยกตรรกะเฉพาะของการดำเนินการและแสดงการนําเสนอที่แชร์ (โครงสร้างข้อมูล) สําหรับการดำเนินการทั้งหมดเพื่อวัตถุประสงค์ในการนำไปใช้เท่านั้น รูปแบบที่ง่ายที่สุดคือมีเพียงฟังก์ชันนี้

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

กฎนี้ช่วยให้เราเขียนอัลกอริทึมการนำไปใช้งานได้เพียงครั้งเดียวในลักษณะทั่วไปซึ่งอิงตามโครงสร้างข้อมูลนี้ (OpShardingRule) แทนการทําซ้ำโค้ดที่คล้ายกันในการดำเนินการหลายรายการ ซึ่งจะช่วยลดโอกาสที่จะเกิดข้อบกพร่องหรือลักษณะการทำงานที่ไม่สอดคล้องกันระหว่างการดำเนินการต่างๆ ได้อย่างมหาศาล

กลับไปดูตัวอย่าง matmul

การเข้ารหัสที่รวมข้อมูลที่จําเป็นในระหว่างการนำไปใช้งาน เช่น ความสัมพันธ์ระหว่างมิติข้อมูล สามารถเขียนในรูปแบบนิพจน์ einsum ดังนี้

(i, k), (k, j) -> (i, j)

ในการเข้ารหัสนี้ ระบบจะแมปมิติข้อมูลทุกรายการกับปัจจัยเดียว

วิธีที่การนำไปใช้งานใช้การแมปนี้: หากมิติข้อมูลของโอเปอเรนด/ผลลัพธ์มีการแบ่งกลุ่มตามแกน การนำไปใช้งานจะค้นหาปัจจัยของมิติข้อมูลนั้นในการแมปนี้ และแบ่งกลุ่มโอเปอเรนด/ผลลัพธ์อื่นๆ ตามมิติข้อมูลที่เกี่ยวข้องด้วยปัจจัยเดียวกัน และ (ขึ้นอยู่กับการพูดคุยก่อนหน้านี้เกี่ยวกับการทำซ้ำ) อาจทำซ้ำโอเปอเรนด/ผลลัพธ์อื่นๆ ที่ไม่มีปัจจัยนั้นตามแกนนั้นด้วย

ปัจจัยแบบผสม: การขยายกฎสำหรับการเปลี่ยนรูปแบบ

ในการดำเนินการหลายรายการ เช่น matmul เราจําเป็นต้องจับคู่มิติข้อมูลแต่ละรายการกับปัจจัยเดียวเท่านั้น แต่จะไม่เพียงพอสำหรับการเปลี่ยนรูปร่าง

การรีเชปต่อไปนี้จะผสานมิติข้อมูล 2 รายการเข้าด้วยกัน

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

ในกรณีนี้ มิติข้อมูล 0 และ 1 ของอินพุตจะสอดคล้องกับมิติข้อมูล 0 ของเอาต์พุต สมมติว่าเราเริ่มด้วยการกำหนดปัจจัยให้กับอินพุต

(i,j,k) : i=2, j=4, k=32

คุณจะเห็นว่าหากต้องการใช้ปัจจัยเดียวกันสําหรับเอาต์พุต เราต้องใช้มิติข้อมูลเดียวเพื่ออ้างอิงปัจจัยหลายรายการ

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

คุณทําแบบเดียวกันได้หากการรีเชปจะแยกมิติข้อมูล

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

มิติข้อมูลขนาด 8 นี้ประกอบด้วยปัจจัย 2 และ 4 เป็นหลัก เราจึงเรียกปัจจัยเหล่านี้ว่าปัจจัย (i,j,k)

ปัจจัยเหล่านี้ยังใช้ได้กับกรณีที่ไม่มีมิติข้อมูลแบบเต็มซึ่งสอดคล้องกับปัจจัยใดปัจจัยหนึ่งด้วย

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

ตัวอย่างนี้ยังเน้นย้ำถึงเหตุผลที่เราต้องจัดเก็บขนาดปัจจัยด้วย เนื่องจากเราไม่สามารถอนุมานขนาดปัจจัยจากมิติข้อมูลที่เกี่ยวข้องได้โดยง่าย

อัลกอริทึมการนำไปใช้งานหลัก

เผยแพร่การแยกกลุ่มตามปัจจัย

ใน Shardy เรามีลําดับชั้นของ Tensor, มิติข้อมูล และปัจจัย ซึ่งแสดงข้อมูลในระดับต่างๆ ปัจจัยคือมิติข้อมูลย่อย ซึ่งเป็นลําดับชั้นภายในที่ใช้ในการนำไปใช้กับ Sharding มิติข้อมูลแต่ละรายการอาจสอดคล้องกับปัจจัยอย่างน้อย 1 รายการ การแมประหว่างมิติข้อมูลกับปัจจัยจะกำหนดโดย OpShardingRule

Shardy จะเผยแพร่แกนการแยกตามปัจจัยแทนมิติข้อมูล โดยทําได้ 3 ขั้นตอนดังที่แสดงในรูปภาพด้านล่าง

1. เปลี่ยนการแยกมิติข้อมูลของโปรเจ็กต์เป็นการแยกปัจจัย
2. เผยแพร่แกนการแยกส่วนในพื้นที่ทำงานของ FactorSharding
3. คาดการณ์ FactorSharding ที่อัปเดตเพื่อรับ DimSharding ที่อัปเดต

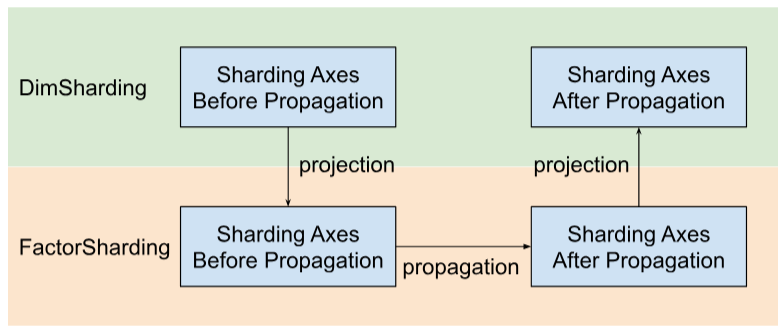
ภาพการแสดงการแพร่กระจายการแยกกลุ่มตามปัจจัย

เราจะใช้ตารางต่อไปนี้เพื่อแสดงภาพปัญหาและอัลกอริทึมของการปรับขนาดการแยกส่วน

	F0	F1	F2	แกนที่มีการจําลองอย่างชัดแจ้ง
T0
T1
T2

• แต่ละคอลัมน์แสดงปัจจัย F0 หมายถึงปัจจัยที่มีดัชนี 0 เราจะเผยแพร่การแยกส่วนตามปัจจัย (คอลัมน์)
• แต่ละแถวแสดงถึงเทนเซอร์ T0 หมายถึง Tensor ที่มีดัชนี 0 เทนเซอร์คือการดําเนินการและผลลัพธ์ทั้งหมดที่เกี่ยวข้องกับการดำเนินการหนึ่งๆ แกนในแถวต้องไม่ทับซ้อนกัน คุณใช้แกน (หรือแกนย่อย) เพื่อแบ่งเทนเซอร์ 1 รายการหลายครั้งไม่ได้ หากมีการจําลองแกนอย่างชัดแจ้ง เราจะใช้แกนนั้นเพื่อแบ่งพาร์ติชันเทนเซอร์ไม่ได้

ดังนั้นแต่ละเซลล์จึงแสดงการแยกกลุ่มปัจจัย ปัจจัยอาจขาดหายไปในเทนเซอร์บางส่วน ตารางสำหรับ C = dot(A, B) มีดังนี้ เซลล์ที่มี N หมายความว่าปัจจัยนั้นไม่ได้อยู่ในเทนเซอร์ เช่น F2 อยู่ใน T1 และ T2 แต่ไม่ได้อยู่ใน T0

C = dot(A, B)	F0 การปรับแสงเป็นสลัวแบบเป็นกลุ่ม	F1 หรี่แสงแบบไม่หด	F2 หรี่แสงแบบไม่หด	F3 หรี่แสงแบบหด	แกนที่มีการจําลองอย่างชัดแจ้ง
T0 = A			N
T1 = B		N
T2 = C				N

รวบรวมและเผยแพร่แกนการแยกข้อมูล

เราใช้ตัวอย่างง่ายๆ ที่แสดงด้านล่างเพื่อแสดงภาพการนำไปใช้งาน

	F0	F1	F2	แกนที่มีการจําลองอย่างชัดแจ้ง
T0	"a"		"f"
T1	"a", "b"	"c", "d"	"g"
T2		"c", "e"

ขั้นตอนที่ 1 ค้นหาแกนที่จะนำไปใช้กับแต่ละปัจจัย (หรือที่เรียกว่าแกนการแยกกลุ่มหลักที่เข้ากันได้ (ยาวที่สุด)) ในตัวอย่างนี้ เราจะส่ง ["a", "b"] ไปตาม F0 ส่ง ["c"] ไปตาม F1 และไม่ส่งข้อมูลใดๆ ไปตาม F2

ขั้นตอนที่ 2 ขยายการแยกส่วนปัจจัยเพื่อดูผลลัพธ์ต่อไปนี้

	F0	F1	F2	แกนที่มีการจําลองอย่างชัดแจ้ง
T0	"a", "b"	"c"	"f"
T1	"a", "b"	"c", "d"	"g"
T2	"a", "b"	"c", "e"