Propagazione

Panoramica

La propagazione dei sharding utilizza gli sharding specificati dall'utente per dedurre gli sharding non specificati dei tensori (o di una dimensione specifica dei tensori). Attraversa il flusso di dati (catene di definizioni di utilizzo) del grafo di calcolo in entrambe le direzioni fino a raggiungere un punto fisso, ovvero lo sharding non può più cambiare senza annullare le decisioni di sharding precedenti.

La propagazione può essere decomposta in passaggi. Ogni passaggio prevede l'esame di un'operazione specifica e la propagazione tra i tensori (operandi e risultati), in base alle caratteristiche dell'operazione. Prendendo come esempio una moltiplicazione matriciale, propagheremmo tra la dimensione non contrattante di lhs o rhs alla dimensione corrispondente del risultato o tra la dimensione contrattante di lhs e rhs.

Le caratteristiche di un'operazione determinano la connessione tra le dimensioni corrispondenti nei relativi input e output e possono essere riassunte come regola di sharding per operazione.

Senza la risoluzione dei conflitti, un passaggio di propagazione si propagherebbe semplicemente il più possibile ignorando gli assi in conflitto. Questi sono gli assi di suddivisione principali compatibili (più lunghi).

Progetto dettagliato

Gerarchia di risoluzione dei conflitti

Organizziamo più strategie di risoluzione dei conflitti in una gerarchia:

1. Priorità definite dall'utente. In Rappresentazione dello sharding, abbiamo descritto come le priorità possono essere associate agli sharding delle dimensioni per consentire il partitioning incrementale del programma, ad esempio eseguendo il parallelismo batch -> megatron -> lo sharding ZeRO. Questo viene ottenuto applicando la propagazione in iterazioni: nell'iterazione i propaghiamo tutti gli shard delle dimensioni con priorità <=i e ignoriamo tutti gli altri. Inoltre, ci assicuriamo che la propagazione non sostituisca gli sharding definiti dall'utente con priorità inferiore (>i), anche se vengono ignorati durante le iterazioni precedenti.
2. Priorità basate sulle operazioni. Propagare gli shard in base al tipo di operazione. Le operazioni "pass-through" (ad es. operazioni elementari e reshape) hanno la priorità più alta, mentre le operazioni con trasformazione della forma (ad es. dot e reduce) hanno una priorità inferiore.
3. Propagazione aggressiva. Propaga gli shard con una strategia aggressiva. La strategia di base propaga solo gli shard senza conflitti, mentre la strategia aggressiva risolve i conflitti. Un'aggressività maggiore può ridurre l'ingombro della memoria a scapito della potenziale comunicazione.
4. Propagazione di base. Si tratta della strategia di propagazione più bassa nella gerarchia, che non risolve i conflitti, ma propaga assi compatibili tra tutti gli operandi e i risultati.

Questa gerarchia può essere interpretata come cicli for nidificati. Ad esempio, per ogni priorità utente viene applicata una propagazione completa della priorità operativa.

Regola di suddivisione in parti dell'operazione

La regola di suddivisione introduce un'astrazione di ogni operazione che fornisce all'algoritmo di propagazione effettivo le informazioni di cui ha bisogno per propagare gli shard dagli operandi ai risultati o tra operandi e così via, senza dover ragionare su tipi di operazioni specifici e sui relativi attributi. Si tratta essenzialmente di eliminare la logica specifica dell'operazione e di fornire una rappresentazione condivisa (struttura di dati) per tutte le operazioni solo a scopo di propagazione. Nella sua forma più semplice, fornisce solo questa funzione:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

La regola ci consente di scrivere l'algoritmo di propagazione una sola volta in modo generico in base a questa struttura di dati (OpShardingRule), anziché replicare parti di codice simili in molte operazioni, riducendo notevolmente la possibilità di bug o comportamenti incoerenti tra le operazioni.

Torniamo all'esempio di matmul.

Una codifica che incapsula le informazioni necessarie durante la propagazione, ovvero le relazioni tra le dimensioni, può essere scritta sotto forma di notazione einsum:

(i, k), (k, j) -> (i, j)

In questa codifica, ogni dimensione è mappata a un singolo fattore.

In che modo la propagazione utilizza questa mappatura: se una dimensione di un operando/risultato è suddivisa in parti lungo un asse, la propagazione cercherà il fattore di quella dimensione in questa mappatura e suddividerà gli altri operandi/risultati lungo la rispettiva dimensione con lo stesso fattore e (in base alla discussione precedente sulla replica) potenzialmente anche altri operandi/risultati che non hanno questo fattore lungo quell'asse.

Fattori composti: estensione della regola per le ristrutturazioni

In molte operazioni, ad esempio matmul, è sufficiente mappare ogni dimensione a un singolo fattore. Tuttavia, non è sufficiente per le ristrutturazioni.

La seguente trasformazione unisce due dimensioni in una:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

In questo caso, entrambe le dimensioni 0 e 1 dell'input corrispondono alla dimensione 0 dell'output. Supponiamo di iniziare assegnando fattori all'input:

(i,j,k) : i=2, j=4, k=32

Puoi vedere che, se vogliamo utilizzare gli stessi fattori per l'output, abbiamo bisogno di una singola dimensione per fare riferimento a più fattori:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

Lo stesso può essere fatto se la trasformazione dovesse suddividere una dimensione:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

La dimensione di dimensione 8 qui è essenzialmente composta dai fattori 2 e 4, per questo chiamiamo fattori (i,j,k) i fattori.

Questi fattori possono essere utilizzati anche nei casi in cui non esiste una dimensione completa corrispondente a uno dei fattori:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Questo esempio sottolinea anche perché dobbiamo memorizzare le dimensioni dei fattori, poiché non possiamo dedurle facilmente dalle dimensioni corrispondenti.

Algoritmo di propagazione principale

Propagare le suddivisioni in base ai fattori

In Shardy abbiamo la gerarchia di tensori, dimensioni e fattori. Rappresentano i dati a diversi livelli. Un fattore è una dimensione secondaria. Si tratta di una gerarchia interna utilizzata nella propagazione del sharding. Ogni dimensione può corrispondere a uno o più fattori. La mappatura tra dimensione e fattore è definita da OpShardingRule.

Shardy propaga gli assi di suddivisione in base ai fattori anziché alle dimensioni. Per farlo, dobbiamo seguire tre passaggi, come mostrato nella figura seguente

1. Progetta DimSharding per FactorSharding
2. Propaga gli assi di suddivisione nello spazio di FactorSharding
3. Progetta il FactorSharding aggiornato per ottenere il DimSharding aggiornato

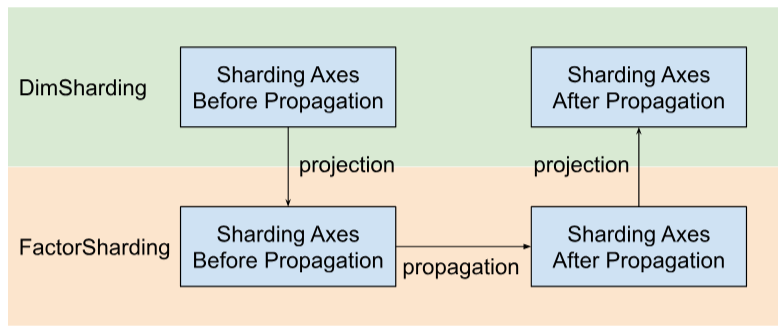
Visualizzazione della propagazione del partizionamento in base ai fattori

Utilizzeremo la seguente tabella per visualizzare il problema e l'algoritmo di propagazione del sharding.

	F0	F1	F2	Assi replicati esplicitamente
T0
T1
T2

• Ogni colonna rappresenta un fattore. F0 indica il fattore con indice 0. Propagare le suddivisioni in base ai fattori (colonne).
• Ogni riga rappresenta un tensore. T0 si riferisce al tensore con indice 0. I tensori sono tutti gli operandi e i risultati coinvolti per un'operazione specifica. Gli assi in una riga non possono sovrapporsi. Un asse (o un asse secondario) non può essere utilizzato per partizionare un tensor più volte. Se un asse viene replicato esplicitamente, non possiamo utilizzarlo per partizionare il tensore.

Pertanto, ogni cella rappresenta un'organizzazione in parti di un fattore. Nei tensori parziali può mancare un fattore. La tabella per C = dot(A, B) è riportata di seguito. Le celle contenenti un N suggeriscono che il fattore non è nel tensore. Ad esempio, F2 è in T1 e T2, ma non in T0.

C = dot(A, B)	F0 Batching dim	Dimensione F1 non contrattuale	F2 Dimming non contrattabile	F3 Dimming contrattabile	Assi replicati esplicitamente
T0 = A			No
T1 = B		No
T2 = C				No

Raccogliere e propagare gli assi di suddivisione

Utilizziamo un semplice esempio mostrato di seguito per visualizzare la propagazione.

	F0	F1	F2	Assi replicati esplicitamente
T0	"a"		"f"
T1	"a", "b"	"c", "d"	"g"
T2		"c", "e"

Passaggio 1. Trova gli assi da propagare lungo ogni fattore (ovvero gli assi di suddivisione principali (più lunghi) compatibili). Per questo esempio, propaghiamo ["a", "b"] lungo F0, propaghiamo ["c"] lungo F1 e non propaghiamo nulla lungo F2.

Passaggio 2. Espandi le suddivisioni dei fattori per ottenere il seguente risultato.

	F0	F1	F2	Assi replicati esplicitamente
T0	"a", "b"	"c"	"f"
T1	"a", "b"	"c", "d"	"g"
T2	"a", "b"	"c", "e"