적용

개요

샤딩 전파는 사용자가 지정한 샤딩을 사용하여 텐서 (또는 텐서의 특정 측정기준)의 지정되지 않은 샤딩을 추론합니다. 고정된 지점에 도달할 때까지 계산 그래프의 데이터 흐름 (use-def 체인)을 양방향으로 탐색합니다. 즉, 이전 샤딩 결정을 실행취소하지 않고는 더 이상 샤딩을 변경할 수 없습니다.

전파는 단계로 분해할 수 있습니다. 각 단계에는 특정 연산을 살펴보고 해당 연산의 특성에 따라 텐서 (피연산자 및 결과) 간에 전파하는 작업이 포함됩니다. matmul을 예로 들면 왼쪽 항이나 오른쪽 항의 비축소 차원을 결과의 해당 차원으로 전파하거나 왼쪽 항과 오른쪽 항의 축소 차원 간에 전파합니다.

연산의 특성은 입력과 출력의 상응하는 측정기준 간의 연결을 결정하며 연산별 샤딩 규칙으로 추상화할 수 있습니다.

충돌 해결이 없으면 전파 단계는 충돌하는 축을 무시하면서 최대한 많이 전파합니다. 이를 (가장 긴) 호환되는 주요 샤딩 축이라고 합니다.

세부 설계

충돌 해결 계층 구조

계층 구조에서 여러 충돌 해결 전략을 구성합니다.

1. 사용자 정의 우선순위. 샤딩 표현에서는 프로그램의 증분 파티셔닝(예: 일괄 병렬 처리 -> 메가트론 -> ZeRO 샤딩)을 허용하도록 차원 샤딩에 우선순위를 연결하는 방법을 설명했습니다. 이는 반복에서 전파를 적용하여 실행됩니다. 반복 i에서 우선순위가 <=i인 모든 측정기준 샤딩을 전파하고 다른 모든 측정기준 샤딩은 무시합니다. 또한 이전 반복 중에 무시되더라도 우선순위가 낮은 사용자 정의 샤딩 (>i)이 전파 중에 재정의되지 않도록 합니다.
2. 작업 기반 우선순위 작업 유형에 따라 샤딩을 전파합니다. '패스 스루' 연산 (예: 요소별 연산 및 모양 변경)의 우선순위가 가장 높고, 도형 변환이 포함된 연산 (예: dot 및 reduce)의 우선순위가 더 낮습니다.
3. 적극적인 전파. 공격적인 전략으로 샤딩을 전파합니다. 기본 전략은 충돌이 없는 샤딩만 전파하는 반면 공격적인 전략은 충돌을 해결합니다. 공격성이 높을수록 잠재적인 통신 비용으로 메모리 공간을 줄일 수 있습니다.
4. 기본 전파 이는 계층 구조에서 가장 낮은 전파 전략으로, 충돌 해결을 수행하지 않고 대신 모든 피연산자와 결과 간에 호환되는 축을 전파합니다.

이 계층 구조는 중첩된 for 루프로 해석할 수 있습니다. 예를 들어 각 사용자 우선순위에 전체 작업 우선순위 전파가 적용됩니다.

작업 샤딩 규칙

샤딩 규칙은 특정 연산 유형 및 속성에 관해 추론할 필요 없이 실제 전파 알고리즘에 피연산자에서 결과로 또는 피연산자 간에 샤딩을 전파하는 데 필요한 정보를 제공하는 모든 연산의 추상화를 도입합니다. 이는 기본적으로 연산별 로직을 분리하고 전파 전용으로 모든 연산에 공유 표현 (데이터 구조)을 제공하는 것입니다. 가장 간단한 형태에서는 다음 함수만 제공합니다.

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

이 규칙을 사용하면 여러 작업에 유사한 코드 조각을 복제하는 대신 이 데이터 구조 (OpShardingRule)를 기반으로 하는 일반적인 방식으로 전파 알고리즘을 한 번만 작성할 수 있으므로 작업 전반에서 버그 또는 일관되지 않은 동작이 발생할 가능성이 크게 줄어듭니다.

matmul 예로 돌아가 보겠습니다.

전파 중에 필요한 정보(즉, 측정기준 간의 관계)를 캡슐화하는 인코딩은 einsum 표기법 형식으로 작성할 수 있습니다.

(i, k), (k, j) -> (i, j)

이 인코딩에서는 모든 측정기준이 단일 요인에 매핑됩니다.

전파에서 이 매핑을 사용하는 방법: 피연산자/결과의 측정기준이 축을 따라 샤딩된 경우 전파는 이 매핑에서 해당 측정기준의 계수를 조회하고 동일한 계수로 각 측정기준을 따라 다른 피연산자/결과를 샤딩합니다. 또한 (앞서 설명한 복제에 따라) 해당 축을 따라 해당 계수가 없는 다른 피연산자/결과를 복제할 수도 있습니다.

복합 요인: 리셰이프 규칙 확장

matmul과 같은 많은 연산에서는 각 측정기준을 단일 계수에 매핑하기만 하면 됩니다. 하지만 리셰이프에는 충분하지 않습니다.

다음 리셰이프는 두 측정기준을 하나로 병합합니다.

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

여기서 입력의 차원 0과 1은 모두 출력의 차원 0에 해당합니다. 입력에 계수를 제공하는 것으로 시작해 보겠습니다.

(i,j,k) : i=2, j=4, k=32

출력에 동일한 요인을 사용하려면 여러 요인을 참조할 수 있는 단일 측정기준이 필요합니다.

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

리셰이프가 측정기준을 분할하는 경우에도 동일한 작업을 할 수 있습니다.

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

여기서 크기가 8인 크기는 본질적으로 2와 4로 구성되므로 (i,j,k) 요소라고 합니다.

이러한 요인은 다음과 같은 경우에 사용할 수도 있습니다.

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

이 예에서는 요소 크기를 저장해야 하는 이유도 강조합니다. 해당 크기를 상응하는 크기에서 쉽게 추론할 수 없기 때문입니다.

핵심 전파 알고리즘

요인별로 샤딩 전파

Shardy에는 텐서, 측정기준, 계수의 계층 구조가 있습니다. 이는 다양한 수준의 데이터를 나타냅니다. 요소는 하위 측정기준입니다. 샤딩 전파에 사용되는 내부 계층 구조입니다. 각 측정기준은 하나 이상의 요인에 해당할 수 있습니다. 측정기준과 계수 간의 매핑은 OpShardingRule에 의해 정의됩니다.

Shardy는 측정기준 대신 요인에 따라 샤딩 축을 전파합니다. 이를 위해 아래 그림과 같이 세 단계를 거칩니다.

1. DimSharding을 FactorSharding으로 프로젝트
2. FactorSharding의 공간에서 샤딩 축 전파
3. 업데이트된 DimSharding을 가져오기 위해 업데이트된 FactorSharding을 프로젝션합니다.

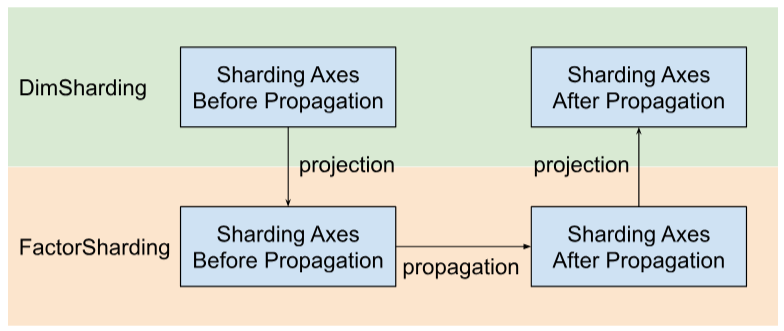
요인별 샤딩 전파 시각화

다음 표를 사용하여 샤딩 전파 문제와 알고리즘을 시각화합니다.

	F0	F1	F2	명시적으로 복제된 축
T0
T1
T2

• 각 열은 요인을 나타냅니다. F0은 인덱스가 0인 계수를 의미합니다. 계수 (열)를 따라 샤딩을 전파합니다.
• 각 행은 텐서를 나타냅니다. T0은 색인이 0인 텐서를 나타냅니다. 텐서는 특정 연산과 관련된 모든 피연산자 및 결과입니다. 행의 축은 겹칠 수 없습니다. 축 (또는 하위 축)을 사용하여 하나의 텐서를 여러 번 분할할 수는 없습니다. 축이 명시적으로 복제된 경우 이를 사용하여 텐서를 분할할 수 없습니다.

따라서 각 셀은 요인 샤딩을 나타냅니다. 부분 텐서에는 계수가 누락될 수 있습니다. C = dot(A, B)의 표는 아래와 같습니다. N가 포함된 셀은 인자가 텐서에 없다는 것을 의미합니다. 예를 들어 F2는 T1 및 T2에 있지만 T0에는 없습니다.

C = dot(A, B)	F0 일괄 처리 어둡게	F1 비계약 dim	F2 비축소 어둡게	F3 수축 어둡게	명시적으로 복제된 축
T0 = A			N
T1 = B		N
T2 = C				N

샤딩 축 수집 및 전파

아래에 표시된 간단한 예를 사용하여 전파를 시각화합니다.

	F0	F1	F2	명시적으로 복제된 축
T0	'a'		"f"
T1	"a", "b"	'c', 'd'	"g"
T2		"c", "e"

1단계: 각 요인(즉, 호환되는 가장 긴 주요 샤딩 축)을 따라 전파할 축을 찾습니다. 이 예에서는 F0을 따라 ["a", "b"]를 전파하고, F1을 따라 ["c"]를 전파하며, F2를 따라 아무것도 전파하지 않습니다.

2단계: 요소 샤딩을 펼쳐 다음과 같은 결과를 얻습니다.

	F0	F1	F2	명시적으로 복제된 축
T0	"a", "b"	"c"	"f"
T1	"a", "b"	'c', 'd'	"g"
T2	'a', 'b'	"c", "e"