Yayılma

Genel Bakış

Bölme yayma, kullanıcı tarafından belirtilen bölmelere (veya tenzorların belirli boyutlarına) göre belirtilmeyen bölmelerin tahmin edilmesi için kullanıcı tarafından belirtilen bölmelerden yararlanır. Sabit bir noktaya ulaşılana kadar hesaplama grafiğinin veri akışını (kullanım-tanım zincirleri) her iki yönde de tarar. Yani, önceki bölme kararları geri alınmadan bölme artık değiştirilemez.

Yayma işlemi adımlara ayrılabilir. Her adımda belirli bir işleme bakılır ve bu işlemin özelliklerine göre tensörler (operandlar ve sonuçlar) arasında yayılma işlemi gerçekleştirilir. Örnek olarak bir matmul işlevini ele alalım. Bu işlevde, sol veya sağ tarafın daralmayan boyutu ile sonucun ilgili boyutu arasında ya da sol ve sağ tarafın daralan boyutu arasında yayılma işlemi gerçekleştiririz.

Bir işlemin özellikleri, giriş ve çıkışlarındaki karşılık gelen boyutlar arasındaki bağlantıyı belirler ve işlem başına bölümleme kuralı olarak soyutlanabilir.

Çakışma çözümü olmadan bir dağıtım adımı, çakışan eksenleri yoksayarken mümkün olduğunca fazla dağıtım yapar. Buna (en uzun) uyumlu ana bölme eksenleri denir.

Ayrıntılı Tasarım

Çatışma çözümü hiyerarşisi

Hiyerarşide birden fazla çakışma çözümü stratejisi oluştururuz:

1. Kullanıcı tanımlı öncelikler. Bölünme Temsili bölümünde, programın artımlı bölümlenmesine (ör. toplu paralellik -> megatron -> ZeRO bölme) izin vermek için boyut bölmelerine önceliklerin nasıl eklenebileceğini açıklamıştık. Bu, iterasyonlarda dağıtım uygulanarak elde edilir. i iterasyonunda, <=i önceliğine sahip tüm boyut bölmelerini dağıtır ve diğer tümünü yoksayarız. Ayrıca, önceki iterasyonlarda yoksayılmış olsalar bile kullanıcı tanımlı daha düşük öncelikli (>i) parçalara dağıtımların dağıtımın geçersiz kılmayacağından emin oluruz.
2. İşleme dayalı öncelikler. Bölme işlemlerini işlem türüne göre dağıtırız. "Geçiş" işlemleri (ör. öğe bazında işlemler ve yeniden şekillendirme) en yüksek önceliğe sahipken şekil dönüşümü içeren işlemler (ör. nokta ve azaltma) daha düşük önceliğe sahiptir.
3. Agresif yayılma. Bölme işlemlerini agresif bir stratejiyle dağıtın. Temel strateji yalnızca çakışması olmayan parçaları dağıtırken agresif strateji çakışmaları çözer. Daha yüksek agresiflik, olası iletişim pahasına bellek kullanımını azaltabilir.
4. Temel Yayma Hiyerarşideki en düşük yayma stratejisidir. Çakışma çözümü yapmaz, bunun yerine tüm işlevler ve sonuçlar arasında uyumlu olan eksenleri yayar.

Bu hiyerarşi, iç içe yerleştirilmiş for döngüleri olarak yorumlanabilir. Örneğin, her kullanıcı önceliği için tam işlem önceliği yayımı uygulanır.

İşlem bölme kuralı

Bölme kuralında, belirli işlem türleri ve özellikleri hakkında düşünmek zorunda kalmadan bölme işlemlerini operatörlerden sonuçlara veya operatörler arasında vb. yaymak için gereken bilgileri gerçek yayma algoritmasına sağlayan her işlemin soyut bir versiyonu sunulur. Bu, temel olarak işleme özgü mantığı ortadan kaldırır ve yalnızca dağıtım amacıyla tüm işlemler için ortak bir temsil (veri yapısı) sağlar. En basit haliyle yalnızca şu işlevi sağlar:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

Bu kural, benzer kod parçalarını birçok işlemde kopyalamak yerine, dağıtım algoritmasını yalnızca bir kez bu veri yapısına (OpShardingRule) dayalı genel bir şekilde yazmamıza olanak tanır. Böylece, işlemlerde hata veya tutarsız davranış olasılığını büyük ölçüde azaltır.

matmul örneğine dönelim.

Yayma sırasında gerekli olan bilgileri (ör. boyutlar arasındaki ilişkiler) kapsayan bir kodlama, einsum gösterimi biçiminde yazılabilir:

(i, k), (k, j) -> (i, j)

Bu kodlamada her boyut tek bir faktörle eşlenir.

Yayınlama bu eşlemeyi nasıl kullanır? Bir operandın/sonucun boyutu bir eksen boyunca parçalara ayrılırsa yayınlama, bu eşlemede ilgili boyutun faktörünü arar ve diğer operandları/sonuçları kendi boyutları boyunca aynı faktörle parçalara ayırır. Ayrıca (kopyalama hakkındaki önceki tartışmaya tabi olarak) bu eksende bu faktöre sahip olmayan diğer operandları/sonuçları da kopyalayabilir.

Bileşik faktörler: yeniden şekillendirme kurallarının genişletilmesi

Birçok işlemde (ör. matmul) her boyutu tek bir faktörle eşlememiz yeterlidir. Ancak yeniden şekillendirme için yeterli değildir.

Aşağıdaki yeniden şekillendirme işleminde iki boyut tek bir boyutta birleştirilir:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

Burada, girişin hem 0 hem de 1 boyutu, çıktının 0 boyutuna karşılık gelir. Giriş için faktörler vererek başlayalım:

(i,j,k) : i=2, j=4, k=32

Çıkış için aynı faktörleri kullanmak istiyorsak birden fazla faktöre referans vermek üzere tek bir boyuta ihtiyacımız olduğunu görebilirsiniz:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

Yeniden şekillendirme işlemi bir boyutu bölseydi de aynı işlem yapılabilir:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

Buradaki 8 boyutu temel olarak 2 ve 4 faktörlerinden oluşur. Bu nedenle faktörleri (i, j, k) faktörleri olarak adlandırıyoruz.

Bu faktörler, faktörlerden birine karşılık gelen tam bir boyutun olmadığı durumlarda da kullanılabilir:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Bu örnekte, faktör boyutlarını neden saklamamız gerektiği de vurgulanmıştır. Çünkü bunları ilgili boyutlardan kolayca çıkaramayız.

Temel Yayma Algoritması

Bölme işlemlerini faktörlere göre dağıtma

Shardy'de tensörler, boyutlar ve faktörler hiyerarşisi vardır. Bunlar, verileri farklı düzeylerde temsil eder. Faktör, bir alt boyuttur. Bölme yayma işleminde kullanılan dahili bir hiyerarşidir. Her boyut bir veya daha fazla faktöre karşılık gelebilir. Boyut ile faktör arasındaki eşleme, OpShardingRule tarafından tanımlanır.

Shardy, bölme eksenlerini boyutlar yerine faktörler boyunca dağıtır. Bunun için aşağıdaki şekilde gösterilen üç adımdan yararlanırız.

1. Proje DimSharding'den FactorSharding'e
2. FactorSharding alanında bölme eksenlerini yayma
3. Güncellenmiş DimSharding'i almak için güncellenmiş FactorSharding'i projelendirin

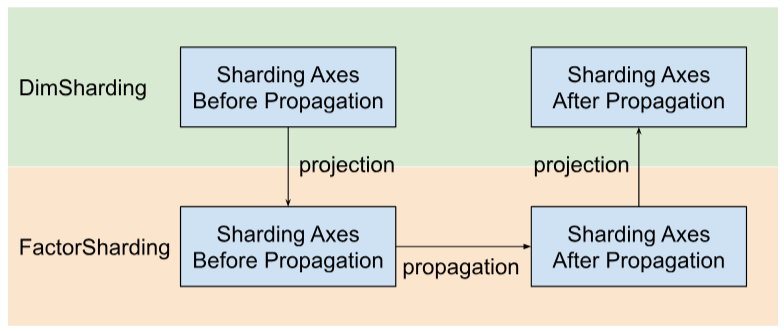
Faktörlere Göre Bölme Yayılımının Görselleştirilmesi

Bölme yayma sorununu ve algoritmasını görselleştirmek için aşağıdaki tabloyu kullanacağız.

	F0	F1	F2	Açıkça kopyalanan eksenler
T0
Ş1
Ş2

• Her sütun bir faktörü temsil eder. F0, dizini 0 olan faktör anlamına gelir. Bölme işlemlerini faktörlere (sütunlar) dağıtırız.
• Her satır bir tensörü temsil eder. T0, 0 dizine sahip tenzoru ifade eder. Tensörler, belirli bir işlemle ilgili tüm operatörler ve sonuçlardır. Bir satırdaki eksenler çakışamaz. Bir eksen (veya alt eksen), bir tensörü birden çok kez bölmek için kullanılamaz. Açıkça kopyalanan bir eksen, tensörü bölümlemek için kullanılamaz.

Bu nedenle, her hücre bir faktör bölme işlemini temsil eder. Kısmi tensörlerde bir faktör eksik olabilir. C = dot(A, B) için tablo aşağıda verilmiştir. N içeren hücreler, faktörün tensörde olmadığını gösterir. Örneğin, F2, T1 ve T2'de ancak T0'da değildir.

C = dot(A, B)	F0 Grup halinde karartma	F1 Daraltmayan karartma	F2 Daraltmayan karartma	F3 Daraltılmış loş	Açıkça kopyalanan eksenler
T0 = A			H
T1 = B		H
T2 = C				H

Bölme eksenlerini toplama ve dağıtma

Yayılımı görselleştirmek için aşağıda gösterilen basit bir örneği kullanırız.

	F0	F1	F2	Açıkça kopyalanan eksenler
T0	"a"		"f"
Ş1	"a", "b"	"c", "d"	"g"
Ş2		"c", "e"

1.adım: Her faktör boyunca dağıtılacak eksenleri (diğer adıyla (en uzun) uyumlu ana bölme eksenleri) bulun. Bu örnekte, ["a", "b"] değerini F0 boyunca, ["c"] değerini F1 boyunca ve F2 boyunca hiçbir değeri dağıtmayız.

2.adım: Aşağıdaki sonucu elde etmek için faktör bölmelerini genişletin.

	F0	F1	F2	Açıkça kopyalanan eksenler
T0	"a", "b"	"c"	"f"
Ş1	"a", "b"	"c", "d"	"g"
Ş2	"a", "b"	"c", "e"