Propagation

Présentation

La propagation de fractionnement utilise les fractionnements spécifiés par l'utilisateur pour inférer les fractionnements non spécifiés des tenseurs (ou la dimension spécifique des tenseurs). Il traverse le flux de données (chaînes d'utilisation-définition) du graphe de calcul dans les deux sens jusqu'à ce qu'un point fixe soit atteint, c'est-à-dire que le fractionnement ne peut plus changer sans annuler les décisions de fractionnement précédentes.

La propagation peut être décomposée en étapes. Chaque étape consiste à examiner une opération spécifique et à la propager entre les tenseurs (opérandes et résultats), en fonction des caractéristiques de cette opération. Prenons un matmul comme exemple. Nous propagerions entre la dimension non contractante de lhs ou rhs vers la dimension correspondante du résultat, ou entre la dimension contractante de lhs et rhs.

Les caractéristiques d'une opération déterminent la connexion entre les dimensions correspondantes dans ses entrées et ses sorties, et peuvent être abstraites en tant que règle de fractionnement par opération.

Sans résolution de conflit, une étape de propagation se propagerait simplement autant que possible en ignorant les axes en conflit. Nous appelons cela les axes de partitionnement principaux (les plus longs) compatibles.

Conception détaillée

Hiérarchie de résolution des conflits

Nous composons plusieurs stratégies de résolution de conflits dans une hiérarchie:

1. Priorités définies par l'utilisateur Dans la section Représentation du fractionnement, nous avons décrit comment des priorités peuvent être associées aux fractionnements de dimension pour permettre un partitionnement incrémentiel du programme, par exemple en effectuant un parallélisme par lot -> mégatron -> fractionnement ZERO. Pour ce faire, nous appliquons la propagation en itérations. À l'itération i, nous propageons tous les fractionnements de dimension ayant la priorité <=i et ignorons tous les autres. Nous nous assurons également que la propagation ne remplace pas les fractionnements définis par l'utilisateur avec une priorité inférieure (>i), même s'ils sont ignorés lors des itérations précédentes.
2. Priorités basées sur l'opération Nous propageons les fractionnements en fonction du type d'opération. Les opérations de "pass-through" (par exemple, les opérations par élément et la refonte) ont la priorité la plus élevée, tandis que les opérations avec transformation de forme (par exemple, le point et la réduction) ont une priorité plus faible.
3. Propagation agressive. Propagez les fractionnements avec une stratégie agressive. La stratégie de base ne propage que les fractionnements sans conflit, tandis que la stratégie agressive résout les conflits. Une agressivité plus élevée peut réduire l'empreinte mémoire au détriment de la communication potentielle.
4. Propagation de base Il s'agit de la stratégie de propagation la plus basse dans la hiérarchie. Elle ne résout aucun conflit, mais propage plutôt des axes compatibles entre tous les opérandes et les résultats.

Cette hiérarchie peut être interprétée comme des boucles for imbriquées. Par exemple, pour chaque priorité utilisateur, une propagation complète de la priorité d'opération est appliquée.

Règle de fractionnement des opérations

La règle de partitionnement introduit une abstraction de chaque opération qui fournit à l'algorithme de propagation réel les informations dont il a besoin pour propager les partitionnements des opérandes aux résultats ou entre les opérandes, etc., sans avoir à raisonner sur des types d'opérations spécifiques et leurs attributs. Il s'agit essentiellement de factoriser la logique spécifique à l'opération et de fournir une représentation partagée (structure de données) pour toutes les opérations à des fins de propagation uniquement. Dans sa forme la plus simple, il ne fournit que cette fonction:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

La règle nous permet d'écrire l'algorithme de propagation une seule fois de manière générique, basée sur cette structure de données (OpShardingRule), au lieu de répliquer des éléments de code similaires dans de nombreuses opérations, ce qui réduit considérablement le risque de bugs ou de comportements incohérents entre les opérations.

Revenons à l'exemple matmul.

Un encodage qui encapsule les informations nécessaires lors de la propagation, c'est-à-dire les relations entre les dimensions, peut être écrit sous la forme de la notation einsum:

(i, k), (k, j) -> (i, j)

Dans cet encodage, chaque dimension est mappée à un seul facteur.

Comment la propagation utilise-t-elle ce mappage ? Si une dimension d'une opérande/d'un résultat est partitionnée selon une axe, la propagation recherche le facteur de cette dimension dans ce mappage et partitionne les autres opérandes/résultats selon leur dimension respective avec le même facteur. (et, sous réserve de la discussion précédente sur la réplication, elle peut également répliquer d'autres opérandes/résultats qui ne disposent pas de ce facteur selon cet axe).

Facteurs combinés: extension de la règle pour les refontes

Dans de nombreuses opérations, par exemple matmul, il suffit de mapper chaque dimension à un seul facteur. Toutefois, cela ne suffit pas pour les redimensionnements.

La refonte suivante fusionne deux dimensions en une:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

Ici, les dimensions 0 et 1 de l'entrée correspondent à la dimension 0 de la sortie. Supposons que nous commencions par définir des facteurs pour l'entrée:

(i,j,k) : i=2, j=4, k=32

Vous pouvez constater que si nous souhaitons utiliser les mêmes facteurs pour la sortie, nous aurions besoin d'une seule dimension pour faire référence à plusieurs facteurs:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

Vous pouvez faire de même si la refonte doit diviser une dimension:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

La dimension de taille 8 ici est essentiellement composée des facteurs 2 et 4, c'est pourquoi nous appelons les facteurs (i,j,k) facteurs.

Ces facteurs peuvent également fonctionner dans les cas où aucune dimension complète ne correspond à l'un d'eux:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Cet exemple souligne également pourquoi nous devons stocker les tailles de facteur, car nous ne pouvons pas les déduire facilement des dimensions correspondantes.

Algorithme de propagation de base

Propager les fractionnements en fonction des facteurs

Dans Shardy, nous avons la hiérarchie des tenseurs, des dimensions et des facteurs. Ils représentent des données à différents niveaux. Un facteur est une sous-dimension. Il s'agit d'une hiérarchie interne utilisée dans la propagation du fractionnement. Chaque dimension peut correspondre à un ou plusieurs facteurs. Le mappage entre la dimension et le facteur est défini par OpShardingRule.

Shardy propage les axes de partitionnement le long des facteurs au lieu des dimensions. Pour ce faire, procédez en trois étapes, comme illustré dans la figure ci-dessous.

1. Passer de DimSharding à FactorSharding
2. Propager les axes de fractionnement dans l'espace de FactorSharding
3. Projeter la mise à jour de FactorSharding pour obtenir la mise à jour de DimSharding

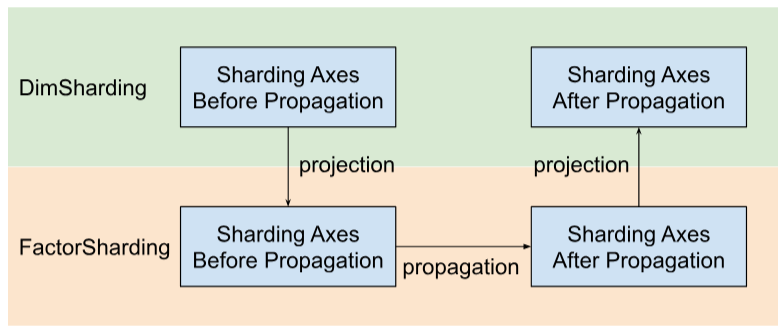
Visualisation de la propagation du fractionnement en fonction de facteurs

Nous utiliserons le tableau suivant pour visualiser le problème et l'algorithme de propagation du sharding.

	F0	F1	F2	Axes répliqués explicitement
T0
T1
T2

• Chaque colonne représente un facteur. F0 signifie le facteur avec l'indice 0. Nous propageons les fractionnements le long des facteurs (colonnes).
• Chaque ligne représente un tenseur. T0 fait référence au tenseur avec l'indice 0. Les tenseurs sont tous les opérandes et les résultats impliqués pour une opération spécifique. Les axes d'une ligne ne peuvent pas se chevaucher. Une axe (ou un sous-axe) ne peut pas être utilisé pour partitionner un tenseur plusieurs fois. Si une axe est répliquée explicitement, nous ne pouvons pas l'utiliser pour partitionner le tenseur.

Ainsi, chaque cellule représente un fractionnement de facteurs. Un facteur peut être manquant dans les tenseurs partiels. Le tableau pour C = dot(A, B) est ci-dessous. Les cellules contenant un N impliquent que le facteur ne figure pas dans le tenseur. Par exemple, F2 se trouve dans T1 et T2, mais pas dans T0.

C = dot(A, B)	Luminosité réduite par traitement par lot F0	F1 : luminosité non contractante	F2 : luminosité non contractante	F3 Luminosité réduite	Axes répliqués explicitement
T0 = A			N
T1 = B		N
T2 = C				N

Collecter et propager les axes de partitionnement

Nous utilisons un exemple simple ci-dessous pour visualiser la propagation.

	F0	F1	F2	Axes répliqués explicitement
T0	"a"		"f"
T1	"a", "b"	"c", "d"	"g"
T2		"c", "e"

Étape 1. Recherchez des axes à propager le long de chaque facteur (ou axes de partitionnement principaux compatibles les plus longs). Pour cet exemple, nous propageons ["a", "b"] le long de F0, ["c"] le long de F1 et rien le long de F2.

Étape 2 : Développez les fractionnements de facteurs pour obtenir le résultat suivant.

	F0	F1	F2	Axes répliqués explicitement
T0	"a", "b"	"c"	"f"
T1	"a", "b"	"c", "d"	"g"
T2	"a", "b"	"c", "e"