Propagación

Descripción general

La propagación del fragmento usa los fragmentos especificados por el usuario para inferir los fragmentos no especificados de tensores (o la dimensión específica de tensores). Recorre el flujo de datos (cadenas de uso-definición) del grafo de procesamiento en ambas direcciones hasta que se alcanza un punto fijo, es decir, el fragmento ya no puede cambiar sin deshacer las decisiones de fragmentación anteriores.

La propagación se puede descomponer en pasos. Cada paso implica analizar una operación específica y propagar entre tensores (operandos y resultados), según las características de esa operación. Tomando un matmul como ejemplo, propagaríamos entre la dimensión no contraída de la izq. o la derecha a la dimensión correspondiente del resultado, o entre la dimensión contraída de la izq. y la derecha.

Las características de una operación determinan la conexión entre las dimensiones correspondientes en sus entradas y salidas, y se pueden abstraer como una regla de fragmentación por operación.

Sin la resolución de conflictos, un paso de propagación simplemente se propagaría tanto como sea posible y, al mismo tiempo, ignoraría los ejes en conflicto. Nos referimos a esto como los ejes de fragmentación principales compatibles (más largos).

Diseño detallado

Jerarquía de resolución de conflictos

Componemos varias estrategias de resolución de conflictos en una jerarquía:

  1. Prioridades definidas por el usuario: En Representación del fragmentación, describimos cómo se pueden adjuntar prioridades a los fragmentamientos de dimensión para permitir el particionamiento incremental del programa, p.ej., hacer paralelismo por lotes -> megatron -> fragmentación de ZeRO. Esto se logra aplicando la propagación en iteraciones. En la iteración i, propagamos todos los particionamientos de dimensiones que tienen prioridad <=i y omitimos todos los demás. También nos aseguramos de que la propagación no anule los particionamientos definidos por el usuario con una prioridad más baja (>i), incluso si se ignoran durante iteraciones anteriores.
  2. Prioridades basadas en operaciones: Propagamos los particionamientos según el tipo de operación. Las operaciones de “transferencia” (p.ej., operaciones por elemento y cambio de forma) tienen la prioridad más alta, mientras que las operaciones con transformación de forma (p.ej., punto y reducción) tienen una prioridad menor.
  3. Propagación agresiva. Propaga los particionados con una estrategia agresiva. La estrategia básica solo propaga particiones sin conflictos, mientras que la estrategia agresiva resuelve los conflictos. Una mayor agresividad puede reducir el uso de memoria a costa de una posible comunicación.
  4. Propagación básica. Es la estrategia de propagación más baja en la jerarquía, que no resuelve ningún conflicto y, en su lugar, propaga ejes que son compatibles entre todos los operandos y resultados.

Jerarquía de propagación, que muestra 4 pilas, de abajo hacia arriba, con las siguientes etiquetas: propagación básica, propagación agresiva, propagación de prioridad de operación y propagación de prioridad del usuario.

Esta jerarquía se puede interpretar como bucles for anidados. Por ejemplo, para cada prioridad del usuario, se aplica una propagación de prioridad de operación completa.

Regla de fragmentación de operaciones

La regla de fragmentación introduce una abstracción de cada operación que proporciona al algoritmo de propagación real la información que necesita para propagar los fragmentos de operandos a resultados o entre operandos sin tener que razonar sobre tipos de operaciones específicas y sus atributos. Esto es, en esencia, factorizar la lógica específica de la operación y proporcionar una representación compartida (estructura de datos) para todas las operaciones con el único fin de la propagación. En su forma más simple, solo proporciona esta función:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

La regla nos permite escribir el algoritmo de propagación solo una vez de una manera genérica que se basa en esta estructura de datos (OpShardingRule), en lugar de replicar fragmentos de código similares en muchas operaciones, lo que reduce en gran medida la posibilidad de errores o comportamientos incoherentes entre las operaciones.

Volvamos al ejemplo de matmul.

Una codificación que encapsula la información necesaria durante la propagación, es decir, las relaciones entre las dimensiones, se puede escribir en forma de notación einsum:

(i, k), (k, j) -> (i, j)

En esta codificación, cada dimensión se asigna a un solo factor.

Cómo usa la propagación esta asignación: Si una dimensión de un operando o resultado se particiona a lo largo de un eje, la propagación buscará el factor de esa dimensión en esta asignación y particionará otros operandos o resultados a lo largo de su dimensión respectiva con el mismo factor y, potencialmente, también replicará otros operandos o resultados que no tengan ese factor a lo largo de ese eje.

Factores compuestos: Extensión de la regla para los cambios de forma

En muchas operaciones, p.ej., matmul, solo necesitamos asignar cada dimensión a un solo factor. Sin embargo, no es suficiente para cambiar de forma.

La siguiente transformación une dos dimensiones en una:

%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

Aquí, las dimensiones 0 y 1 de la entrada corresponden a la dimensión 0 de la salida. Supongamos que comenzamos por darle factores a la entrada:

(i,j,k) : i=2, j=4, k=32

Puedes ver que, si queremos usar los mismos factores para el resultado, necesitaríamos una sola dimensión para hacer referencia a varios factores:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

Lo mismo se puede hacer si el cambio de forma dividiera una dimensión:

%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>

En este caso,

((ij), k) -> (i,j,k) : i=2, j=4, k=32

La dimensión de tamaño 8 aquí se compone esencialmente de los factores 2 y 4, por lo que llamamos a los factores factores (i,j,k).

Estos factores también pueden funcionar en casos en los que no hay una dimensión completa que corresponda a uno de los factores:

%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Este ejemplo también enfatiza por qué debemos almacenar los tamaños de los factores, ya que no podemos deducirlos fácilmente de las dimensiones correspondientes.

Algoritmo de propagación principal

Cómo propagar particiones a lo largo de factores

En Shardy, tenemos la jerarquía de tensores, dimensiones y factores. Representan datos en diferentes niveles. Un factor es una subdimensión. Es una jerarquía interna que se usa en la propagación del fragmento. Cada dimensión puede corresponder a uno o más factores. OpShardingRule define la asignación entre la dimensión y el factor.

Esquema que muestra el algoritmo de propagación de Shardy.

Shardy propaga los ejes de fragmentación a lo largo de factores en lugar de dimensiones. Para ello, tenemos tres pasos, como se muestra en la siguiente figura:

  1. Proyecto DimSharding a FactorSharding
  2. Cómo propagar ejes de fragmentación en el espacio de FactorSharding
  3. Proyecta el FactorSharding actualizado para obtener el DimSharding actualizado.

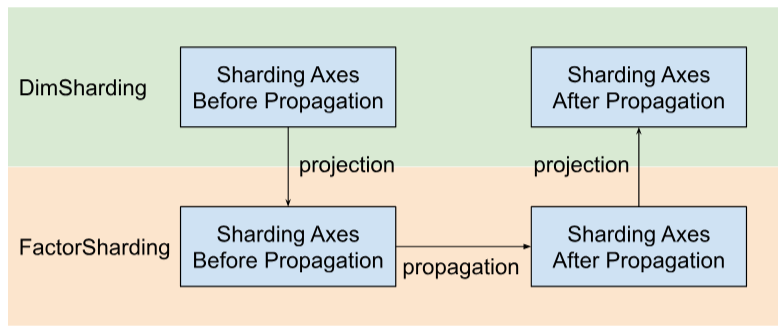
Esquema que muestra la propagación del particionamiento en FactorSharding y DimSharding.

Visualización de la propagación del fragmentación a lo largo de los factores

Usaremos la siguiente tabla para visualizar el problema y el algoritmo de propagación del fragmento.

F0 F1 F2 Ejes replicados de forma explícita
T0
T1
T2
  • Cada columna representa un factor. F0 significa el factor con el índice 0. Propagamos los particionados a lo largo de los factores (columnas).
  • Cada fila representa un tensor. T0 hace referencia al tensor con el índice 0. Los tensores son todos los operandos y resultados involucrados en una operación específica. Los ejes de una fila no se pueden superponer. No se puede usar un eje (o subeje) para particionar un tensor varias veces. Si se replica un eje de forma explícita, no podemos usarlo para particionar el tensor.

Por lo tanto, cada celda representa un fragmento de factor. Puede faltar un factor en los tensores parciales. A continuación, se muestra la tabla de C = dot(A, B). Las celdas que contienen un N implican que el factor no está en el tensor. Por ejemplo, F2 está en T1 y T2, pero no en T0.

C = dot(A, B) Atenuación de agrupación en lotes de F0 Dimensión no contractual de F1 Atenuación no contractante F2 Atenuación de contratación de F3 Ejes replicados de forma explícita
T0 = A N
T1 = B N
T2 = C N

Recopila y propaga los ejes de fragmentación

Usamos un ejemplo simple que se muestra a continuación para visualizar la propagación.

F0 F1 F2 Ejes replicados de forma explícita
T0 "a" "f"
T1 "a", "b" "c", "d" "g"
T2 "c", "e"

Paso 1. Encuentra ejes para propagarse a lo largo de cada factor (también conocidos como los ejes de fragmentación principales compatibles [más largos]). En este ejemplo, propagamos ["a", "b"] a lo largo de F0, propagamos ["c"] a lo largo de F1 y no propagamos nada a lo largo de F2.

Paso 2. Expande los particionamientos de factores para obtener el siguiente resultado.

F0 F1 F2 Ejes replicados de forma explícita
T0 "a", "b" "c" "f"
T1 "a", "b" "c", "d" "g"
T2 "a", "b" "c", "e"

Operaciones de flujo de datos

La descripción del paso de propagación anterior se aplica a la mayoría de las operaciones. Sin embargo, hay casos en los que una regla de fragmentación no es apropiada. En esos casos, Shardy define las operaciones de flujo de datos.

Un borde de flujo de datos de alguna operación X define un puente entre un conjunto de fuentes y un conjunto de destinos, de modo que todas las fuentes y los destinos se deben particionar de la misma manera. Algunos ejemplos de estas operaciones son stablehlo::OptimizationBarrierOp, stablehlo::WhileOp, stablehlo::CaseOp y también sdy::ManualComputationOp. En última instancia, cualquier operación que implemente ShardableDataFlowOpInterface se considera una operación de flujo de datos.

Una operación puede tener varios bordes de flujo de datos que son ortogonales entre sí. Por ejemplo:

    y_0, ..., y_n = while (x_0, ..., x_n)
                    ((pred_arg_0,... , pred_arg_n) { ... })
                    ((body_arg_0,..., body_arg_n) {
                    ...
                    return return_value_0, ..., return_value_n
                    })

Esta operación while tiene n aristas de flujo de datos: las aristas de flujo de datos en el paso i están entre las fuentes x_i, return_value_i y los destinos y_i, pred_arg_i, body_arg_i.

Shardy propagará los particionados entre todas las fuentes y los destinos de un borde de flujo de datos como si fuera una operación normal con las fuentes como operandos y los destinos como resultados, y una identidad sdy.op_sharding_rule. Eso significa que la propagación hacia adelante es de las fuentes a los destinos y la propagación hacia atrás es de los destinos a las fuentes.

El usuario debe implementar varios métodos que describan cómo obtener las fuentes y los destinos de cada borde de flujo de datos a través de su propietario y también cómo obtener y configurar los fragmentos de los propietarios de los bordes. Un propietario es un objetivo especificado por el usuario del borde de flujo de datos que usa la propagación de Shardy. El usuario puede elegirlo de forma arbitraria, pero debe ser estático.

Por ejemplo, dado el custom_op que se define a continuación:

  y_1, ..., y_n = custom_op (x_1, ..., x_n)
                  ((body_arg_1,..., body_arg_n) {
                    ...
                    return return_value_1, ..., return_value_n
                  })

Esta custom_op tiene dos tipos de aristas de flujo de datos: n aristas entre return_value_i (fuentes) y y_i (destinos) y n aristas entre x_i (fuentes) y body_arg_i (destinos). En este caso, los propietarios de los bordes son los mismos que los objetivos.